компьютерные методы. СРС2 Компьютерные методы. Срс моделирование магнитного поля
 Скачать 1.21 Mb.
|
|
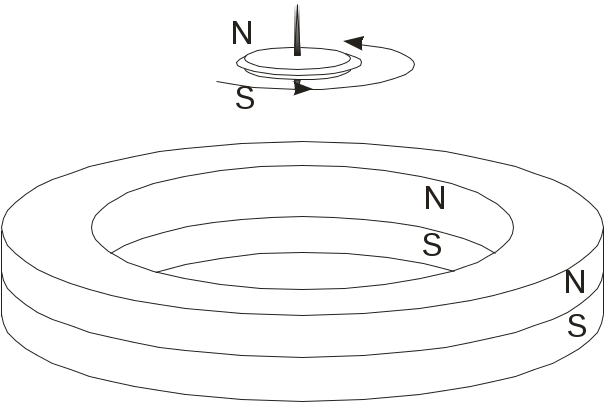 а |  б |
Рисунок 3. Левитрон и его схема
На рисунке 3(а) показан «левитрон», на рисунке 3(б) дано его схематическое изображение. Левитрон представляет собой магнит-волчок массой 22 г., вращающийся над постоянным магнитом-основанием в течение более 2 минут, пока его вращение под действием трения о воздух не замедлится до частоты 1000 радиан в секунду. В работах [6,7] объясняется механизм устойчивого равновесия при некоторых упрощающих предположениях. Элементы теории гироскопов, необходимые для понимания принципа работы левитрона даны в Приложении А.
В 1840 году англичанин Ирншоу обосновал принцип неустойчивости неуправляемой магнитной системы из статических магнитных диполей [8]. Но ученый тогда не знал о таких материалах, как диамагнетики, которые намагничиваются в направлении противоположном внешнему магнитному полю. Именно с их помощью немецкий физик Браунбек осуществил магнитную левитацию и предсказал усиление этого эффекта для сверхпроводников. Прогноз основывался на том, что сверхпроводник проявляет свойства идеального магнитного зеркала – выталкивает из себя силовые линии магнитного поля (эффект Мейснера – Окснфельда) [9].
Левитация по принципу Браунбека впервые на практике была осуществлена в 1945 году П.Капицей по схеме, предложенной В.Аркадьевым («гроб Магомета»). Особенную популярность этот опыт приобрел в последнее время в связи с открытием высокотемпературных сверхпроводников – керамический образец, охлажденный в жидком азоте, может некоторое время, пока он сохраняет свойство сверхпроводимости, парить над постоянным магнитом.
Цель исследования: исследовать численными методами магнитные поля, порожденных различными системами электрических токов и рассмотреть возможности устойчивого равновесия магнитных тел в магнитных полях
Задачи исследования:
Методами численного моделирования при помощи языка программирования FORTRAN построить универсальный алгоритм для определения значения магнитной индукции в любой точке пространства в зависимости от расположения и формы постоянных магнитов или электромагнитов. С помощью разработанного алгоритма построить картину магнитного поля постоянного полосового магнита и электромагнита.
Построить картину магнитного поля кольцевого магнита и электромагнита.
Численными методами определить силы, действующие на пробное магнитное тело, помещенное в магнитные поля различной конфигурации. Исследовать возможности устойчивого равновесия пробного вращающегося магнитного тела в магнитных полях различной конфигурации.
Исследовать возможность равновесия кольцевого проводника в магнитной потенциальной яме.
Теоретическая и практическая значимость: результаты работы можно использовать при проектировании бесконтактных опор различных движущихся систем, при разработке приборов и аппаратов, измерительной аппаратуры, работающей в области действия электромагнитных полей, постановке некоторых физических экспериментов, конструировании устройств для ориентации и транспортировки деталей в промышленности и др.
Левитация предметов в магнитном поле важна для множества практических приложений. Например, выращивание белковых кристаллов, парящих в магнитном поле, позволило устранить разрушительное действие силы тяжести и получить кристаллы невиданных до того размеров 1см.
Делаются попытки скомпенсировать действие силы тяжести при выращивании кристаллов фуллеренов в космосе. Но этот очень дорогой способ не принес столь изящных результатов, которые уже получены в земных условиях методом левитации в магнитном поле.
Неоднородное магнитное поле, создаваемое сверхпроводящими магнитами, открывает новые возможности для управления биологическими объектами, для сепарации нанотрубок и полимеров, для синтеза новых типов материалов и многого другого [10].
Моделирование магнитного поля ПОЛОСОВОГО магнита
Для моделирования магнитного поля полосового магнита заменим его круговым витком с электрическим током. Идентичность этих систем обосновывается совпадением картины их магнитных полей, которая хорошо известна из экспериментов.
Найдем вектор магнитной индукции кругового тока в произвольной точке пространства по закону Био-Савара [11]:
. (1)Пусть радиус кругового витка равен
, сила тока равна 
(рисунок 4). Магнитное поле обладает цилиндрической симметрией, поэтому достаточно найти индукцию 
в точке (x,0,z), где оси Ох и Оу лежат в плоскости витка. Очевидно, что 
. 
Рис. 4
Обозначим:
малый элемент контура, сонаправленный направлению тока . 
, где 
- количество элементов разбиения контура, используемое при численном моделировании. Для расчетов мы положили =1000. Точка витка, в которой начинается вектор 
, имеет координаты 
, где 
, 
. Координаты самого вектора из рисунка равны 
. Тогда вектор, проведенный от элемента тока к точке (x,0,z), имеет координаты
,его модуль равен
.Найдем векторное произведение:
(2)Подставим (2) в (1) и определим координаты вектора магнитной индукции:
(3)
(4)где
. Для приближенного вычисления интегралов (3) и (4), заменим их на суммы Nслагаемых:
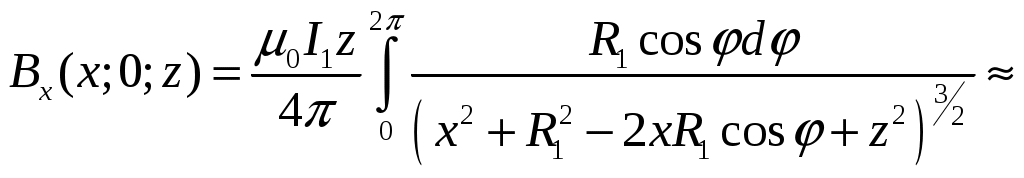
(5)
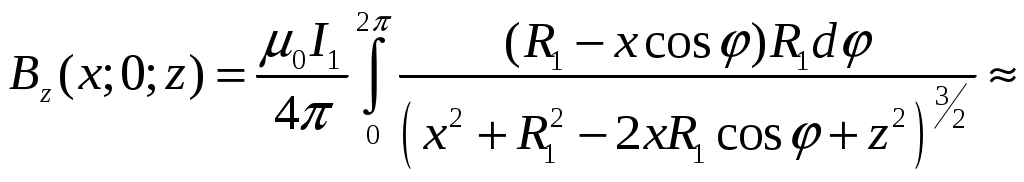
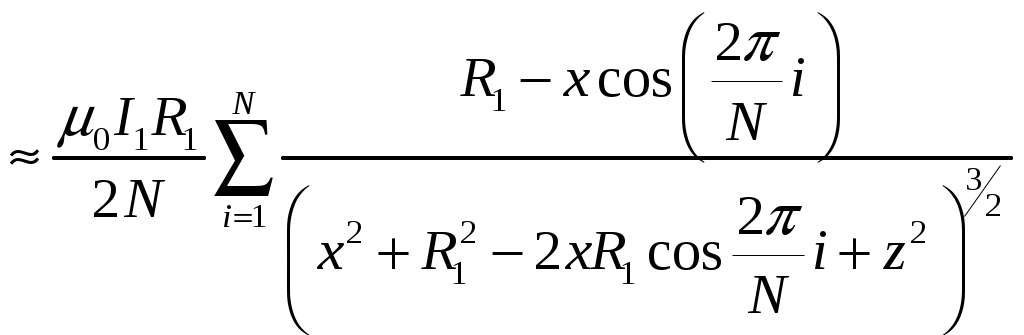. (6)В частности, если x=0, то
,
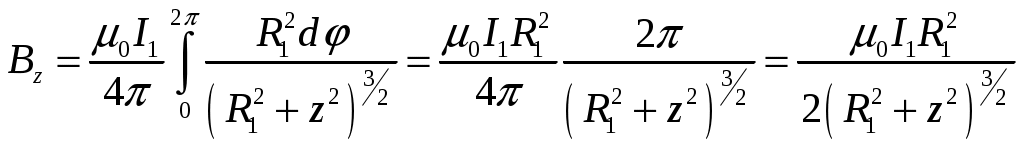,что совпадает с известной формулой для индукции на оси кругового тока [12].
Оценим точность приближенного расчета интегралов (6). Обозначим сумму N слагаемых в (10) как BN. Тогда, согласно [13], получим оценку:
=BN+O(h2), h=
.Положив
=1, получим h=6,28·10-3, и 
4·10-7. (7)Аналогично можно оценить точность расчета по формуле (6).
В программе Sfild1 (см. приложение В) рассчитывается магнитная индукция электрического тока одного витка, радиус которого равен 0,01. Магнитные линии, расположенные в полуплоскости хОz (для х >0) показаны на рисунке 5.
Рисунок 5. Линии магнитной индукции в полуплоскости хОz (для х >0) для кольцевого проводника радиуса 0.01 с центром в точке (0,0,0), лежащего в плоскости хОy; сила тока равна 1 А
Учитывая цилиндрическую симметрию, мы построили магнитные линии во всем пространстве и нашли модуль вектора магнитной индукции в произвольной точке. На рисунке 6 цвет линии характеризует величину модуля вектора индукции: красный – 0.0004 Тл, синий - 0.0001 Тл, сила тока равна 1 А.
Магнитное поле любой конфигурации можно задать как суперпозицию магнитных полей систем различных круговых токов. Поэтому предложенный алгоритм естественным образом обобщается для более сложных магнитных систем.
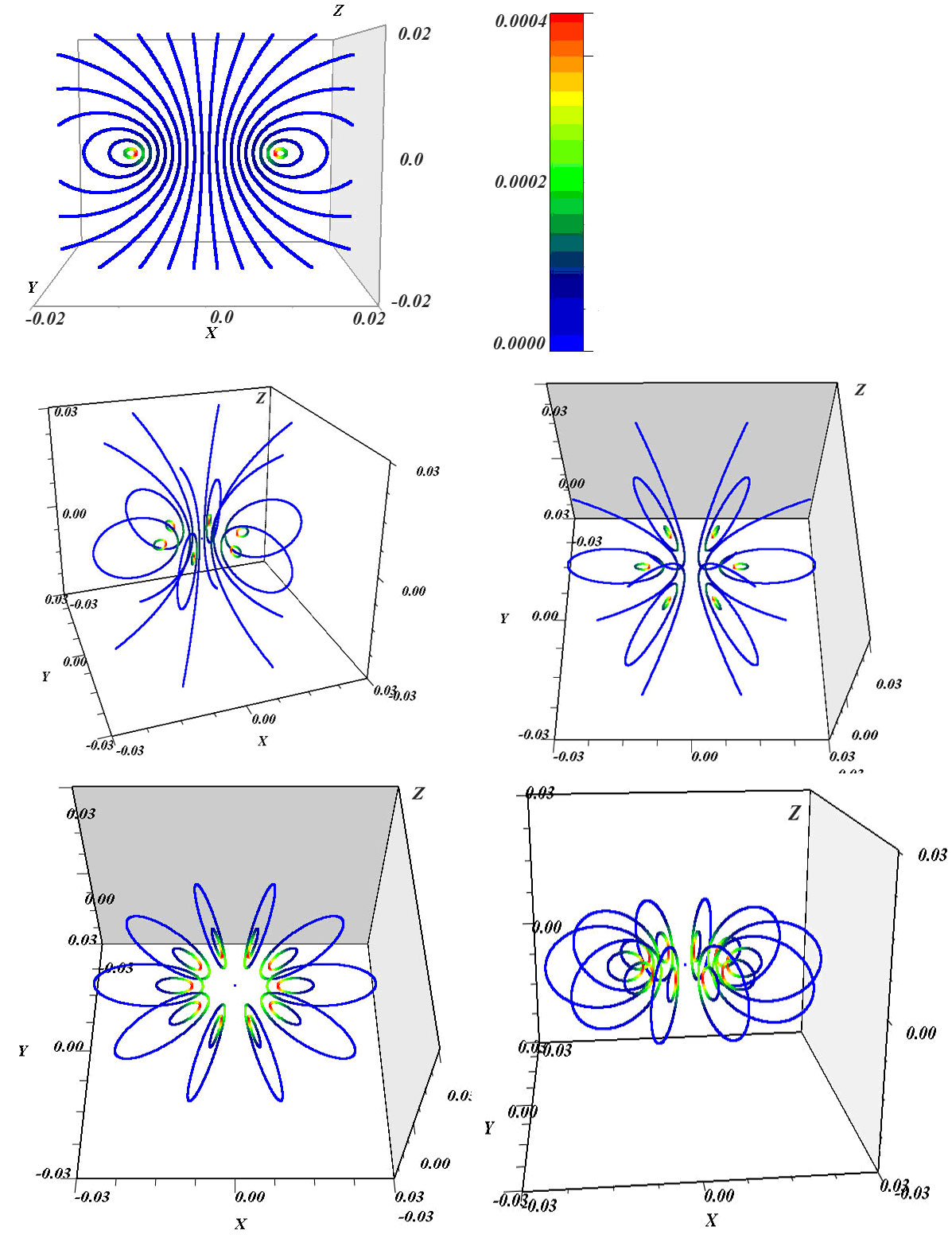
Рисунок 6. Линии магнитной индукции в пространстве для кольцевого проводника радиуса 0.01 с центром в точке (0,0,0), лежащего в плоскости хОу; цвет характеризует величину магнитной индукции; сила тока равна 1 А
Моделирование магнитного поля кольцевого магнита
Для расчетов индукции магнитного поля кольцевого магнита, намагниченного так, как показано на рисунке 7(а), заменим магнит на систему двух разнонаправленных соосных круговых токов, величина каждого из которых равна I(рисунок 7(б)).
Радиусы витков обозначим R1 иR2;пусть для определенности R1 <R2.На оси симметрии токов расположены (симметрично) две точки (назовем их особыми), в которых вектор магнитной индукции обращается в ноль. Найдем их координаты. Направим ось Оzперпендикулярно плоскости витков, начало отсчета поместим в центр витков.
Значение магнитной индукции, созданной каждым током на оси Oz, равно [12]:
, 
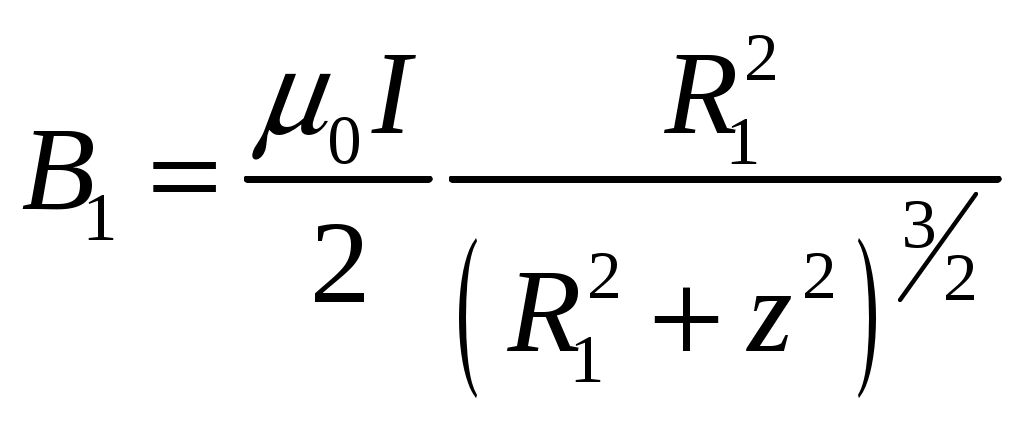, (8)где μ0=4π·10-7 Тл·м/А – магнитная постоянная.
В особых точках
, 
. (9)
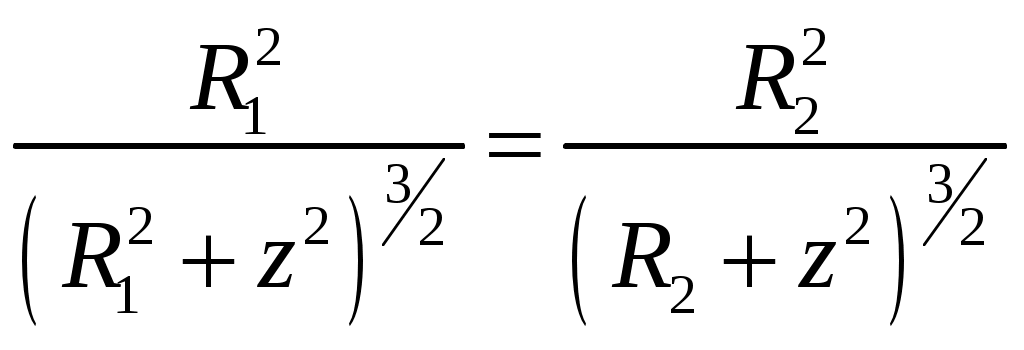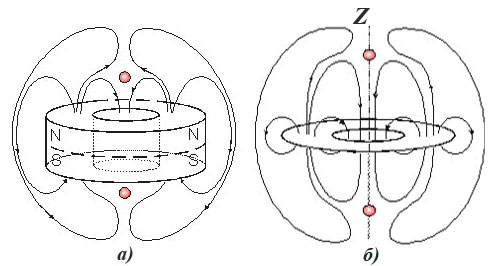
Рисунок 7. Кольцевой магнит и магнитные линии его поля (а); эквивалентная кольцевому магниту система двух круговых токов и магнитные линии (б); красным отмечены особые точки
Поделим обе части уравнения (1) на
, произведем замену 
и обозначим:
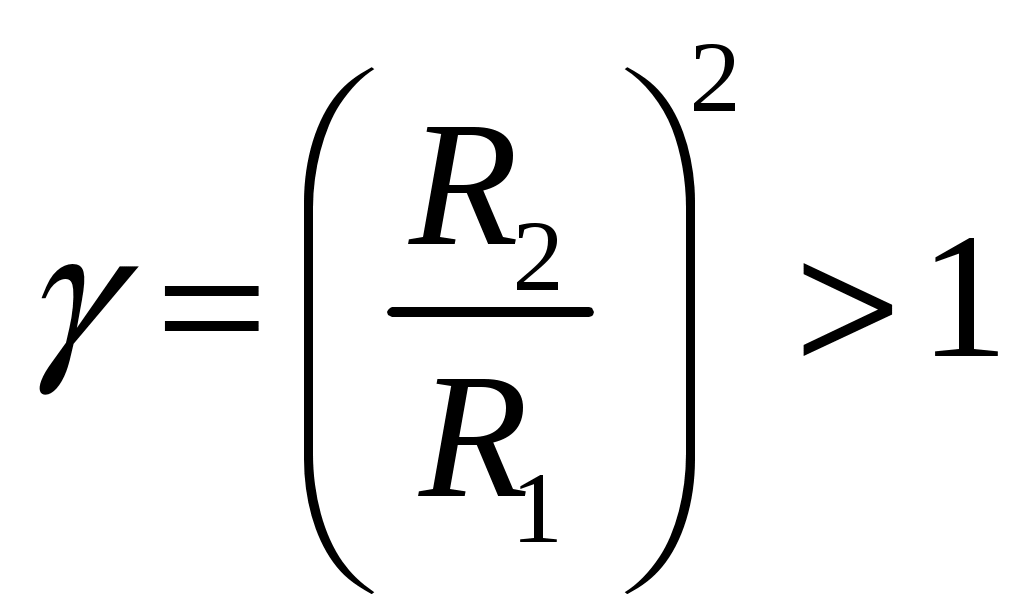. Получим кубическое уравнение
. (10)Решая (10) по методу, изложенному в [14], заменим переменную:
. Получим: 
. Введем новые переменные:
и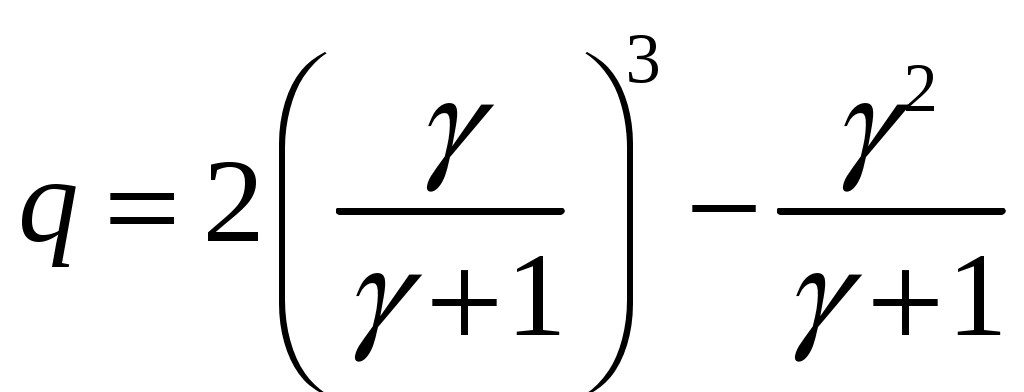 
и рассмотрим выражение 
. (11)Из положительности (11) следует, что кубическое уравнение имеет всего один действительный корень, который найдем по формуле Кардано:
+
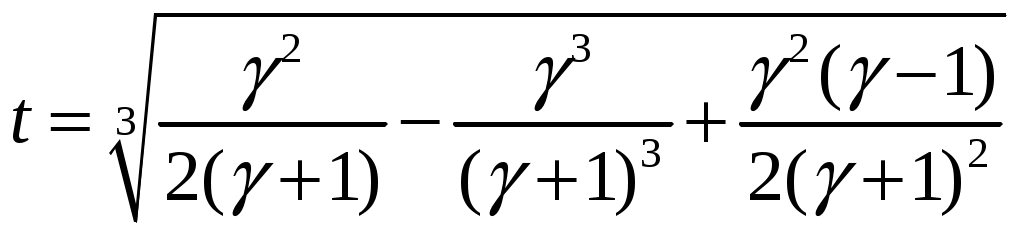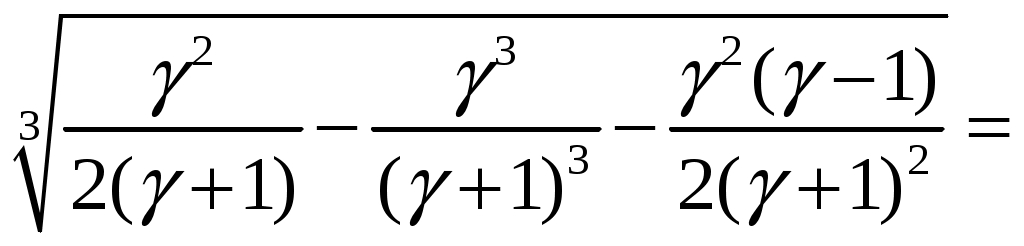
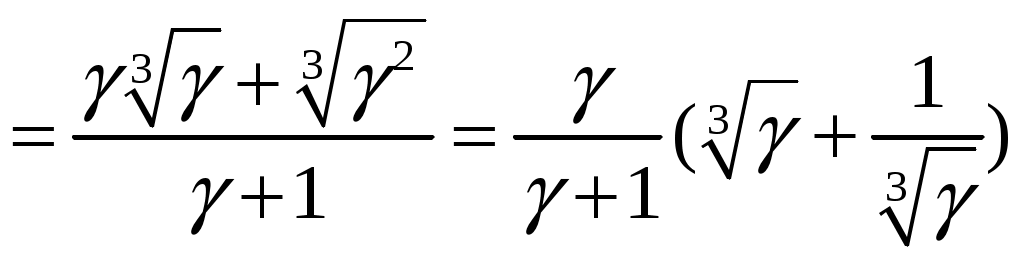.Тогда
, 
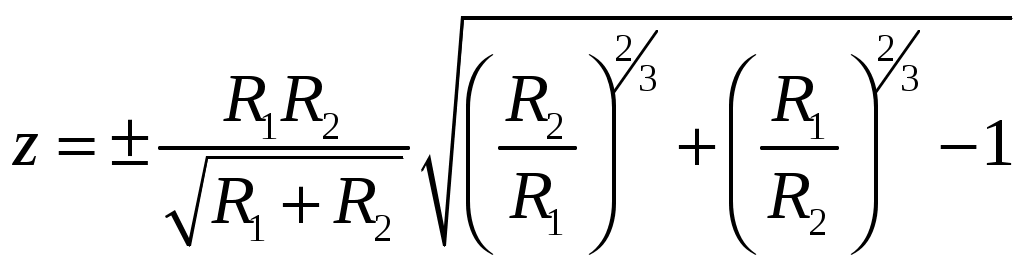. (12)Для систем трех и более круговых соосных токов нахождение координат особых точек сводится к уравнениям 5-й, 7-й и более высоких степеней, поэтому расчет для этих систем мы провели при помощи компьютерного моделирования с использованием языка программирования фортран. Количество особых точек равно N=2n-2, n – количество круговых витков; все особые точки расположены на оси симметрии, причем координаты их, вообще говоря - комплексные.
Рассмотрим второй круговой виток с электрическим током
, причем ток направлен противоположно току . Найдем индукцию поля второго тока в точке 
Рассуждая так же, как при вычислении индукции поля, созданного одним током, получим:
,
.Тогда магнитная индукция поля второго тока
: 
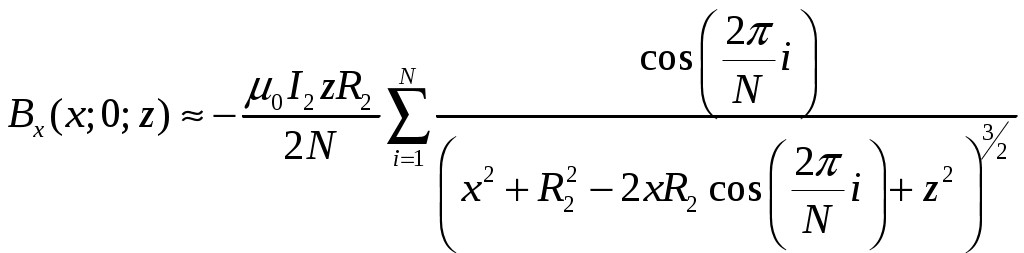, (13)
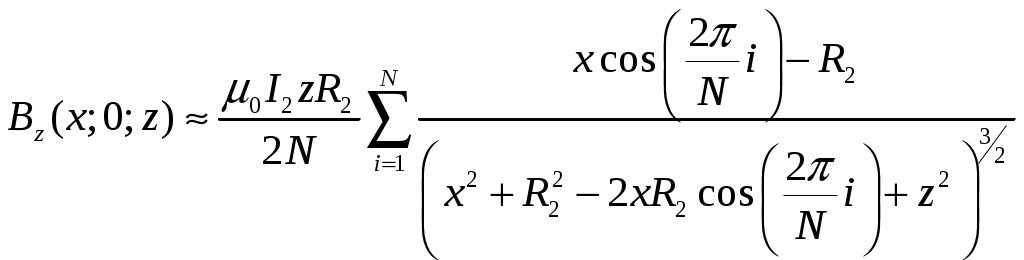. (14)Результирующее поле находим по принципу суперпозиции, складывая соответственно (5), (13) и (6), (14). Точность расчетов, как и в (5-6) имеет порядок 10-7.
На рисунке 8 показаны в правой полуплоскости хОz магнитные линии поля двух разнонаправленных круговых токов: радиусов 0.01 и 0.02, с центрами в точке (0,0,0), сила токов в обоих проводниках 1 А. Особые точки имеют координаты (0,0, ±0.0093).
На рисунке 9 показаны магнитные линии вблизи особой точки. На рисунках 10-11 показаны фрагменты магнитных линий поля двух разнонаправленных токов в пространстве. Все рисунки получены с помощью программы Sfild2 (приложение Г).
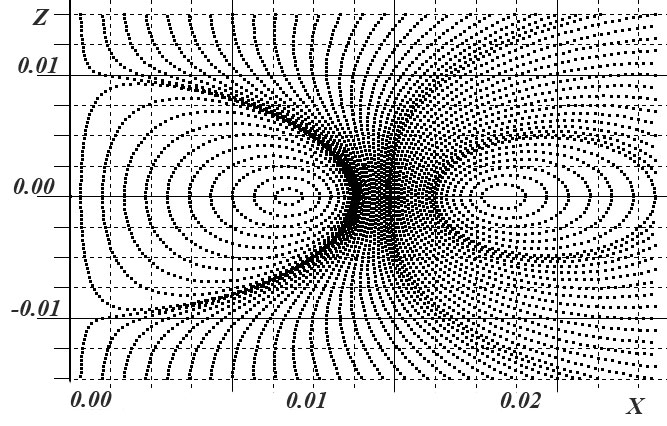
Рисунок 8. Магнитные линии поля двух разнонаправленных токов в полуплоскости хОz
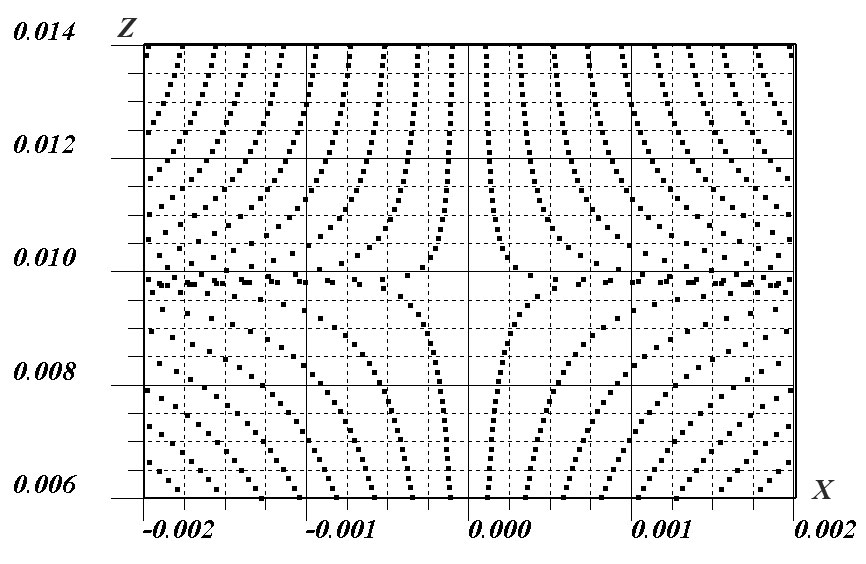
Рисунок 9. Магнитные линии поля двух разнонаправленных токов в полуплоскости хОzвблизи верхней особой точки
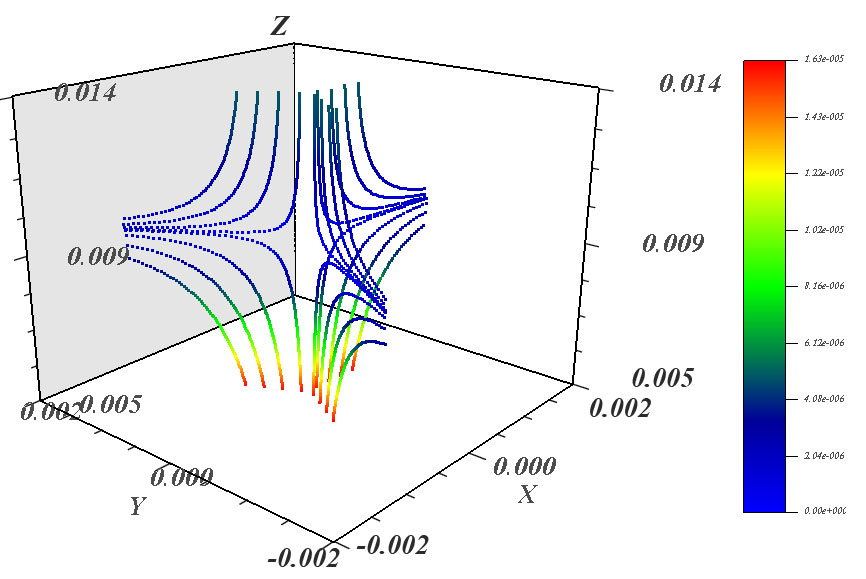
Рисунок 10. Магнитные линии вблизи верхней особой точки в пространстве
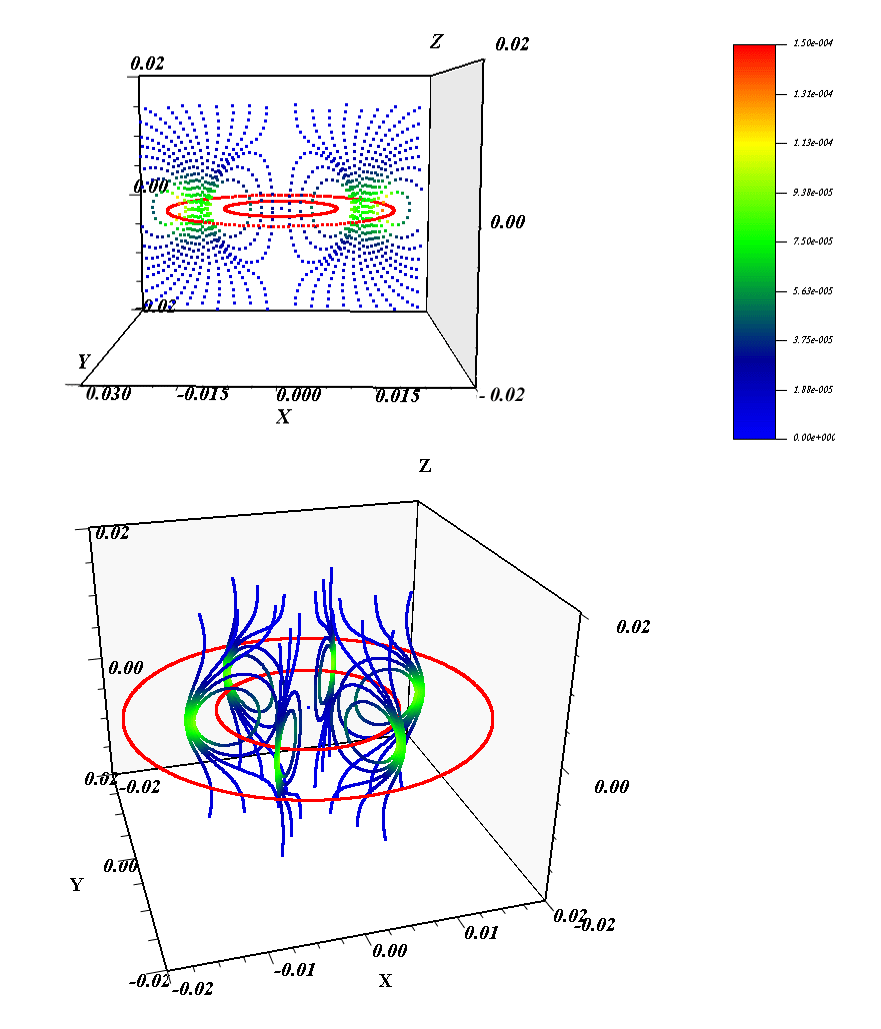
Рисунок 11 (а). Магнитные линии поля двух разнонаправленных токов в пространстве. Цвет характеризует величину магнитной индукции. Два круговых тока показаны красным цветом
Заключение
Изучение движения твердого тела в электрических и магнитных полях стимулируется многочисленными прикладными задачами, возникающими при разработке новых машин и приборов в различных областях современной техники. Такие задачи встречаются при исследовании бесконтактных опор различных движущихся систем, при разработке космических аппаратов, создании измерительной аппаратуры, работающей в области действия электромагнитных полей, постановке некоторых физических экспериментов, конструировании устройств для ориентации и транспортировки деталей в промышленности и др. К разработке неконтактных подвесов проявляется большой интерес как в нашей стране, так и за рубежом. В настоящее время уже созданы отдельные приборы, изготовлены и испытаны различные образцы неконтактных подвесов. Этим успехам в значительной мере способствует прогресс, достигнутый в области механики, электродинамики, теории автоматического регулирования. Вместе с тем с появлением новых приложений постоянно расширяется круг задач, требующих своего решения для рационального конструирования разрабатываемых приборов и машин.
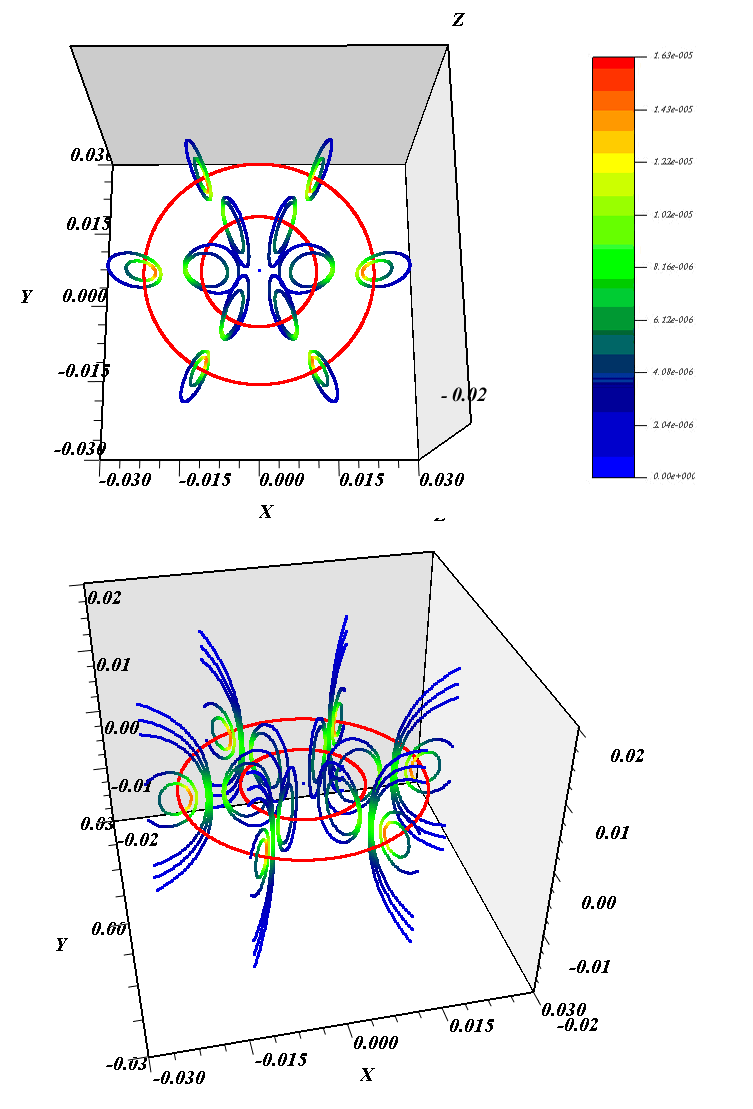
Рисунок 11 (б). Магнитные линии поля двух разнонаправленных токов в пространстве. Цвет характеризует величину магнитной индукции. Два круговых тока показаны красным цветом
Кроме большого прикладного значения, задачи о движении твердого тела в электрических и магнитных полях имеют и принципиальный теоретический интерес.
При движении проводящего твердого тела в электромагнитном поле в теле возникают электрические токи. Возникновение электрических токов приводит, с одной стороны, к тому, что, взаимодействуя с магнитным полем, они вызывают появление сил, которые изменяют движение тела. С другой стороны, возникновение электрических токов приводит к изменению электромагнитного поля. При теоретическом рассмотрении всех этих вопросов необходимо учитывать как механические, так и электродинамические эффекты. Таким образом, возникает задача исследования совместной системы уравнений электродинамики и уравнений движения твердого тела.
Эта проблема, лежащая на стыке классических дисциплин — теоретической механики и электродинамики, в общей постановке является чрезвычайно сложной для аналитического исследования. Поэтому интерес к разработке приближенных способов анализа и расчета движения твердого тела в электромагнитном поле в настоящее время возрастает.
В нашей работе на основе анализа свойств магнитных тел были получены следующие результаты:
Методами численного моделирования при помощи языка программирования FORTRAN построен универсальный алгоритм для определения значения магнитной индукции в любой точке пространства в зависимости от расположения и формы постоянных магнитов или электромагнитов.
2. При помощи этого алгоритма решены задачи численного моделирования:
магнитных полей постоянного полосового магнита и электромагнита;
магнитных полей кольцевого магнита и электромагнита.
В магнитных полях кольцевого магнита и систем двух и более кольцевых соосных токов обнаружены особые точки, в которых индукция магнитного поля обращается в ноль.
Вычислены силы, действующие на пробное магнитное тело, помещенное в магнитные поля различной конфигурации. Исследована возможность устойчивого равновесия пробного вращающегося магнитного тела в магнитных полях различной конфигурации. Обнаружена причина устойчивости равновесия вращающегося пробного магнитного тела в поле кольцевого магнита.
Определена масса тела и период колебаний в магнитной потенциальной яме.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Phys. Rev. 2006. E 65, P. 1-9.
Там же P.10.
D.Kagan. Building a magnetic levitation toy. - Phys. Teach., 31, р. 432-433 (1993).
Ron Edge. Levitation using only permanent magnets. - Phys. Teach., 33, р. 252-253 (1995)
Ron Edge. Corrections to the levitation paper. - Phys. Teach., 34, р. 329 (1996).
M.V.Berry “The Levitron: an adiabatic trap for spin”, Proc. Roy. Soc. London, 452, 1207-1220 (1996).
M.D.Simon. American Journal of Physics, 1997.
Каганов М.И., Цукерник В.М. Природа магнетизма. – М.: Наука, 1982, С. 15.
Савельев И.В. Курс физики. Том 2.- М.: Наука, 1989. С. 267-268.
17. A. L. Migdall, J. V. Prodan, W. D. Phillips, T. H. Bergeman, and H. J. Metcalf, ``First observation of magnetically trapped neutral atoms'', Phys. Rev. Lett., 54, 2596-2599 (2005).
Матвеев А.Н. Электричество и магнетизм. – М.: Высшая школа, 1983, С. 276.
Джанколи Д. Физика.Т 2. - М.: Мир, 1979. С. 205.
Б.П.Демидович, И.А.Марон. Основы вычислительной математики. – М.: Наука, 1966. С.605.
Курош А.Г. Курс высшей алгебры. – М.: Наука, 1975. С. 235-237.
Журнал «Техника – молодежи» №5, 1996 год. С. 9-11.
Мнеян Г.В. Сверхпроводники в современном мире. - М.: Просвещение. С.162.
ПРИЛОЖЕНИЯ
Приложение Б. Программа SFild1
! строит магнитные линию point для одного токф
parameter pi=3.141593, I=1.0, R1=0.01, jmu=pi*4E-07 ! R1=0.01 - диаметр
parameter n=1000,nl=2000, np=10, d=0.0002 ! шаг
! n- число разбиений окружности, nl- количество точек в магнитной линии
! ns - уменьшение для определения шага между точками
real point(nl,2)
real pn(np*nl,4),b(nl)
! real::
common /star1/x,z,bx,bz
const1=jmu*I*R1/(2*n)
k=1
! do ni=1,10
! x=ni*0.001-0.0005; z=0.0
! do ni=1,3
! x=ni*0.003; z=0.0
do ni=1,2
x=(ni-1)*0.002+0.006; z=0.0
do while (z>=0)
point(k,1)=x; point(k,2)=z
call binduction(const1,R1)
b(k)=sqrt(bx**2+bz**2)
x=x+d*bx/b(k); z=z+d*bz/b(k);
k=k+1
! if (x>0.04) exit
! if (z>0.03) exit
if (x>0.04) exit
if (z>0.04) exit
enddo
enddo
print *, 'k1', k
!*********************************************************
! построение трехмерного изображения
do m=i,k
point(k+m,1)=point(m,1)
point(k+m,2)=-point(m,2)
b(k+m)=b(m)
enddo
do j=0,np-1
do m=1,k*2
pn(m+j*k*2,1) = point(m,1)*cos(j*2*pi/np)
pn(m+j*k*2,2) = point(m,1)*sin(j*2*pi/np)
pn(m+j*k*2,3) = point(m,2)
pn(m+j*k*2,4) = b(m)
enddo
enddo
pause
end
!****************************************************
subroutine binduction(const,R)
parameter n=1000, pi=3.141593
common /star1/x,z,bx,bz
bx=0.0; bz=0.0
do j=1,n
co=cos(2*pi*j/n)
denom=sqrt((x**2+R**2+z**2-2*x*R*co)**3)
bx=bx+co/denom; bz=bz+(R-x*co)/denom
enddo
bx=const*z*bx; bz=const*bz
return
end
!***************************************************
Приложение Г. Программа SFild2
! строит магнитные линию point для двух разнонаправленных токов
parameter pi=3.141593, I=1.0, R1=0.01, R2=0.02, jmu=pi*4E-07
parameter n=1000, nl=20000, d=0.00017 ! шаг
! n- число разбиений окружности, nl- количество точек в магнитной линии
! ns - уменьшение для определения шага между точками
real point(nl,2)
real pn(30*nl,4),b(nl)
! real::
common /star1/x,z,bx,bz
z0=sqrt(exp(2*(log(R2/R1))/3)+exp(2*(log(R1/R2))/3)-1.0)
z0=R1*R2*z0/sqrt(R1**2+R2**2)
! z0 - особая точка
print *,z0
! pause
const1=jmu*I*R1/(2*n)
const2=-jmu*I*R2/(2*n)
! нижняя ветвь слева
k=1
do ni=1,10
x=ni*0.001-0.0005; z=0.0
do while (z>=0)
point(k,1)=x; point(k,2)=z
call binduction(const1,R1)
x1=bx; z1=bz
call binduction(const2,R2)
x1=x1+bx; z1=z1+bz; b(k)=sqrt(x1**2+z1**2)
x=x+d*x1/b(k); z=z+d*z1/b(k);
k=k+1
enddo
enddo
print *, 'k1', k
! верхняя ветвь
do ni=1,25
x=ni*0.001-0.0005; z=0.015
do while (z>=0)
point(k,1)=x; point(k,2)=z
call binduction(const1,R1)
x1=bx; z1=bz
call binduction(const2,R2)
x1=x1+bx; z1=z1+bz; b(k)=sqrt(x1**2+z1**2)
x=x+d*x1/b(k); z=z+d*z1/b(k);
k=k+1
enddo
enddo
print *, 'k2', k
! правая ветвь снизу
do ni=1,7
x=ni*0.001+0.02; z=0.0
do while (z>=0)
point(k,1)=x; point(k,2)=z
call binduction(const1,R1)
x1=bx; z1=bz
call binduction(const2,R2)
x1=x1+bx; z1=z1+bz; b(k)=sqrt(x1**2+z1**2)
x=x+d*x1/b(k); z=z+d*z1/b(k);
k=k+1
enddo
enddo
print *, 'k3', k
! правая ветвь
do ni=2,15
x=0.027; z=ni*0.001
do while (z>=0)
point(k,1)=x; point(k,2)=z
call binduction(const1,R1)
x1=bx; z1=bz
call binduction(const2,R2)
x1=x1+bx; z1=z1+bz; b(k)=sqrt(x1**2+z1**2)
x=x+d*x1/b(k); z=z+d*z1/b(k);
k=k+1
enddo
enddo
print *, 'k4', k
continue
!*********************************************************
! построение трехмерного изображения
do m=i,k
point(k+m,1)=point(m,1)
point(k+m,2)=-point(m,2)
b(k+m)=b(m)
enddo
do j=0,0
do m=1,k*2
pn(m+j*k*2,1) = point(m,1)*cos(j*2*pi/30)
pn(m+j*k*2,2) = point(m,1)*sin(j*2*pi/30)
pn(m+j*k*2,3) = point(m,2)
pn(m+j*k*2,4) = b(m)
enddo
enddo
pause
end
!****************************************************
subroutine binduction(const,R)
parameter n=1000, pi=3.141593
common /star1/x,z,bx,bz
bx=0.0; bz=0.0
do j=1,n
co=cos(2*pi*j/n)
denom=sqrt((x**2+R**2+z**2-2*x*R*co)**3)
bx=bx+co/denom; bz=bz+(R-x*co)/denom
enddo
bx=const*z*bx; bz=const*bz
return
end
!***************************************************