роль математики в исскустве. статья по математике. Статья по теме Математика в искусстве
 Скачать 407.45 Kb. Скачать 407.45 Kb.
|
|
Статья по теме: «Математика в искусстве». Казалось бы, что математика и искусство совершенно разные вещи, ведь математика – это наука, исторически основанная на решении задач о количественных и пространственных соотношениях, а искусство - это высокая степень умения и мастерства в любом виде деятельности, но несмотря на все их различия, на самом деле они связаны довольно тесно. А если размышлять над этим вопросом, то математика это и есть своеобразное искусство. Об этом также упоминал великий французский математик А. Пуанкаре: «Математика-это искусство называть разные вещи одним и тем же именем». Её след оставлен практически в каждом направлении человеческого творчества: поэзия, музыка, живопись, музыка, танцы, архитектура, скульптура и др. Искусство помогало создавать и изучать модель мира, а также выявлять его закономерности, в этом ему на помощь и приходит математика. Теперь можем плавно перейти к тому, как же все-таки соотносятся эти два понятия. Архитектура в любое время являлась и продолжает являться одним из самых ярких представителей, совмещающих в себе математику и искусство. Ответим на интересующий всех вопрос, как математика помогает в проектировании и постройке сооружений, а также помогает поддерживать их стойкость и прочность, ведь в древние времена, как только они научились сооружать здания, это стало одной из главных и значимых проблем. Ибо прочность зависит не только от стройматериалов, но и от проектирования конструкции сооружения. В этом нам и помогают математические навыки и то какие знания мы можем применить в строительстве. Интересным примером нам послужат египетские пирамиды, построенные еще далеко до нашей эры. Они имеют форму правильных четырехугольных пирамид. Именно эта геометрическая фигура дает наибольшую устойчивость за счет большой площади соприкосновения с землёй. С другой стороны, форма пирамиды обеспечивает меньшую массу по мере увеличения высоты над поверхностью земли. Благодаря этим двум свойствам пирамида остается устойчивой, а значит и достаточно прочной. Как бы это не звучало странно, но и в танцевальном искусстве математика тоже имеет свое место и немаловажное значение. Поскольку математическая наука связана с понятием алгоритма («шаг за шагом») и последовательностью, а танцевальный шаг - это и последовательность, и порядок движений, то следует, что танец и математика связаны общим понятием - «шагом». Алгоритмы используются для выполнения однотипных задач, чтобы ускорить процесс достижения результата. Суть алгоритма в том, что, научившись выполнять элементарные операции, в дальнейшем мы не задумываемся о порядке их выполнения. Как и в математике, танец имеет свой набор аспектов, которые необходимо освоить в первые годы обучения, чтобы довести их до автоматизма. «Математика не менее поэтична и красива, чем литература». Ведь у них есть как минимум три общих черты: использование математических деталей, понятий и задач; сходство математических и литературоведческих терминов. В качестве примера, можно вспомнить великого математика, как Омар Хайям, который мало того, что являлся математиком, отличился еще и своим поэтическим навыком, в своих стихах он воспевал свободу В скульптуре математика играет также не самую последнюю роль, а одну из главных. Ведь вся суть заключается в составлении пропорций. Как известно, что еще в древние времена основу скульптуры составляла такая теория, как «теория пропорций». Отношения частей человеческого тела связывали с формулой золотого сечения. Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему a : b = b : c или с : b = b : а. Отрезок прямой АВ можно разделить точкой C на две части следующими способами: на две равные части АВ : АC = АВ : ВC; на две неравные части в любом отношении (такие части пропорции не образуют); таким образом, когда АВ : АC = АC : ВC. Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении. 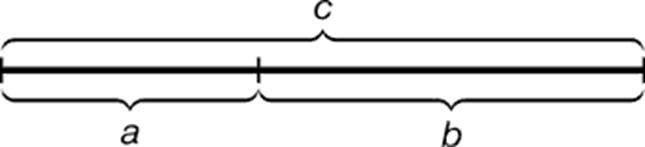 Великий древнегреческий скульптор Фидий довольно таки часто использовал «золотое сечение» в своих работах. Так, например, данные следы сечения можно заметить в статуях Зевса Олимпийского и Афины Парфенос. Жолтовский же, с свою очередь ввел в теорию архитектуры «функцию золотого сечения» (отношение 0,528 к 0,472). Тем самым, используя золотое сечение и его функции, мастер и его ученики создали немало прекрасно спропорционированных композиций, в том числе был и Ривьерский мост через реку Сочи.  Рассуждая о «золотом сечении» в архитектуре хочется закончить примером пропорционального строя храма Василия Блаженного в Москве. За «целое» a=1, принята высота храма. Пропорции храма определяются восьмью членами ряда золотого сечения. Многие из членов ряда неоднократно повторяются в пропорциях этого сооружения, но благодаря адаптивному свойству золотого сечения мы можем быть полностью уверены, что все части сойдутся в целое. Таким образом, адаптивное свойство золотого сечения делает эту геометрическую пропорцию единственной и не повторимой.  Так же, одним из ярких примеров использования математики в искусстве может стать живопись. Ведь абсолютно все в нашем мире состоит и геометрических фигур: круг, овал, квадрат и так далее. Используя их, мы добьемся четких и ровных очертаний предметов или силуэтов людей. Прорисовывая поверх фигур желаемую картину, при этом не ошибаясь в пропорциях задуманной идеи. В 1509 году в Италии в свет вышла книга Луки Пачоли «О божественной пропорции». В ней автор устанавливает математические соотношения, соблюдая которые художник достигает красоты, когда создает свое произведение. Ровно также, как и в других видах искусства математика представлена и в музыке. Это также подчеркнул немецкий философ Г. Лейбниц: «Музыка есть таинственная арифметика души; Она вычисляет, сама того не подозревая». Так получается, что музыка не может существовать без математики. Без каких либо, даже базовых знаний математики невозможно сыграть мелодию или услышать высокий и низкий звук, протяжное и отрывистое звучание. Главной основой математических знаний является арифметический счет. Счет, как числовой ряд, состоит из определенной последовательности чисел, в которой каждое последующее число больше предыдущего на одну единицу – и это уже само по себе является определенной ритмической закономерностью. Также математика пригождается в записи нотных записей и для доли такта. Доля такта – это единица метра музыкального размера. Доли такта представляют собой малые отрезки одинаковой длительности, из которых складывается текст. Величина доли такта указывается в знаменателе дроби, обозначающей размер: например, в размере 3/4 – долей такта является четвертная нота, в размере 2/2 – половинная, в размере 3/8 – восьмая. Числитель дроби указывает количество долей в такте. Также, можем обратиться к мнению и высказываниям великих людей. Многие из них согласны, что математика является неотъемлемой частью искусства, а другие напротив заявляют о том, что наука не играет абсолютно никакой роли. Такой великий человек, итальянский художник и учёный, а также изобретатель, писатель, музыкант, один из крупнейших представителей искусства эпохи Высокого Возрождения – Леонардо да Винчи, который был убежден в единстве математики и живописи. Однажды он сказал: «Пусть никто, не будучи математиком, не дерзнет читать мои труды». Сферой его изучения являлись пропорции. В одном из его известнейших рисунков под названием «Витрувианский человек» изображена идеальная пропорция тела человека, которая заключена в соотношении стороны квадрата и радиуса окружности. Еще одна идеальная пропорция тела была сформулирована еще во времена Древней Греции: Рост человека=размаху рук (от кончиков пальцев) =8 ладоням=6 ступням=8лицам. Леонардо да Винчи (1452-1519) ввел такой немаловажный для художников термин как "Золотое сечение". Композиция портрета "Джоконда" основана, по словам Луки Пачиоли (средневекового монаха), на золотых треугольниках, которые являются частями звездчатого пятиугольника. Золотой треугольник выглядел так и имел следующую формулу:  Позицию по поводу связи математики и искусства Леонардо да Винчи можно проследить в его высказывании: " Пусть не читает меня тот, кто не математик". Объяснить его позицию довольно просто: многие его работы написаны при помощи использования математических формул и геометрических фигур. Исходя из этого, изучая дневники Леонардо, мы наблюдаем картину того, что человек, посещавший самую обычную школу и самостоятельно с помощью своего друга Луки Пачоли изучавший математику в 40 лет, свободно оперировал понятиями высшей математики. Леонардо подошел к понятию предела, начал дифференциального и интегрального исчисления. То, о чем он писал в своих дневниках, – это те основы, опираясь на которые делали свои открытия Ньютон и Лейбниц. Также и Франсуа Морелле постоянно вдохновлялся математикой и геометрией в своей работе. Таким образом, можно сделать вывод о том, что все великие произведения искусства построены на математических законах. На памяти людей нет ни одного красивейшего творения рук человека, ни одного архитектурного или творческого сооружения, музыкального или литературного произведения, которое было бы создано без использования математических знаний и формул. Каждое из таких произведений включает в себя навыки и умения использования математики. То есть, если бы все великие художники, архитекторы, музыканты и т.д. не и если бы знаний в области математики то, как я считаю, они бы не смогли создать столько великих произведений искусства, которыми мы можем наслаждаться по сей день. Если бы никто из них не знал математику, мир бы не познал таких произведений как, например, Пизанская башня, которая находится в наклоненном положении, но все равно твердо стоит на поверхности земли, более девяти сотен лет и продолжает радовать нас своим видом по сей день. |
