ргр 19. Статический анализ точности геометрических параметров в строительстве

• Название: Статический анализ точности геометрических параметров в строительстве
• Дата: 20.01.2019
• Размер: 0.67 Mb.
• Имя файла: ргр 19.doc
• Тип: Анализ; #64392
• страница: 2 из 3

Январь	411=411+2*(-19)+38
Февраль	325=305+2*(-9)+38
Март	557=557+2*(-19)+38
Апрель	266=284+2*(-28)+38
Май	474=428+2*4+38

По формулам определяем статистические характеристики xm и Sx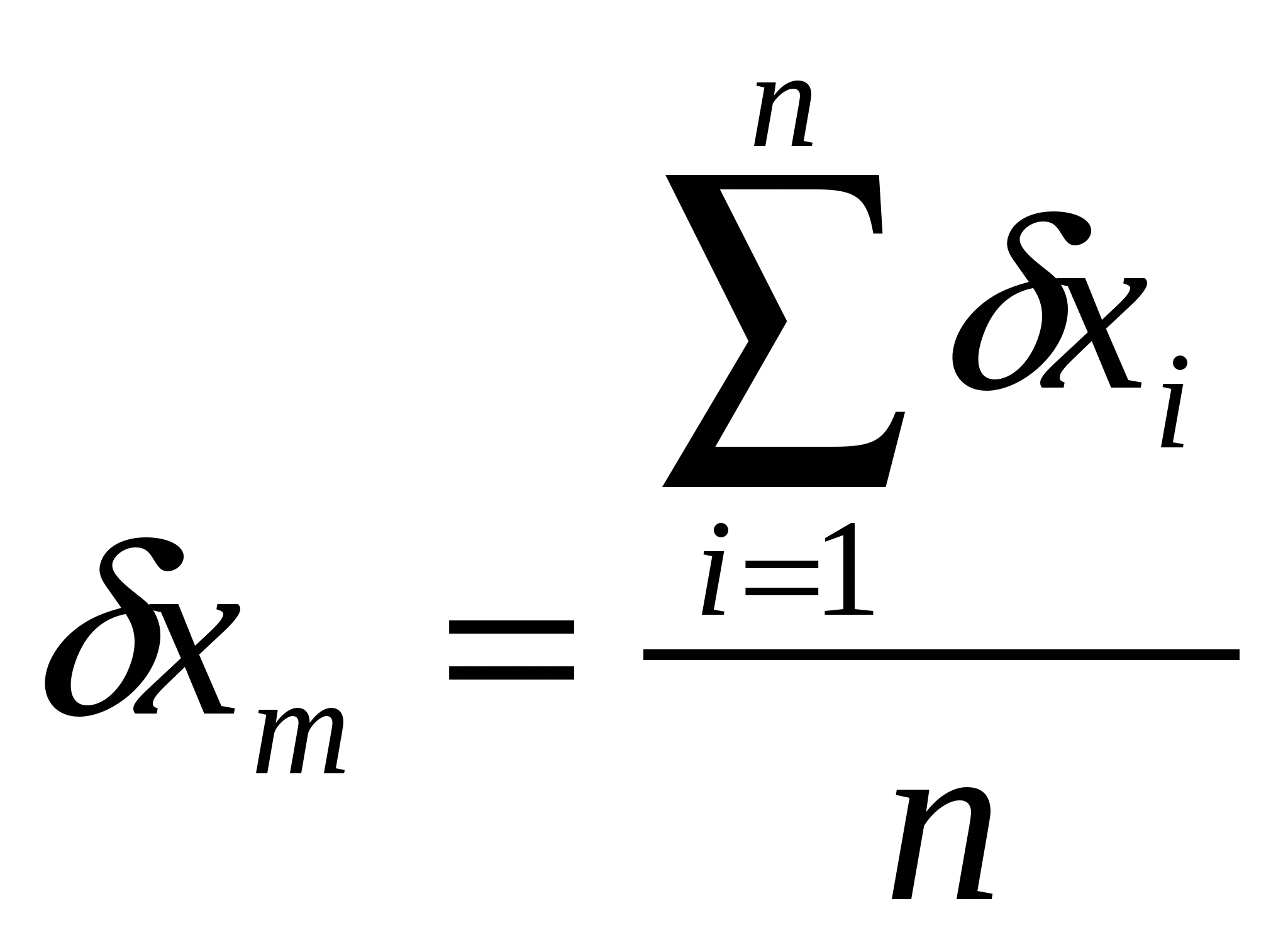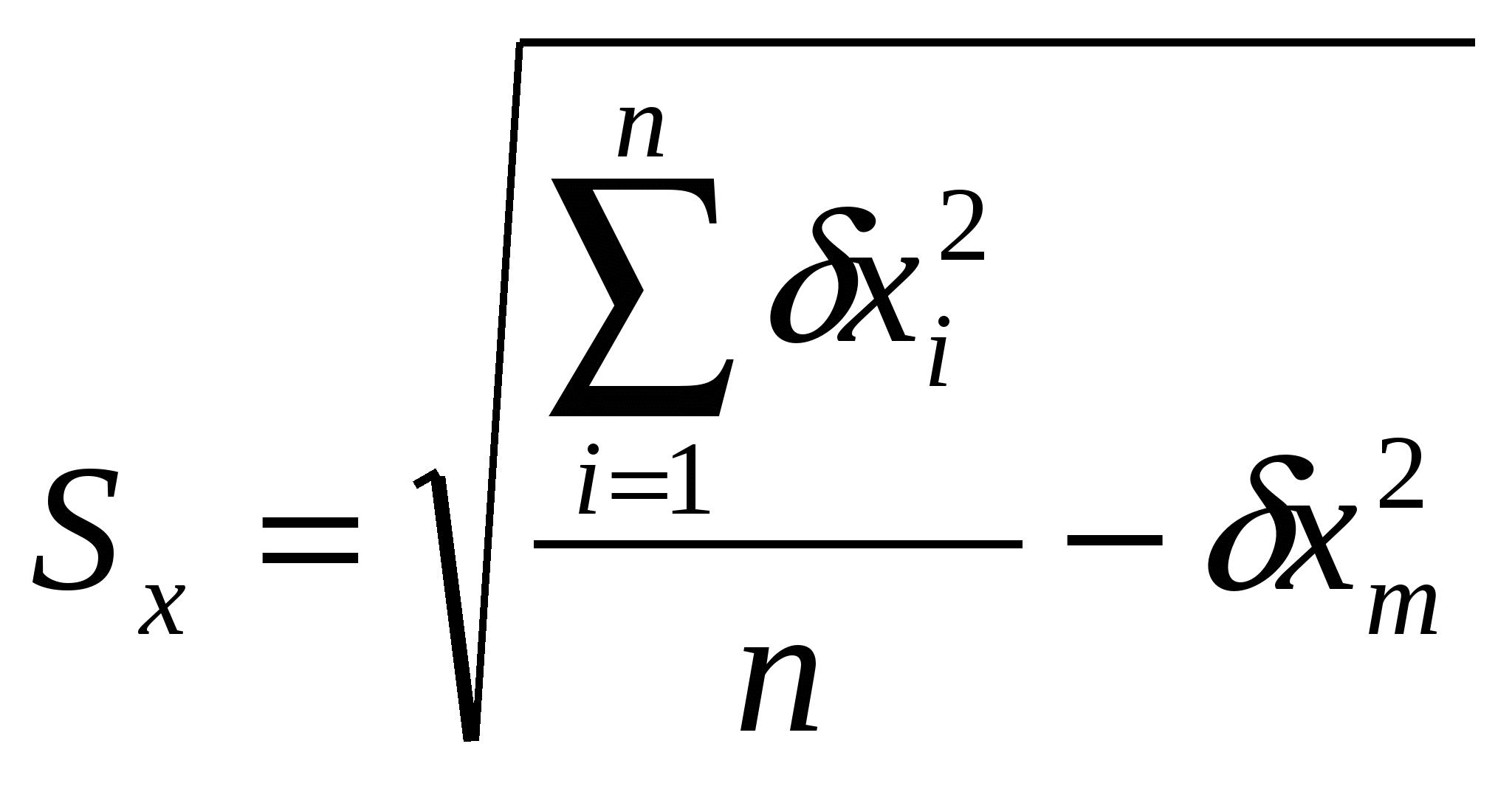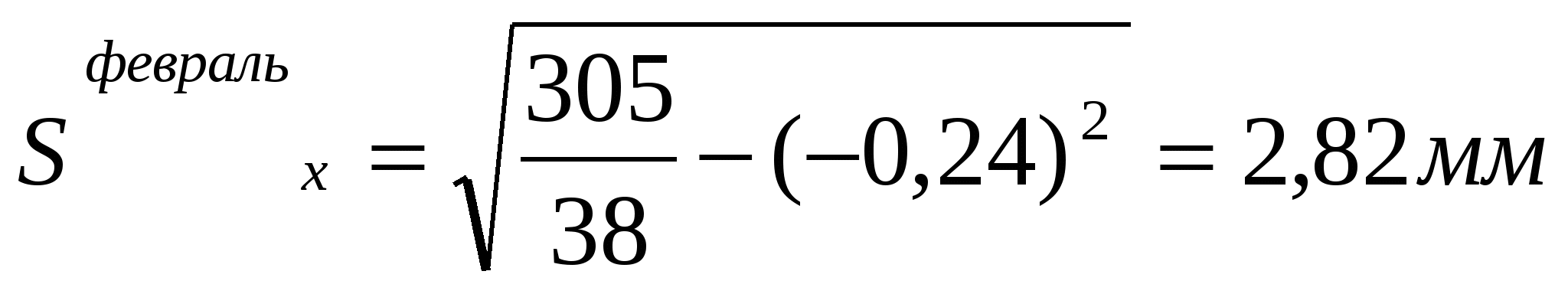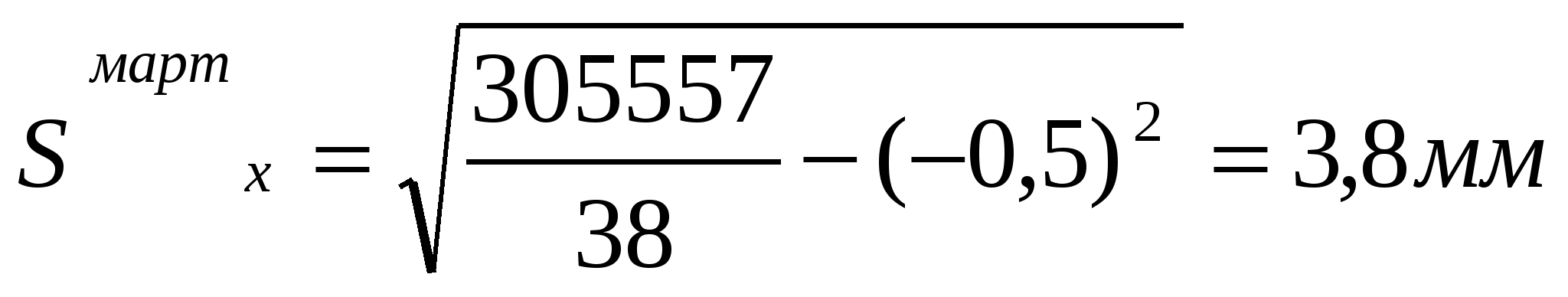











2. В течение последующих трех месяцев в аналогичном порядке были образованы еще три выборки того же объема n = 38, для каждой из которых вычисляем те же статистические характеристики xm и Sx.

Результаты вычислений статистических характеристик по всем выборкам приведены в табл.2.
Таблица 2. Результаты вычислений статистических характеристик по всем выборкам.

№ п/п	Месяц,год	n	xm, мм	Sx, мм
1	01.2014	38	-0,5	3,25
2	02.2014	38	-0,24	2,82
3	03.2014	38	-0,5	3,8
4	04.2014	38	-0,74	2,63
5	05.2014	38	0,105	3,35
		Σn= 190

3. Из действительных отклонений во всех выборках выбираем наибольшее xjmax = +5 мм и наименьшее xjmin = -5 мм значения.

Поле рассеяния между ними разделим на интервалы шагом
.
Округляем расстояние h до целого значения: h=1 мм.

Тогда количество интервалов расстоянием в 1 мм будет равно 12 с границами, равными -5,5; -4,5; -3,5; -2,5; -1,5; -0,5; 0,5; 1,5; 2,5; 3,5; 4,5; 5,5мм:
а1 = xmin – h/2= –5–1/2= -5,5 мм;

а2 = а1+ h= -5,5+1= -4,5 мм;

а3 = а2+ h= – 4,5+1=-3,5мм;

а4 = а3+ h= –3,5+1=-2,5 мм;

а5 = а4+ h= -2,5+1= -1,5 мм;

а6 = а5+ h= -1,5+1=-0,5 мм;

а7 = а6+ h= -0,5+1=0,5 мм;

а8 = а7+ h= 0,5+1= 1,5 мм;

а9 = а8+ h= 1,5+1= 2,5 мм;

а10 = а9+ h= 2,5+1= 3,5 мм;

а11 = а10+ h= 3,5+1= 4,5 мм;

а12 = а11+ h= 4,5+1= 5,5 мм;
Рассчитаем центры интервалов и выразим их целыми числами. Определим частоты попадания результатов измерений в каждый интервал.
Таблица 3. Результаты вычислений статистических характеристик по всем выборкам

Интервал, мм	Частота появления действительных отклонений fj	Центр интервала, мм
-5,5…-4,5	22	-5
-4,5…-3,5	19	-4
-3,5…-2,5	18	-3
-2,5…-1,5	20	-2
-1,5…-0,5	24	-1
-0,5…0,5	11	0
0,5…1,5	14	1
1,5…2,5	15	2
2,5…3,5	15	3
3,5…4,5	16	4
4,5…5,5	16	5

Заносим полученные результаты в графу 2 табл. 3.1 и строим гистограмму действительных отклонений результатов измерений (табл.3.1).

Распределим действительные отклонения xj из всех выборок по интервалам, после чего подсчитаем количество отклонений в каждом интервале (частоты). Далее строим гистограмму и выполняем все промежуточные вычисления в таблице. Правильность заполнения таблицы проверяем тождеством
;
2033=1985+2*(-71)+190

2033=1985+(-142)+190

2033=2033
Таблица 3.1. Гистограмма действительных отклонений и таблица расчета статистических характеристик

Харак-терные точки норма-льной кривой	Центры интерваловхi	Частота появления действительных отклонений											fj	хi2	хi  	(хi + 1)2	fj хi	fj хi2	fj (хi + 1)2
1	2	3											4	5	6	7	8	9	10
		0	5	10	15	20	25	30	35	40	45	50
-10 -6,8 -3,6 -0,4 2,8 6 9,2
	-10
	-9
	-8
	-7
	-6
	-5												22	25	-4	16	-110	550	352
	-4												19	16	-3	9	-76	304	171
	-3												18	9	-2	4	-54	162	72
	-2												20	4	-1	1	-40	80	20
	-1												24	1	0	0	-24	24	0
	0												11	0	1	1	0	0	11
	1												14	1	2	4	14	14	56
	2												15	4	3	9	30	60	135
	3												15	9	4	16	45	135	240
	4												16	16	5	25	64	256	400
	5												16	25	6	36	80	400	576
	6
	7
	8
	9
Сумма													190	-	-	-	-71	1985	2033