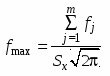ргр 19. Статический анализ точности геометрических параметров в строительстве
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
|
Характеристики xm и Sx вычисляем по формулам (6а) и (7а): 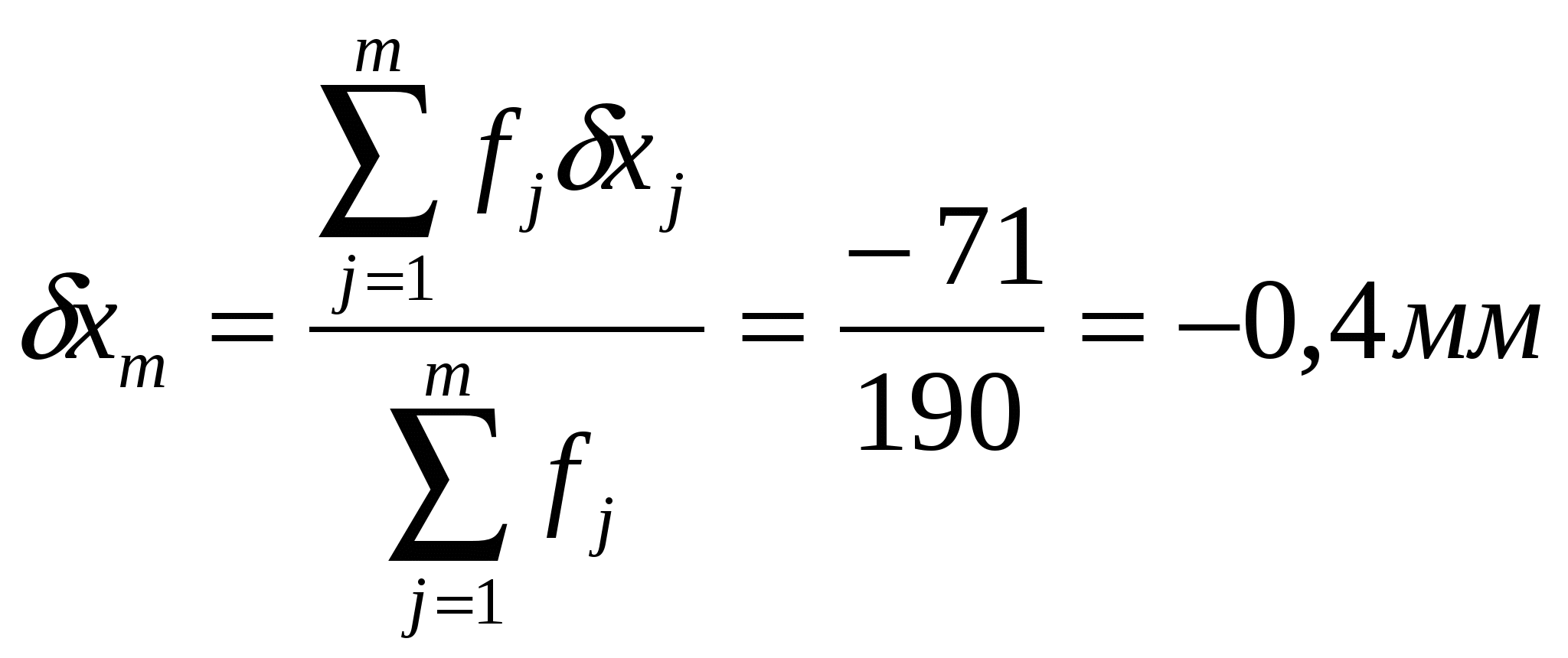 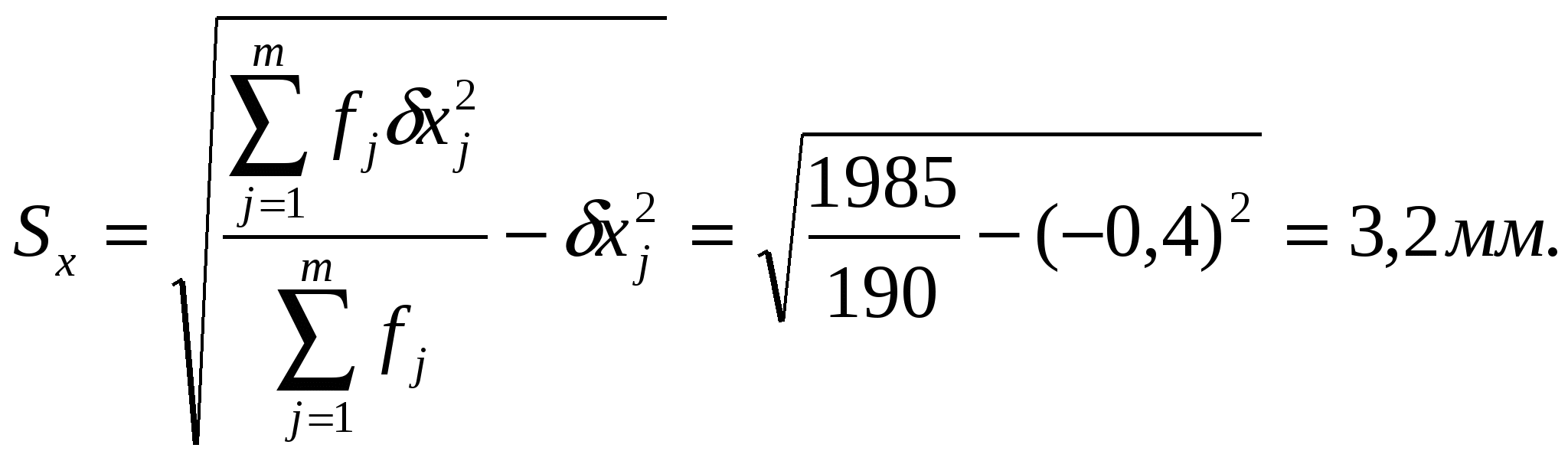 Далее вычисляем значения, соответствующие предельным отклонениям xm + 3Sx = (-0,4)+3*3,2=9,2 мм; xm - 3Sx = (-0,4)-3*3,2=-10 мм. Значения отклонений, вышедшие за пределы, ограниченные вычисленными значениями отсутствуют. Это означает, грубых погрешностей, которых необходимо исключить из объединенной выборки, нет. Поэтому в двух последних графах табл. 3.1 значения сумм 4. Для построения на чертеже гистограммы кривой нормального распределения вычисляем координаты точек кривой - отклонения и соответствующие им частоты f (табл.14). Таблица 4 . Отклонения и соответствующие им частоты f
По полученным координатам и f на гистограмме определим характерные точки, по которым далее построим теоретическую кривую нормального распределения. Очертания гистограммы практически можно считать совпадающими с кривой нормального распределения. Для завершения проверки по гистограмме были суммированы частоты fj по интервалам, расположенным за границами xm tSx при t = 2,0; 2,4; 3,0 и определены соответствующие им суммы частостей. Сравнение сумм частостей в табл. 5 с допустимыми значениями в табл. 5 показывает, что исследуемое распределение можно считать приближающимся к нормальному Таблица 5. Сравнение сумм частостей с допустимыми значениями
5. Для проверки стабильности характеристики Sx из табл. 2 выбираем наибольшее и наименьшее значения Sx max = 3,8 мм и Sx min = 2,63 мм и вычисляем характеристику 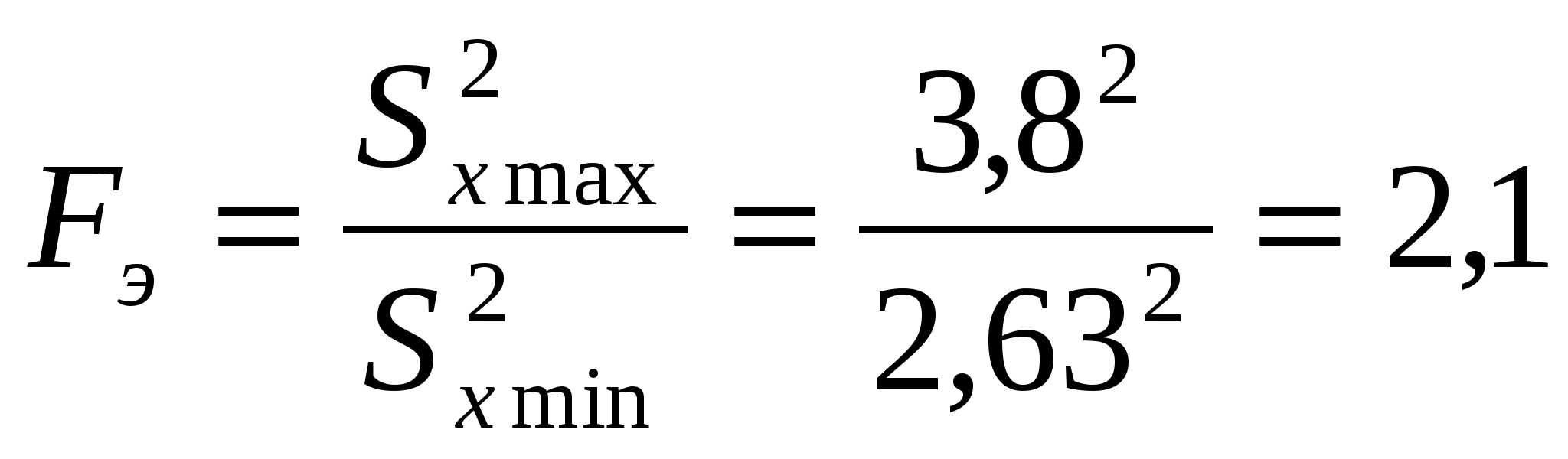 Характеристика Sx в серии выборок не стабильна, так как Fэ = 1,62 > 1,50. Для проверки стабильности характеристики xm выбираем наибольшее и наименьшее значения xm max = 0,105 мм и xm min = -0,74 мм, соответствующие им значения Sx1 = 3,35 мм и Sx2 = 2,63, и вычисляем характеристика Характеристика xm в серии выборок стабильна, так как tэ = 1,2 > 2. Систематическая погрешность, равная найденному выборочному среднему отклонению xm= -0,4 мм, не превышает значение Для определения класса точности по длине панелей определяем значение 2 tSx = 22,13,2=13,44 мм. Значение t = 2,1 примем по табл. 8 для приемочного уровня дефектности AQL = 4,0 %, выбранного по табл. 7. В соответствии с табл.9 ближайшее большее значение допуска для интервала номинальных размеров от 4000 до 8000 мм (L=7000 мм) равно 20 мм, что соответствует 6-му классу точности. По формуле вычисляем значение В соответствии с п. 4 можно сделать вывод, что имеется запас точности, так как 0,33 > 0,14. Вывод:
tэ = 1,2 > 2 стабильна.
Запас точности имеется , так как 0,33 > 0,14.
Стратификация В результате вычислений появился разброс параметров. Чтобы выяснить главную причину его возникновения, следует осуществить расслоение по факторам, порождающим этот разброс. Это поможет уменьшить воздействие этой причины или даже устранить. Проводим стратификацию по оборудованию. Для производства панелей используется 3 станка, для которых получены следующие данные: Таблица 6- Исходные данные по цехам
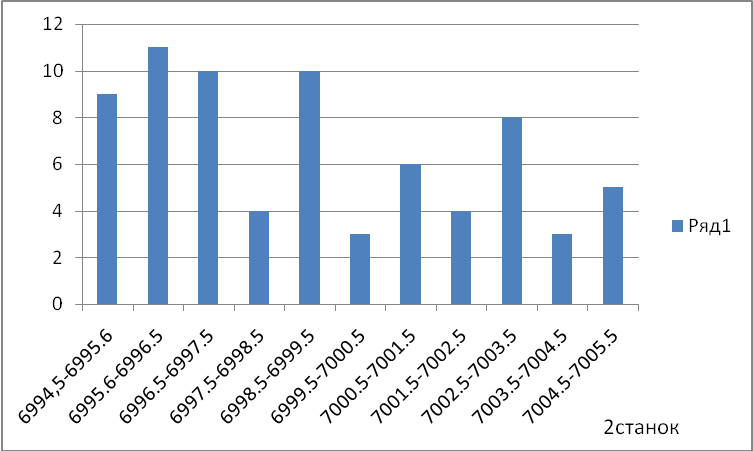 Рисунок 1. Распределение размера плит, изготавливаемого на первом станке. Вывод: Плиты выпускаемые в данном цеху не соответствует норме. Персонал не достаточно как квалифицирован для производства продукции надежного качества. 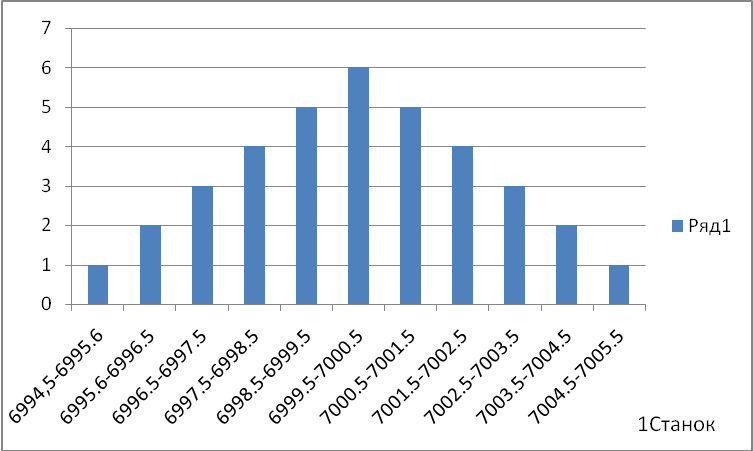 по полученной гистограмме видно что оборудование в цехах настроена правильно и точно. плиты соответствуют нужный длине. работники данного цеха успешно справляется с поставленной работы. 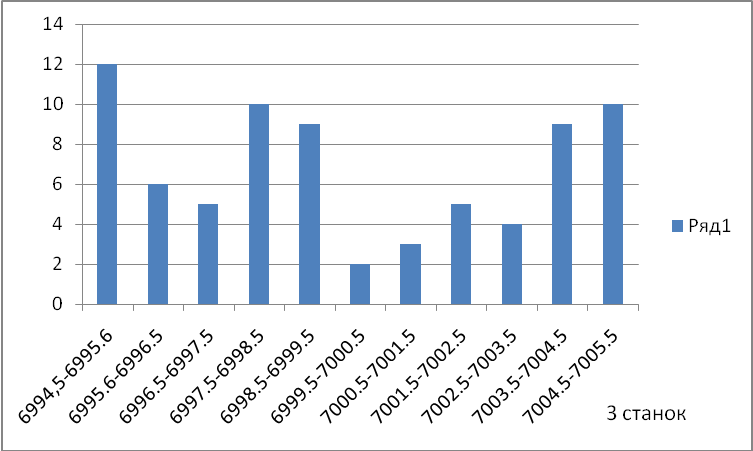 закупка некачественно я и материала привела к выпуску бракованной продукции. Таблица 7- После исправления станков.
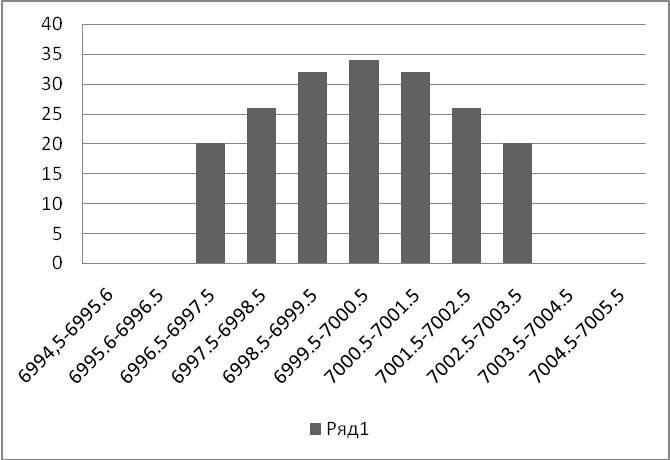 Вывод: после настройки оборудования удалось избавиться от неполадок и плит стали соответствовать нужной длине. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||