лекция. Статистические методы анализа групповых свойств биологических объектов
 Скачать 44.27 Kb. Скачать 44.27 Kb.
|
|
Ф КГМУ 4/3-04/03 ИП №6 от 14 июня 2007 г. Карагандинский государственный медицинский университет Кафедра медицинской биофизики и информатики ЛЕКЦИЯ Тема: «Статистические методы анализа групповых свойств биологических объектов» Дисциплина Biost 3227 Биологическая статистика Специальность 5В130100 - «Общая медицина» Курс ІІІ Время (продолжительность) 1 Караганда 2014 г. Утверждена на заседании кафедры __.__. 20__г. Протокол № ____ Заведующий кафедрой ________________ Койчубеков Б.К. Тема: Статистические методы анализа групповых свойств биологических объектов Цель лекции: Раскрытие сущности и закономерностей массовых явлений и процессов на основании анализа данных, полученных при исследовании отдельных (выборочных) объектов. Дать определения основным статистическим понятиям. План лекции: «Зачем нам это нужно?» Основные понятия и определения биостатистики Виды признаков, используемых в статистическом анализе Характеристики положения Характеристики разброса Нет такого аспекта в сложном процессе создания лекарственных препаратов, в котором не применялись бы методы математической статистики: от процедуры отбора химических соединений для получения заданного спектра биологической активности на первом этапе до прогнозирования продажи уже зарегистрированного препарата. В настоящее время участие специалиста-статистика в планировании и анализе результатов клинических исследований является обычной и широко распространенной практикой. Причем возрастает роль статистика в обсуждении проекта в целом. Применительно к проведению клинических исследований математическая статистика может помочь в формулировании цели, разработке дизайна, выборе методов рандомизации, определении необходимого числа пациентов для получения статистически значимого заключения, непосредственно в проведении анализа полученных результатов, формировании заключения. Применение статистических методов не является формальной процедурой, это — творческая деятельность. И, как любая творческая деятельность, планирование исследований и интерпретация полученных результатов требуют глубоких знаний в области математики. Велика и ответственность — часто именно статистическое оценивание результатов клинических исследований определяет решение в пользу данного метода лечения. На практике статистический анализ или формально выполняют сами медики, или уже после сбора данных их анализ поручается математикам, не имеющим отношения к медицинским приложениям. Кроме того, нередко недостаточное внимание уделяется планированию исследований, в результате уже после окончания этапа сбора информации при попытке применить статистические тесты может оказаться, что собранных данных не хватает для формирования статистически значимого вывода о преимуществах одного сравниваемого метола лечения над другим. И тут даже самые сложные математические методы анализа полученных результатов не спасут ситуацию, если они были получены в ходе неграмотно спланированного исследования. Типы статистических данных Статистические данные представляют собой наблюдаемые или измеряемые значения одного или нескольких признаков обследуемой совокупности объектов. Различают количественные и качественные признаки. Значения количественных признаков могут быть непрерывными (вес, суточная производительность, годовой объем производства) или дискретными (количество детей, год выпуска продукции, количество холодильников, проданных в течение дня). Примерами качественных признаков являются, например, пол, семейное положение, цвет кожи, качество товара. В свою очередь качественные признаки в зависимости от вида данных делятся на номинальные (классификационные) и ординальные (порядковые). Говорят также, что соответствующие качественные признаки измеряются в номинальной или порядковой шкале. Разница между этими шкалами состоит в следующем. Признак, измеряемый в номинальной шкале, принимает одно значение из конечного числа заведомо установленных градаций. Примерами признаков, измеряемых в номинальной шкале, являются пол (мужской, женский), цвет, марка автомобиля, тип строительного материала, классификация животных и т. п. Статистические данные, измеряемые в номинальных шкалах, представляются в виде таблиц, в которых приводятся частоты по-явления той или иной градации признака. Часто номинальные данные появляются при обработке социологических опросов. Например, может представлять интерес вопрос о частоте встречаемости того или иного признака при том или ином заболевании. В этом случае результаты представлены в виде прямоугольной таблицы, содержащей т строк (по числу признаков) и п столбцов (по числу заболеваний), в каждой клетке которой записывается частота встречаемости признака при данном заболвании. Таблицы таких данных называются таблицами сопряженности размера т х п. Значения качественных признаков, измеряемых в ординалъной шкале, могут быть упорядочены. Примерами таких признаков являются тестовые баллы и школьные оценки, качество условий жизни (плохое, удовлетворительное, хорошее, очень хорошее), температура (нормальная, повышенная, высокая, очень высокая и т. д.). Для признаков, измеряемых в ординальных шкалах, операции сложения и вычитания не имеют смысла. Так, нельзя сказать, что студент, получивший на экзамене «пять» по статистике знает предмет на одну единицу лучше, чем студент, получивший по этому предмету «четыре», по-скольку для знаний не существует единицы измерения. Однако можно сказать, что первый студент знает статистику лучше, чем второй. Для представления значений ординальных признаков в числовой форме используется следующий способ. Все значения признака записываются в порядке возрастания в виде ряда. Каждому значению поставим в соответствие натуральное число, равное его номеру в ряду. Это число называется рангом. Например, качество условий жизни (плохое, удовлетворительное, хорошее, очень хорошее) будет представлено рангами 1, 2, 3, 4. Для ординальных признаков, представленных в виде рангов, разработаны специальные статистические методы, позволяющие измерять степень близости признаков (например, ранговая корреляция), проверять гипотезы о виде распределения, проводить дисперсионный анализ. Для данных, представленных в номинальной шкале, также не определены операции сложения и вычитания. Эти данные (в отличие от ординальных признаков) не могут быть упорядочены и, следовательно, оцифрованы с помощью рангов. Применяя специальные статистические методы для номинальных признаков, можно проверить гипотезы о независимости признаков и о принаддежности двух или нескольких выборок к одному виду. Множество всех обследуемых объектов называется генеральной совокупностью. Если это множество содержит небольшое число элементов, то возможно полное обследование генеральной совокупности. Однако в большинстве случаев в силу того, что генеральная совокупность имеет очень много элементов либо ее элементы труднодоступны, либо по другим причинам обследуется некотороя часть генеральной совокупности – выборка. В этом случае основные характеристики генеральной совокупности оцениваются (т.е. определяются приближенно) по выборке. Соответствующие статистики называются «выборочное среднее», «выборочная дисперсия» и т. д. Очевидно, что не всякая выборка правильно отражает свойства генеральной совокупности. Например, нельзя судить о заболеваемости кишечными инфекциями, обследуя только районы с высокими социально-экономическими условиями. Выборка должна давать правильное, неискаженное представление о генеральной совокупности, или, как говорят, быть репрезентативной. Если свойства генеральной совокупности заранее неизвестны, то, за неимением лучшего, следует использовать простой случайный выбор. Это означает, что все элементы генеральной совокупности должны иметь равные шансы попасть в выборку. Например, при выяснении мнения всех студентов университета по какому-либо вопросу, выборка, составленная из студентов первого курса, не будет репрезентативной. Процедуру случайного выбора можно организовать, например, так. Запишем фамилии всех студентов на отдельные карточки, которые затем тщательно перетасуем, и из всего множества карточек отберем нужное количество. Ответы выбранных таким способом студентов составят репрезентативную выборку. Если требуется, чтобы в выборке были представлены элементы различных групп, составляющих генеральную совокупность, используется процедура типического отбора. Так, если студенты первого курса составляют 15% всех студентов университета, то и в выборке они должны составлять 15%. В некоторых случаях необхо-димо учитывать не только курс, но и специализацию студентов, если это может повлиять на результаты опроса. Оценка характеристик генеральной совокупности по выборке Представление данных в виде гистограмм и полигонов дает информацию о распределении генеральной совокупности. Соответствующие гипотезы проверяются по статистическим критериям. Однако часто требуется охарактеризовать генеральную совокупность некоторыми количественными показателями, которые определяют положение центра распределения, рассеяние (разброс) и асимметрию, что дает возможность сравнить одну совокупность данных с другой. По выборке можно определить приближенные значения (оценки) этих числовых характеристик, которые называются выборочными характеристиками. Пусть х1, х2, ..., хn ,— выборка объема п из генеральной совокупности. Выборочный начальный момент r-го порядка определяется как соот-ветствующий момент выборочного распределения и вычисляется по формуле 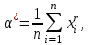 r=1,2,…. r=1,2,….Выборочный начальный момент первого порядка обычно называют средним арифметическим и обозначают х: 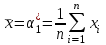 Среднее арифметическое выборки является в определенном смысле «хорошей» оценкой математического ожидания генеральной совокупности для симметричных распределений. Выборочный центральный момент r-го порядка определяется по формуле 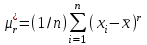 Оценка характеристик положения Наиболее распространенными оценками характеристик положения яв-ляются среднее арифметинеское выборки (выборочнное среднее), выборочная медиана и выборочная мода. В дальнейшем будем опускать термин «выбо-рочная», имея, однако, в виду, что любая оценка, вычисляемая по выборке является всего лишь приближенным значением соответствующей характе-ристики генеральной совокупности. Для выборки объема п: х,, х2, ..., х„ среднее арифметическое равно 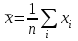 Если выборка представлена в виде статистического ряда, где 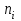 есть частота элемента хi, среднее арифметическое вычисляется по формуле есть частота элемента хi, среднее арифметическое вычисляется по формуле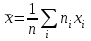 Модой d называется элемент выборки, имеющий наибольшую частоту. Пусть 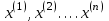 вариационный ряд выборки. Медианой называется число h, которое делит вариационный ряд на две части, содержащие равное число элементов. вариационный ряд выборки. Медианой называется число h, которое делит вариационный ряд на две части, содержащие равное число элементов.Дисперсия определяется по формуле 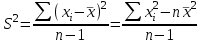 Среднее квадратическое отклонение Sопределяется как арифметический квадратный корень из дисперсии S=√ S2. В качестве меры относительного разброса данных исполъзуют коэффи-циент вариации 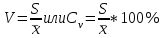 Величину отклонения выборочного показателя (статистики) от его генерального параметра называют статистической ошибкой. Для измерения этой ошибки некоторой статистики квадратичная (стандартная) ошибка статистики (нельзя путать со средним квадратичным отклонением изучаемой случайной переменной). Так, стандартная ошибка среднего арифметического может быть найдена по формуле: 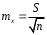 Литература
Контрольные вопросы: Основные задачи биостатистики Классификация признаков Числовые характеристики случайных величи | ||||||||||||||||||||||||||||||||||||||||||
