Статистика. 3167413 Статистика. Статистические величины

• Название: Статистические величины
• Анкор: Статистика
• Дата: 15.12.2021
• Размер: 46.16 Kb.
• Имя файла: 3167413 Статистика.docx
• Тип: Решение; #304971

Статистические величины
Для изучения производительности труда рабочих завода было проведено десяти процентное выборочное обследование по методу случайного бесповторного отбора, в результате которого получены следующие данные о дневной выработке изделий рабочими:

Дневная выработка рабочих.

Таблица 3.2.

Количество изделий за смену, шт.	Число рабочих
18	5
20	10
22	3
24	45
26	15
28	4
30	1

На основании этих данных вычислите:

1. 
   размах вариаций;
   
2. 
   среднее арифметическое значение выработки на одного рабочего;
   
3. 
   среднее линейное отклонение;
   
4. 
   дисперсию;
   
5. 
   среднее квадратичное отклонение;
   
6. 
   коэффициент вариации;
   
7. 
   моду и медиану;
   
8. 
   коэффициент асимметрии. Определите, какая асимметрия наблюдается в данном распределении.
   

Решение

1. Размах вариации представляет собой разницу между максимальным и минимальным значениями ряда и определяется по формуле: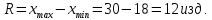



2.Средне арифметическое значение выработки рассчитаем так: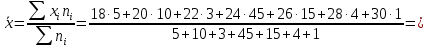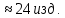





3. Среднее линейное отклонение: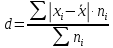



Подставим данные: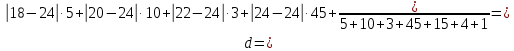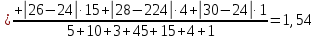





4. Дисперсия: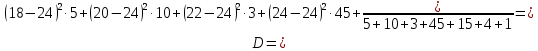







5. Среднее квадратическое отклонение представляет собой квадратный корень из дисперсии: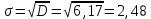



6. Коэффициент вариации: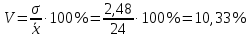



Из полученных результатов можно сделать выводы:

Разница между максимальным и минимальным значениями ряда составляет 12 изделий. Среднее число изделий, производимых рабочим, составляет 24 шт. В среднем каждое значение ряда отличается от среднего значения на 1,54. Общее отклонение всех значений от среднего составляет 6,17. Так как полученный коэффициент вариации меньше 33%, совокупность можно считать однородной.

7. Мода представляет собой наиболее часто встречающееся значение ряда. В данном случае наибольшей частотой обладает выработка 24 шт. за смену. Это значение и будет модой заданного ряда.

Медиана делит выбранную совокупность пополам. Накопленная частота превышает 50% выборки при значении выработки 24 ед. Таким образом, данное значение является медианой ряда. Половина значений меньше данного показателя, вторая половина – больше.

8. Определим коэффициент асимметрии по формуле: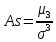



Центральный момент третьего порядка рассчитаем0020следующим образом: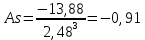







Отрицательный знак полученного значения свидетельствует о наличии левосторонней асимметрии в данном ряду распределения.

Изучение динамики общественных явлений

Производство электроэнергии электростанциями региона "Н" характеризуется следующими данными:

Выпуск электроэнергии в регионе "Н"

Таблица 6.1.

Год	Производство электроэнергии, млрд. квт. ч
1994	3
1995	27,6
1996	26,1
1997	27,4
1998	26,8
1999	27,1
2000	28,6
2001	30,5
2002	32,2

Для анализа ряда динамики определите:

1. 
   показатели, характеризующие динамику производства энергии: абсолютный прирост, ускорение, темпы роста и прироста. Результаты расчетов изложите в табличной форме (табл. 6.2.).
   
2. 
   средний уровень ряда динамики, средний абсолютный прирост, средний темп роста, средний темп прироста.
   

Для определения основной тенденции ряда произведите выравнивание ряда динамики с помощью метода скользящей средней с тремя и пятью членами.

Сравните первоначальный и выровненный ряды с помощью линейной диаграммы.

По результатам задачи сделайте выводы.


Показатели динамики производства электроэнергии региона "Н"

Таблица 6.2.

Производство Электроэнергии млрд. квт. ч	Абсолютный Прирост, Млрд. квт. ч		Ускоре- ние, млрд. квт. ч	Темпы роста, %			Темпы прироста, %
	Цепной способ	Базисный способ		Цепной способ	Базисный способ	Цепной способ	Базисный способ	Значение 1% прироста
3	х	х	х		х	х	х	х	х
27,6	24,6	24,6	9,20		920,00	920	820	820	0,03
26,1	-1,5	23,1	0,95		94,57	870	-5,43	770	0,276
27,4	1,3	24,4	1,05		104,98	913,33	4,98	813,33	0,261
26,8	-0,6	23,8	0,98		97,81	893,33	-2,19	793,33	0,274
27,1	0,3	24,1	1,01		101,12	903,33	1,12	803,33	0,268
28,6	1,5	25,6	1,06		105,54	953,33	5,54	853,33	0,271
30,5	1,9	27,5	1,07		106,64	1016,67	6,64	916,67	0,286
32,2	1,7	29,2	1,06		105,57	1073,33	5,57	973,33	0,305

Рассчитаем средние показатели динамического ряда:

Среднее значения ряда: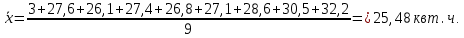



Средний абсолютный прирост:



Среднегодовой темп роста: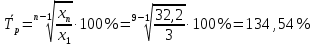



Среднегодовой темп прироста: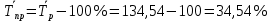



Среднее производство электроэнергии в год составляет 25,48 квт. ч. В среднем с каждым годом производство увеличивалось на 3,65 квт. ч., что в процентном отношении составляет 34,54%.

Упражнение 6.2. Выровняйте представленный в таблице 6.1. динамический ряд методом скользящей средней по три и пять членов.

Таблица 6.3.

Год	Уровень показателя	Сумма трех членов	Скользящая средняя	Сумма пяти членов	Скользящая средняя
1994	3	х	х	х	х
1995	27,6	56,7	18,9	х	х
1996	26,1	81,1	27,0	110,9	22,18
1997	27,4	80,3	26,8	135	27
1998	26,8	81,3	27,1	136	27,2
1999	27,1	82,5	27,5	140,4	28,08
2000	28,6	86,2	28,7	145,2	29,04
2001	30,5	91,3	30,4	х	х
2002	32,2	х	х	х	х

Изобразим полученные данные графически.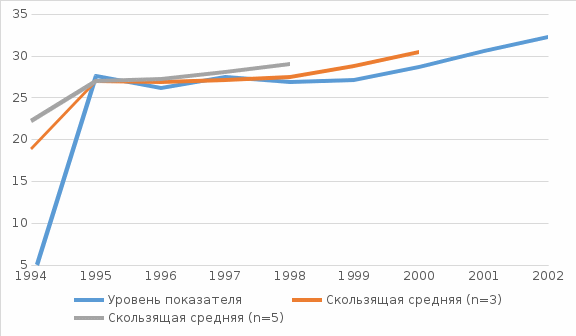



Рис. 1 – Фактические и выровненные данные

Как видно по графику, более точными (близкими к исходным) являются данные, полученные выравниванием 3-х членной скользящей средней.
Индексы

Упражнение 7.1. Используя данные таблицы 7.1., рассчитайте индивидуальные и агрегатные индексы объема, цены и себестоимости.

Таблица характеристик продуктов.

Таблица 7.1.

Продукты	Базисный период			Отчетный период
	Объем, кг q0	Цена, руб. p0	Себестои-мость,руб. z0	Объем, кг q1	Цена, руб. p1	Себестои-мость,руб.z1
А	5000	6	5	4000	8	5
Б	2000	10	8	3500	9	7
В	3000	15	12	2500	16	14

Решение

1. Проведем расчет индивидуальных индексов объема, цены и себестоимости продуктов: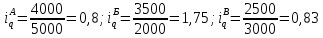







2. Агрегатные индексы:

- индексы физического объема (по цене):



- индексы физического объема (по себестоимости):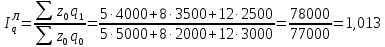



- индекс цен: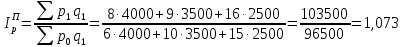



- индекс себестоимости:



Общий индекс товарооборота:



Общий индекс себестоимости продукции: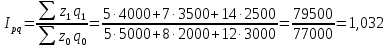



Таким образом, общее изменение объема товарооборота составило 9%. За счет изменения физического объема он увеличился на 1,6%, за счет изменения цен – на 7,3%.

Рассмотрим изменение себестоимости: в отчетном периоде она увеличилась на 3,2%. Изменение физического объемы продукции вызвало снижение себестоимости на 1,3%, а изменение цен – рост на 1,9%.
Список литературы:

1. 
   Балдин, К.В. Общая теория статистики: Учебное пособие / К.В. Балдин, А.В. Рукосуев. - М.: ИТК Дашков и К, 2015. - 312 c.
   
2. 
   Долгова, В.Н. Теория статистики: Учебник и практикум для академического бакалавриата / В.Н. Долгова, Т.Ю. Медведева. - Люберцы: Юрайт, 2016. - 245 c.
   
3. 
   Малых, Н.И. Статистика. т.1 теория статистики: Учебник и практикум для академического бакалавриата / Н.И. Малых. - Люберцы: Юрайт, 2016. - 275 c.