Статистический анализ денежных доходов населения ЦФО. Статистический анализ денежных доходов населения цфо

• Название: Статистический анализ денежных доходов населения цфо
• Анкор: Статистический анализ денежных доходов населения ЦФО
• Дата: 31.08.2022
• Размер: 1.59 Mb.
• Имя файла: Статистический анализ денежных доходов населения ЦФО.docx
• Тип: Курсовая; #657465
• страница: 6 из 10

Корреляционно-регрессионный анализ связи доходов населения ЦФО и ВВП

Корреляционно-регрессионный анализ включает в себя измерение тесноты связи, направление связи и установление аналитического проявление формы связи (уравнения регрессии). Функциональные связи изучаются статистикой связи на основе индексного и балансового методов, корреляционные связи – методов графического изображения, приведения (сравнения) параллельных рядов, аналитических группировок, корреляционно-регрессионного анализа.

На основе данных приложений C и F выясним степень зависимости между доходами населения ЦФО (X) и ВВП в таблице 10.

Таблица 10

Данные для анализа

показатели	2013	2014	2015	2016	2017
ВВП, млрд. руб.	73133,9	79199,7	83387,2	86010,2	92089,3
Центральный федеральный округ	33 466,6	34 970	38 767	39 371	40865

Таблица 11

Затем строим точечный график, добавляем линию тренда (рисунок 5).

Годы	Х	У			x*y
2013	33 466,60	73133,9	1120013316	5348567329,21	2447542977,74	73908,13
2014	34 970	79199,7	1222900900	6272592480,09	2769613509,00	77218,98
2015	38 767	83387,2	1502880289	6953425123,84	3232671582,40	85580,91
2016	39 371	86010,2	1550075641	7397754504,04	3386307584,20	86911,06
2017	40865	92089,3	1669948225	8480439174,49	3763229244,50	90201,22
Итого	187439,60	413820,30	7065818370,56	34452778611,67	15599364897,84	413820,30

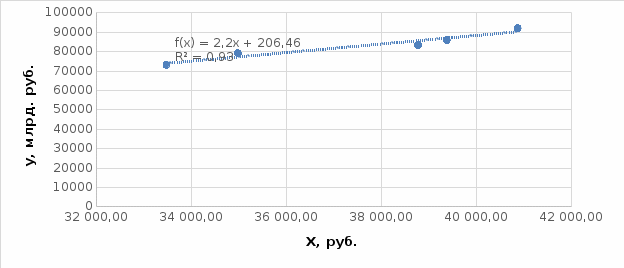Рис. 5. Корреляционно-регрессионный анализ
Определим тесноту корреляционной связи. Для этого необходимо рассчитать линейный коэффициент корреляции:

Линейный коэффициент корреляции: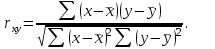



rху=0,96.

Так как 0 ≤ 0,96 ≤ 1, полученное значение линейного коэффициента корреляции говорит о наличии прямой сильной связи между изучаемыми явлениями.

Значимость коэффициентов в простой линейной регрессии (n 30) осуществляется с помощью t-критерия Стьюдента по следующим зависимостям: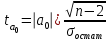

= 0,2 =5,4

где среднее квадратическое отклонение результативного признака у от выровненных значений у:

=1655,9

среднее квадратическое отклонение факторного признака x от общей средней :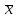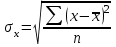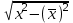

= =2353,4

Полученные значения 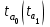сравнивают с критическими по таблицам Стьюдента с учетом принятого уровня значимости и числом степени свободы (n-2), т.е. 3. Обычно =0,05. При нём t_{теор(табл)} = 3,1825.

Если , то это означает, что только параметр t_a1 значим.

Для проверки правильности подбора связи сравним линейный коэффициент корреляции, теоретическое корреляционное соотношение и индекс корреляционной связи.

Теоретическое корреляционное соотношение:

Ƞ=0,96

Индекс корреляционной связи:

R=0,96

Таким образом, , следовательно, связь подобрана верно.

Найдём процент зависимости х и у с помощью коэффициента детерминации:

D=93,2%

Значит, ВВП на 93,2% зависит от доходов населения ЦФО.

В случае линейного уравнения регрессии применяется t – критерий Стьюдента, с помощью которого вычисляется значимость коэффициента корреляции: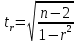

=6,44

При уровне значимости =0,05 и числе степеней свободы 3 табличное значение t-критерия равно 3,1825. Т. к. фактическое значение t-критерия меньше табличного (критического), то коэффициент корреляции значим.

В ходе анализа получено, что коэффициент корреляции значим. Это показывает, что связь между изучаемыми явлениями подобрана верно.