Статистический анализ денежных доходов населения ЦФО. Статистический анализ денежных доходов населения цфо

• Название: Статистический анализ денежных доходов населения цфо
• Анкор: Статистический анализ денежных доходов населения ЦФО
• Дата: 31.08.2022
• Размер: 1.59 Mb.
• Имя файла: Статистический анализ денежных доходов населения ЦФО.docx
• Тип: Курсовая; #657465
• страница: 7 из 10

Расчет относительных величин доли оплаты труда в составе денежных доходов населения

Относительные величины– это показатель, который представляющий собой частное от деления двух статистических величин и характеризующий

Проведем расчеты некоторых относительных величин.

1) Относительная величина структуры. Она характеризует удельный вес составных частей.

2) Относительная величина координации (ОВК) характеризует соотношение отдельных частей целого.

Таблица 12

Объем и структура денежных доходов населения, млрд. руб.

Показатель	2017	ОВС	ОВК
Денежные доходы – всего	55368	100
в том числе:
доходы от предпринимательской деятельности	4229	7,64	0,17
оплата труда2)	36210	65,40	База
социальные выплаты	10855	19,61	0,3
доходы от собственности	2967	5,36	0,08
другие доходы	1107	2,00	0,03

Структура доходов населения в 2017г. на 65,4% состояла из оплаты труда, 19,61% - из социальных выплат, 7,64% - доходы от предпринимательской деятельности, 5,36% - доходы от собственности, 2% - другие доходы.

На 100 руб., приходящихся от оплаты труда приходится 17 руб., полученных от предпринимательской деятельности, 30 руб. – от социальных выплат, 8 руб. – от доходов от собственности 3 руб. от других доодов.

2. 
   Расчет индивидуальных индексов денежных доходов населения
   

Рассчитаем индексы по данным таблицы 13.

Таблица 13

Индивидуальные индексы

	2016	2017	i
Денежные доходы – всего, млрд. руб.	54117	55368	1,02
в том числе:
доходы от предпринимательской деятельности	4209	4229	1,00
оплата труда	34952	36210	1,04
социальные выплаты	10341	10855	1,05
доходы от собственности	3533	2967	0,84
другие доходы	1082	1107	1,02

Расчет индивидуальных индексов показал, что в 2017г. денежные доходы населения выросли на 2%, в том числе: оплата труда выросла на 4%, социальные выплаты – на 5%, другие доходы – на 2%. Доходы от собственности снизились на 16%.

2. 
   Применение выборочного метода для определения границ реальной среднемесячной начисленной заработной платы работников в ЦФО
   

Выборочное наблюдение– это метод статистических исследований, при котором могут обобщаются показатели совокупности и устанавливаются по отдельно взятой части на основе положений случайного отбора.

Далее определяем среднемесячную заработную плату работников в ЦФО в ноябре 2018г. по выборочным данным из таблицы 14.
Таблица 14

Среднемесячная заработная плата работников в ЦФО в ноябре 2018г.

Субъект	Руб.
Центральный федеральный округ	52642
Белгородская область	31163
Брянская область	27403
Владимирская область	31647
Воронежская область	31286
Ивановская область	26053
Калужская область	38005
Костромская область	27948
Курская область	30125
Липецкая область	30775
Московская область	50135
Орловская область	26834
Рязанская область	31192
Смоленская область	29566
Тамбовская область	26754
Тверская область	30764
Тульская область	33933
Ярославская область	33882
г.Москва	78946

Тогда N= 18, а n = 3. Выбираем области:

Брянская – 27403 руб.

Калужская – 38005 руб.

Орловская – 26834 руб.

Расчеты ведем с вероятностью 0,997 ( ).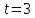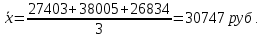


Рассчитаем дисперсию: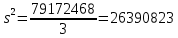



Средняя ошибка выборки будет равна: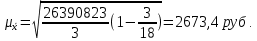



Найдем предельную ошибку выборки для среднего значения: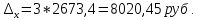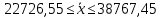