курсовая. Статистический анализ государственного бюджета
 Скачать 0.81 Mb.
|
|
Задача 8. Менеджер компании, занимающейся прокатом автомобилей, хочет оценить среднюю величину пробега одного автомобиля в течение месяца. Из 280 автомобилей, принадлежащих компании, методом случайной бесповторной выборки отобрано 30. По данным этой выборки установлено, что средний пробег автомобиля в течение месяца составляет 1342 км. со стандартным отклонением 227 км. Считая пробег автомобиля случайной величиной, распределённой по нормальному закону, найдите 95%-ный доверительный интервал, оценивающий средний пробег автомобилей всего парка в течение месяца. Решение: (Средний пробег автомобилей всего парка) 95% =0,954; t(0,954) =2(коэффициент доверия)  = 227 кмn= 30 шт. N = 280 шт.  = кмНайдем интервал, оценивающий средний пробег автомобилей всего парка в течение месяца (  ).1342 км  78,3 кмИнтервал:  кмВывод: В 95% средний пробег автомобиля не выйдет за предел диапазона км. Задача 9. Среднемесячный бюджет студентов в колледжах одного из штатов США оценивается по случайной выборке. С вероятностью 0,954 найдите наименьший объём выборки, необходимой для такой оценки, если среднее квадратическое отклонение предлагается равным 100 у.е., а предельная ошибка средней не должна превышать 20 у.е. Решение: t(0,954)=2 =100 у.е  =20 y.e.Найдем наименьший объем выборки:  1000 у.е. Вывод: Наименьший объем выборки с вероятностью 0,954 составляет 1000 у.е. Задача 10. Организация стран-экспортёров нефти предпринимает попытки контроля над ценами на сырую нефть с 1973 г. Цены на сырую нефть резко возрастали с середины 70-х до середины 80-х гг., что повлекло за собой некоторое повышение цен на бензин.
Постройте график и оцените характер взаимосвязи между переменными. Рассчитайте параметры уравнения регрессии, оценивающего зависимость цен на галлон бензина от цен за баррель нефти. Дайте интерпретацию полученных результатов. Решение: Построим поле корреляции и прямую регрессии: 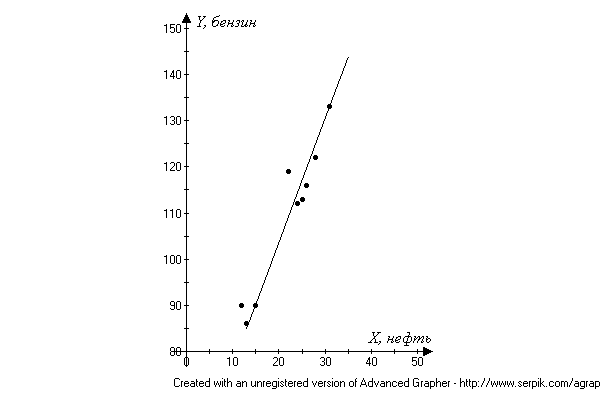 Рис. 1. Поле корреляции и прямая регрессии  - уравнение регрессии 
 долл. цент.  долл. ; .Вывод: Связь между бензином и нефтью функциональная. Таким образом, с увеличение цены нефти на 1 долл. цена бензина за галлон увеличилась на 2 цента. Задача 11. Исследуйте связь между успеваемостью студентов-заочников вуза и работой их по специальности. Результаты характеризуются следующими данными:
Решение:
 – студенты, работающие по специальности; – студенты, работающие не по специальности; – работающие по специальности получили полож. оценки; – работающие по специальности получили неудовл. оценки; – не работающие по специальности получили полож. оценки; – не работающие по специальности получили неуд. оценки.Вывод: Работа по специальности влияет на успеваемость, так как студентов, получивших положительные оценки и работающих по специальности в 5 раз больше, чем студентов, работающих не по специальности и получивших положительную оценку. Задача 12. Имеются следующие данные по предприятию за год: 1.Среднесписочное число работников, всего, чел. 1000 в том числе: с продолжительностью рабочего дня 8,0 часов 950 с продолжительностью рабочего дня 7,0 часов (рабочих горячих цехов) 50 2.Отработано работниками, человеко-дней 214 200 3.Целодневные простои, человеко-дней 40 4.Неявки на работу, человеко-дней 150 760 в том числе: ежегодные отпуска 22 000 праздничные и выходные дни, человеко-дней 113 000 Определить: 1. Календарный фонд рабочего времени 2. Максимально возможный фонд рабочего времени 3. Коэффициент использования календарного фонда времени 4. Коэффициент использования максимально возможного фонда времени 5. Описать полученные результаты. Решение: 1.Найдем календарный фонд рабочего времени: КФРВ=ССЧ  365(366)=1000365=365000 человеко-дней;2.Найдем максимально возможный фонд рабочего времени: МВФРВ=КФРВ – ежегодные отпуска – праздничные и выходные дни = =365000–22000–113000=230000 человеко-дней; 3.Найдем коэффициент использования календарного фонда времени: КИКФВ = число отработанных человеко-дней / КФРВ =  0,58 или 58%Таким образом, 58% затрачено на фактическую работу. 4.Найдем коэффициент использования максимально возможного фонда времени: КИМВФВ= число отработанных человеко-дней / МВФВ =  0,93 или 93%Вывод: КФРВ равен 365000 человеко-дней, МВФРВ равен 230000 человеко-дней, коэффициент использования календарного фонда времени равен 0,58 или 58% и Коэффициент использования максимально возможного фонда времени равен 0,93. Задача 13. Рассчитать индексы сезонности и построить график сезонной волны по следующим данным о производстве яиц за 3 года:
Решение: 1.Рассчитаем индексы сезонности. Найдем сколько в среднем яиц, производилось за 3 года в каждом месяце:  яиц – в январе; яиц – в феврале; яиц – в марте; яиц – в апреле; яиц – в мае; яиц – в июне; яиц – в июле; яиц – в августе; яиц – в сентябре; яиц – в октябре; яиц – в ноябре; яиц – в декабре;Найдем среднее значение у:  яиц.Найдем индексы сезонности:   или 57% – производство снизилось в январе на 43%;  или 82% – производство снизилось в феврале на 18%; или 86% – производство снизилось в марте на 14%; или 106% – производство увеличилось в апреле на 6%; или 137% – производство увеличилось в мае на 37%; или 141% – производство увеличилось в июне на 41%; или 140% – производство увеличилось в июле на 40%; или 123% – производство увеличилось в августе на 23%; или 110% – производство увеличилось в сентябре на 10%; или 83% – производство снизилось в октябре на 17%; или 56% – производство снизилось в ноябре на 44%; или 72% – производство снизилось в декабре на28%.2.Построим график сезонной волны: 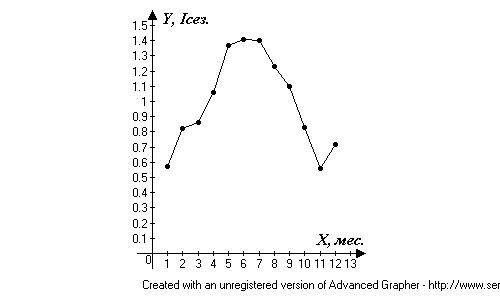 Рис. 2. График сезонной волны Вывод: Пик производства яиц за 3 года наблюдается в июне(6), а спад в ноябре месяце (1). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
