курсовая. Статистический анализ государственного бюджета
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
|
Задача 14. Провести индексный анализ фондоотдачи, фондоёмкости и фондовооружённости по следующим данным:
Решение: Фондоотдача – показывает, сколько продукции в стоимостном выражении выпускается на 1 рубль стоимости основных фондов: где, Q – объём товаров и услуг выпущенных предприятием в данный период; Ф – средняя стоимость основных фондов в данном периоде. Фондоёмкость – характеризует стоимость основных производственных фондов, приходящих на 1 рубль производственных товаров и услуг: Фондовооружённость – характеризует, как работники обеспечены основными фондами: 1.Найдем фондоотдачу: Найдем индекс фондоотдачи: Таким образом, фондоотдача отчетного года уменьшилась по сравнению с базисным годом на 21% или на 1,15 руб. 2.Найдем фондоёмкость: Найдем индекс фондоёмкости: Таким образом, фондоемкость отчетного года увеличилась по сравнению с базисным годом на 22% или на 0,04 руб. 3.Найдем фондовооруженность: Найдем индекс фондовооруженности: Таким образом, фондовооруженность отчетного года уменьшилась по сравнению с базисным годом на 24% или на 18,5 руб. Задача 15. Проанализировать движение основных фондов предприятия (коэффициенты обновления, выбытия, годности) по следующим данным, тыс. руб.:
Решение: 1.Найдем наличие на конец года всех основных фондов предприятия: Наличие на конец года всех основных фондов предприятия = =наличие на конец года – выбыло за год + поступило за год; Найдем наличие на конец года всех фондов предприятия с учетом амортизации: Наличие на конец года с учетом амортизации = наличие на конец года – амортизация.
2)Найдем: Коэффициент обновления = поступило за год/ наличие на конец года Коэффициент выбывания = выбыло за год/ наличие на начало года Коэффициент годности = годность ОС/ наличие на конец года
Вывод: Наибольшие обновления произошли у машин и оборудования. Наибольший коэффициент выбывания наблюдается у транспортных средств. Наибольший коэффициент годности у основных средств – инструмент и инвентарь. Задача 16. Ежегодное изменение физического объёма ВВП характеризуется следующим рядом динамики:
Проанализировать данный ряд с помощью показателей динамики (абсолютных, относительных и средних). Построить график, сделать выводы. Решение: 1.Найдем показатели динамики:
2.Построим график динамики уровня ряда за период 1 – 8 гг. 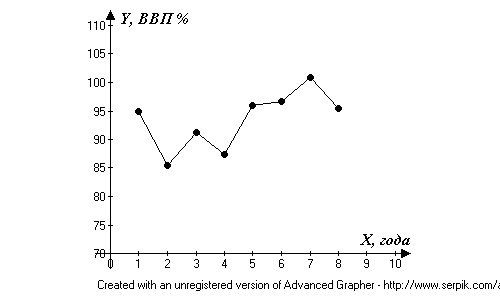 Рис. 3. График динамики уровня ряда Вывод: В среднем ВВП составляет 93,5%, при этом средний темп роста равен 1,а средний темп прироста не наблюдается. Самый низкий показатель ВВП за 2-ой год, самый высокий за 7-ой год. Задача 17. Имеются следующие данные о расходе проката чёрных металлов на предприятии:
Определить индексы удельного (на ед.) и общего расхода проката, экономию материалов. Решение: 1.Определим индексы удельного проката: Таким образом, удельный расход проката уменьшился на 5% или на 380 кг на ед.– для трактора. Таким образом, удельный расход проката уменьшился на 1% или на 20 кг на ед. – для комбайна. 2.Определим индексы общего расхода проката: Таким образом, общий расход проката уменьшился на 5% или на 3620000 – 3810000= –190000 кг на ед.– для трактора. Таким образом, общий расход проката уменьшился на 1% или на 460000 – 464000 = –4000 кг на ед. – для комбайна. Задача 18. Для определения среднего возраста 1200 студентов факультета необходимо провести выборочное обследование методом случайного бесповторного отбора. Предварительно установлено, что среднее квадратическое отклонение возраста студентов равно 10 годам. Сколько студентов надо обследовать, чтобы с вероятностью 0,954 средняя ошибка выборки не превышала 3 года? Решение: t(0,954)=2; N=1200; Вывод: Надо обследовать 43 студента, чтобы с вероятностью 0,954 средняя ошибка выборки не превышала 3 года. Задача 19. По имеющимся данным рассчитать среднее содержание меди в образцах, моду, медиану, сделать вывод о симметричности распределения.
Решение: 1.Найдем показатели дискретного ряда:
Таким образом, среднее содержание меди в образцах составляет 65%. 2.Найдем моду и медиану: 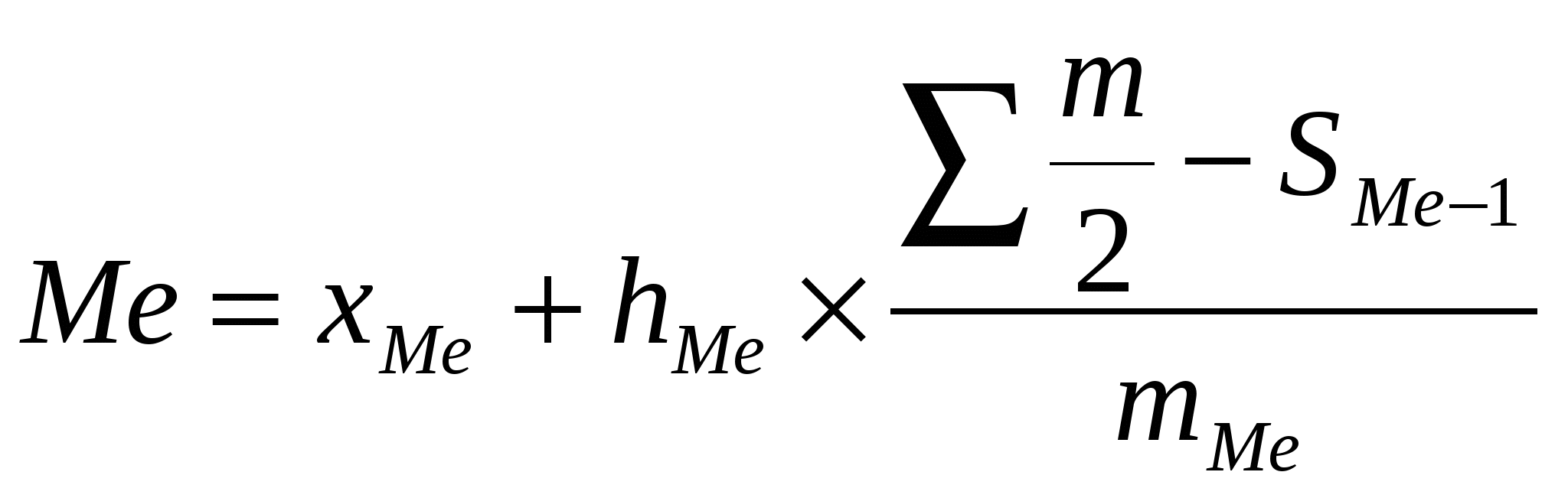 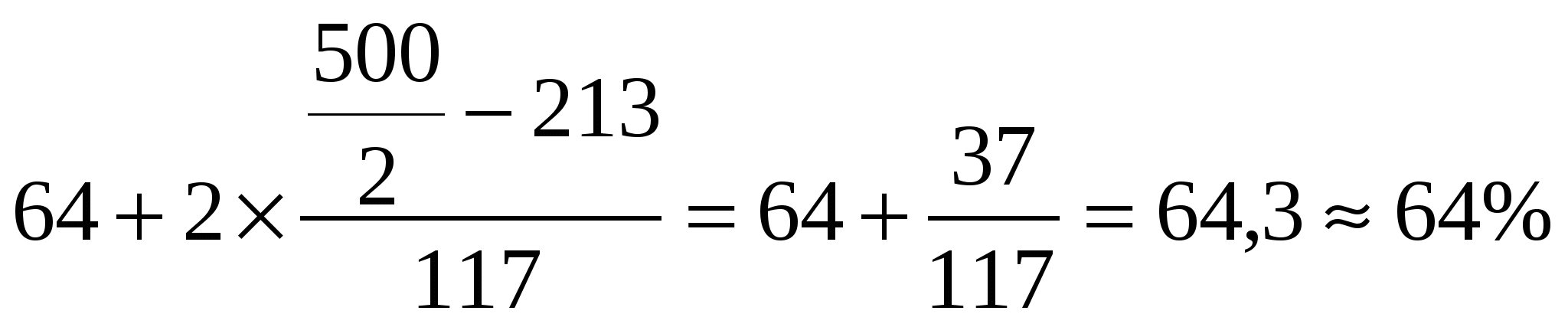 Вывод: Ряд является симметричным, так как мода примерно равна медиане: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
