ЗАОЧНИКИ_ЭКОНОМЕТРИКА_ЛЕКЦИИ. Степанов в. Г. Краткое историческое введение

• Название: Степанов в. Г. Краткое историческое введение
• Анкор: ЗАОЧНИКИ_ЭКОНОМЕТРИКА_ЛЕКЦИИ.doc
• Дата: 25.04.2017
• Размер: 0.78 Mb.
• Имя файла: ЗАОЧНИКИ_ЭКОНОМЕТРИКА_ЛЕКЦИИ.doc
• Тип: Курс лекций; #5473
• страница: 3 из 8

Тогда средняя ошибка аппроксимации равна .

Из практики известно, что значение средней ошибки аппроксимации не должно превышать (12…15)%

На последнем этапе выполним оценку статистической надежности моделирования с помощью F – критерия Фишера. Для этого выполним проверку нулевой гипотезы Н₀ о статистической не значимости полученного уравнения регрессии по условию:

если при заданном уровне значимости a = 0,05 теоретическое (расчетное) значение F – критерия F_т больше его критического значения F_{крит (табличного)}, то нулевая гипотеза отвергается, и полученное уравнение регрессии принимается значимым.

Из рисунка 1.4 следует, что F_т = 0,0058. Критическое значение F – критерия F_крит, определяем с помощью использования статистической функции FРАСПОБР ( ) рисунок 1.5.. Входными параметрами функции является уровень значимости (Вероятность) и число степеней свободы 1 и 2 . Для модели парной регрессии число степеней свободы соответственно равно 1 (одна объясняющая переменная) и n-2 = 6-2= 4.
Рисунок 1.5. Окно статистической функции FРАСПОБР

И
з рисунка 1.5 видно, что критическое значение F – критерия F_крит =7,71.

Так как F_т < F_крит , то нулевая гипотеза не отвергается и полученное регрессионное уравнение статистически незначимо.
Более сложное задание. Построение модели множественной регрессии
В соответствии с вариантом задания, используя статистический материал, необходимо.

1. 
   Построить линейное уравнение множественной регрессии пояснить экономический смысл его параметров.
   
2. 
   Дать сравнительную оценку тесноты связи факторов с результативным признаком с помощью средних (общих) коэффициентов эластичности.
   
3. 
   Оценить статистическую значимость коэффициентов регрессии с помощью t –- критерия и нулевую гипотезу о значимости уравнения с помощью F – критерия.
   
4. 
   Оценить качество уравнения посредством определения средней ошибки аппроксимации
   

Исходные данные для построения модели парной регрессии приведены в таблице 1.3.
Таблица 1.3. Исходные данные

№ п/п	Чистый доход, мл. долл. США, у	Оборот капитала, мл. долл. США, х1	Использованный капитал, мл. долл. США, х2
1	6,6	6,9	83,6
2	2,7	93,6	25,4
3	1,6	10,0	6,4
4	2,4	31,5	12,5
5	3,3	36,7	14,3
6	1,8	13,8	6,5
7	2,4	64,8	22,7
8	1,6	30,4	15,8
9	1,4	12,1	9,3
10	0,9	31,3	18,9

Технология построения уравнения регрессии аналогична алгоритму, изложенному в п.п.1.1. Протокол построения уравнения регрессии показан на рисунке 1.6.
Рисунок 1.6. Протокол решения задачи

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,901759207
R-квадрат	0,813169667
Нормированный R-квадрат	0,759789572
Стандартная ошибка	0,789962026
Наблюдения	10
Дисперсионный анализ
	df	MS	F	Значимость F
Регрессия	2	9,50635999	15,23357468	0,00281881
Остаток	7	0,624040003
Итого	9
	Коэффициенты	t-статистика
Y-пересечение	1,113140304	2,270238114
Переменная X 1	-0,000592199	-0,061275574
Переменная X 2	0,063902851	5,496523193

Из рисунка 1.6 видно, что эмпирические коэффициенты регрессии соответственно равны b₀ = 1,11, b₁ = -0, 0006, b₂ = 0, 064. Тогда уравнение множественной линейной регрессии, связывающая величину чистого дохода у с оборотом капитала х₁ и использованным капиталом х₂ имеет вид имеет вид.
. (1.5)

На следующем этапе, в соответствии с заданием необходимо определить степень связи объясняющих переменных х₁ и х₂ с зависимой переменной у, используя коэффициенты эластичности. Коэффициенты эластичности для модели множественной линейной регрессии определяется в виде:

. (1.6)

Тогда

. (1.7)

Следовательно, при изменении оборота капитала 1% величина чистого дохода копании изменяется на 0,0008%. .

При изменении использованного капитала на 1% величина чистого дохода компании изменяется на 0,56%.

На третьем этапе исследования необходимо оценить статистическую значимость коэффициентов регрессии с помощью t – критерия и нулевую гипотезу о значимости уравнения с помощью F – критерия.

Технология оценки статистической значимости коэффициентов регрессии также основывается на проверке нулевой гипотезы о не значимости коэффициентов регрессии. При этом проверяется выполнение условия:
если t_т > t_крит , то нулевая гипотеза отвергается, и коэффициент регрессии принимается значимым. Из рисунка 3.6 видно, что t_т для первого коэффициента регрессии равен -0,061, а для второго 5,5. Критическое значение t_крит при уровне значимости a = 0,05определяем с использованием статистической функции СТЬЮДРАСПОБР ( ) рисунок. Входными параметрами функции является уровень значимости (Вероятность) и число степеней свободы. Для рассматриваемого примера число степеней свободы соответственно равно n-3 (так как, для двухфакторной модели множественной регрессии оценивается три параметра b₀ ,b₁, b₂ ) Тогда число степеней свободы равно10-3=7.
Рисунок 1.7. Окно статистической функции СТЬЮДРАСПОБР

И
з рисунка 1.7 видно, что критическое значение t_крит =2,36.

Так как t_т < t_крит , для первого коэффициента регрессии (0,061< 2,36) то нулевая гипотеза не отвергается и объясняющая переменная х₁ является статистически незначимой и ее можно исключить из уравнения регрессии. И наоборот, для второго коэффициента регрессии t_т > t_крит (5,5 >2,36), и объясняющая переменная х₂ является статистически значимой.

Проверка значимости уравнения множественной регрессии в целом с использованием F – критерия аналогична проверке уравнения парной регрессии.

Из рисунка 3.6 следует, что F_т = 15,23. Критическое значение F – критерия F_крит, определяем с помощью использования статистической функции FРАСПОБР ( ). Для модели множественной регрессии с двумя переменными число степеней свободы соответственно равно 2 (две объясняющие переменные х₁ и х₂) и n-k –1(где k=2 – число объясняющих переменных). И второе число степеней свободы равно10-3=7. Критическое значение F_крит = 4,74. Следовательно:

F_т > F_крит, (15,23 > 4,74), и уравнение регрессии в целом является значимым.

На последнем этапе исследования необходимо оценить качество уравнения посредством определения средней ошибки аппроксимации по зависимости (1.4). С этой целью представим таблицу 1.3 в виде вспомогательной таблицы 1.4. Тогда средняя ошибка аппроксимации составит:

. (1.8)

Таким образом:

1. Сформирована эконометрическая модель в виде линейного уравнения парной регрессии, связывающая величину ежемесячной пенсии у с величиной прожиточного минимума х: .

2. На основании анализа численного значения коэффициента корреляции = 0,038 установлено отсутствие статистической связи между величиной прожиточного минимума х и величиной ежемесячной пенсии у. Показано, что доля всех неучтенных в полученной эконометрической модели объясняющих переменных приблизительно составляет 99,8%.
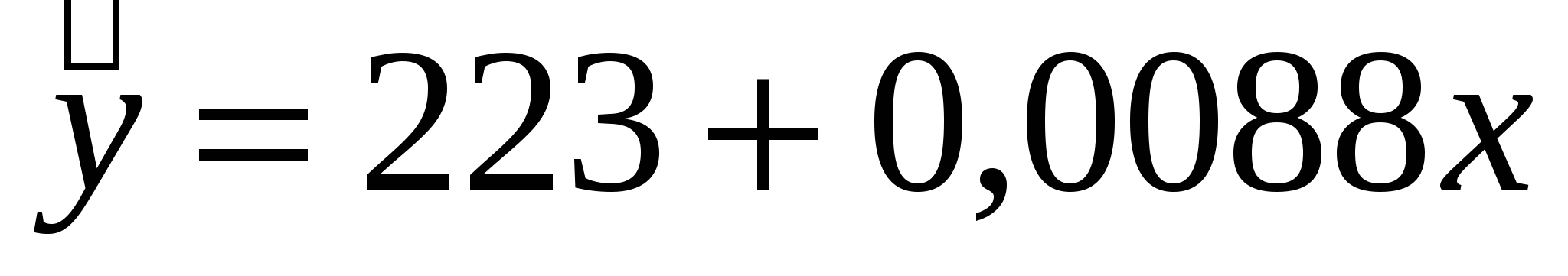3. Путем расчета коэффициента эластичности показано, что при изменении прожиточного минимума на 1% величина ежемесячной пенсии изменяется несущественно, всего на 0,000758%.