ЗАОЧНИКИ_ЭКОНОМЕТРИКА_ЛЕКЦИИ. Степанов в. Г. Краткое историческое введение
 Скачать 0.78 Mb.
|
|
ЛЕКЦИЯ 2. ОБОСНОВАНИЕ КРИТЕРИЕВ ПРОВЕРКИ СТАТИСТИЧЕСКИХ ГИПОТЕЗ (ЗНАЧИМОСТИ РЕГРЕССИИ) Вернемся теперь к обоснованию критериев проверки значимости найденных по методу наименьших квадратов (МНК) параметров модели регрессии ( и вообще методов проверки статистических гипотез). После того, как найдено уравнение линейной регрессии, производится оценка значимости как уравнения в целом, так и отдельных его параметров. Оценка значимости уравнения регрессии в целом может выполняться с помощью различных критериев. Достаточно распространенным и эффективным является применение F-критерия Фишера. При этом выдвигается нулевая гипотеза. Но, что коэффициент регрессии равен нулю, т.е. b=0, и, следовательно, фактор х не оказывает влияния на результат у. Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной у от среднего значения у на две части - «объясненную» и «необъясненную»:  (2.1)Общая сумма квадратов отклонений индивидуальных значений результативного признака у от среднего значения у вызвана влиянием множества факторов. Условно разделим всю совокупность причин на две группы: изучаемый фактор х и прочие факторы. Если фактор не оказывает влияния на результат, то линия регрессии на графике параллельна оси ОХ и у=у. Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадет с остаточной. Если же прочие факторы не влияют на результат, то у связан с х функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов. Поскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет место их разброс как обусловленный влиянием фактора х, т.е. регрессией у по х, так и вызванный действием прочих причин (необъясненная вариация). Пригодность линии регрессии для прогноза зависит от того, какая часть общей вариации признака у приходится на объясненную вариацию. Очевидно, что если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор х оказывает существенное воздействие на результату. Это равносильно тому, что коэффициент детерминации  будет приближаться к единице. Любая сумма квадратов отклонений связана с числом степеней свободы, т.е. числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности лис числом определяемых по ней констант. Применительно к исследуемой проблеме число степеней свободы должно показать, сколько независимых отклонений из п возможных [(у1-у),(у2-у),..(уп-у)] требуется для образования данной суммы квадратов. Так, для общей суммы квадратов ∑(у-у)2требуется (п-1) независимых отклонений, т.к. по совокупности из п единиц после расчета среднего уровня свободно варьируют лишь (п-1) число отклонений. При расчете объясненной или факторной суммы квадратов ∑(у-у)2используются теоретические (расчетные ) значения результативного признака у*, найденные по линии регрессии: у(х)=а+bх.Вернемся теперь к разложению общей суммы квадратов отклонений результативного фактора от среднего этой величины. Эта сумма содержит две уже определенные выше части: сумму квадратов отклонений, объясненную регрессией и другую сумму, которая называется остаточная сумма квадратов отклонений. С таким разложением связан анализ дисперсии, который прямо отвечает на принципиальный вопрос: как оценить значимость уравнения регрессии в целом и его отдельных параметров? Оно же в значительной мере и определяет смысл этого вопроса. Для оценки значимости уравнения регрессии в целом используется критерий Фишера (F-критерий). Согласно подходу, предложенному Фишером, выдвигается нулевая гипотеза  : коэффициент регрессии равен нулю, т.е. величина b=0. Это означает, что фактор х не оказывает влияния на результат у.Вспомним, что практически всегда полученные в результате статистического исследования точки не ложатся точно на линию регрессии. Они рассеяны, будучи удалены более или менее сильно от линии регрессии. Такое рассеяние обусловлено влиянием прочих, отличных от объясняющего фактора х , факторов, не учитываемых в уравнении регрессии. При расчете объясненной, или факторной суммы квадратов отклонений используются теоретические значения результативного признака, найденные по линии регрессии. Для заданного набора значений переменных у и х расчетное значение среднего величины у является в линейной регрессии функцией только одного параметра – коэффициента регрессии. В соответствии с этим факторная сумма квадратов отклонений имеет число степеней свободы, равное 1. А число степеней свободы остаточной суммы квадратов отклонений при линейной регрессии равно n-2. Следовательно разделив каждую сумму квадратов отклонений в исходном разложении на свое число степеней свободы получаем средний квадрат отклонений (дисперсию на одну степень свободы). Далее разделив факторную дисперсию на одну степень свободы на остаточную дисперсию на одну степень свободы получаем критерий для проверки нулевой гипотезы так называемое F-отношение, или одноименный критерий. Именно, при справедливости нулевой гипотезы факторная и остаточная дисперсии оказываются просто равны друг другу. Для отклонения нулевой гипотезы, т.е. принятия противоположной гипотезы, которая выражает факт значимости (наличия) исследуемой зависимости, а не просто случайного совпадения факторов, имитирующего зависимость, которая фактически не существует необходимо использовать таблицы критических значений указанного отношения. По таблицам выясняют критическую (пороговую) величину критерия Фишера. Она называется также теоретической. Затем проверяют сравнивая ее с вычисленным по данным наблюдений соответствующим эмпирическим (фактическим) значением критерия, превосходит ли фактическая величина отношения критическую величину из таблиц. Более подробно это делается так. Выбирают данный уровень вероятности наличия нулевой гипотезы и находят по таблицам критическое значение F-критерия, при котором еще может происходить случайное расхождение дисперсий на 1 степень свободы, т.е. максимальное такое значение. Затем вычисленное значение отношения F-признается достоверным (т.е. выражающим различие фактической и остаточной дисперсий), если это отношение больше табличного. Тогда нулевая гипотеза отклоняется (неверно, что отсутствуют признаки связи) и напротив приходим к заключению, что связь имеется и является существенной (носит неслучайный, значимый характер). В случае, если величина отношения оказывается меньше табличного, то вероятность нулевой гипотезы оказывается выше заданного уровня (который выбирался изначально) и нулевая гипотеза не может быть отклонена без заметной опасности получить неверный вывод о наличии связи. Соответственно уравнение регрессии считается при этом незначимым. Сама величина F-критерия связана с коэффициентом детерминации. Помимо оценки значимости уравнения регрессии в целом оценивают также значимость отдельных параметров уравнения регрессии. При этом определяют стандартную ошибку коэффициента регрессии с помощью эмпирического фактического среднеквадратичного отклонения и эмпирической дисперсии на одну степень свободы. После этого используют распределение Стьюдента для проверки существенности коэффициента регрессии для расчета его доверительных интервалов. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента выполняется посредством сопоставления значений этих величин и величины стандартной ошибки. Величина ошибки параметров линейной регрессии и коэффициента корреляции определяется по следующим формулам:  (2.2)и  , (2.3)где S – среднеквадратичное остаточное выборочное отклонение, rxy – коэффициент корреляции. Соответственно величина стандартной ошибки, предсказываемой по линии регрессии, дается формулой: 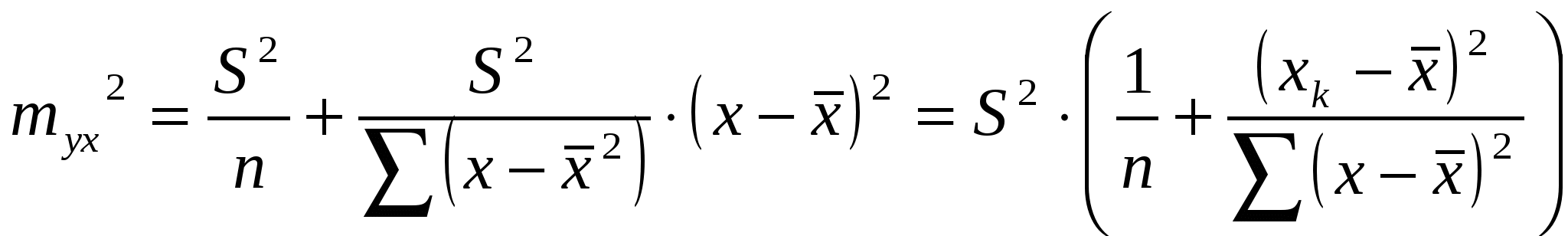 (2.4)Соответствующие отношения значений величин коэффициентов регрессии и корреляции к их стандартной ошибке образуют так называемую t-статистику, а сравнение соответствующего табличного (критического) значения ее и ее фактического значения позволяет принять или отвергнуть нулевую гипотезу. Нo далее для расчета доверительного интервала находится предельная ошибка для каждого показателя как произведение табличного значения статистики t на среднюю случайную ошибку соответствующего показателя. По сути, чуть иначе мы уже фактически записали ее только что выше. Затем получают границы доверительных интервалов: нижнюю границу вычитанием из соответствующих коэффициентов (фактически средних) соответствующей предельной ошибки, а верхнюю границу – сложением (прибавлением). В линейной регрессии ∑(yx-y)2=b2 ∑(x-x)2. В этом нетрудно убедиться , обратившись к формуле линейного коэффициента корреляции: rху=bitσх/σу r2xy=b2itσ2x/σ2y, где σ2y- общая дисперсия признака у; b2itσ2x- дисперсия признака у обусловленная фактором х. Соответственно сумма квадратов отклонений , обусловленных линейной регрессией, составит: σ∑(yx-y)2=b2∑(x-x)2. Поскольку при заданном объеме наблюдений по х и у факторная сумма квадратов при линейной регрессии зависит только от одной константы коэффициента регрессии b, то данная сумма квадратов имеет одну степень свободы. Рассмотрим содержательную сторону расчетного значения признака у т.е. ух. Величина ух определяется по уравнению линейной регрессии: ух=а+bх. Параметр а можно определить, как а=у-bх. Подставив выражение параметра а в линейную модель, получим: yx=y-bx+bx=y-b(x-x). При заданном наборе переменных у и х расчетное значение ух является в линейной регрессии функцией только одного параметра - коэффициента регрессии. Соответственно и факторная сумма квадратов отклонений имеет число степеней свободы, равное 1. Существует равенство между числом степеней свободы общей, факторной и остаточной суммами квадратов. Число степеней свободы остаточной суммы квадратов при линейной регрессии составляет (п-2).Число степеней свободы для общей суммы квадратов определяется числом единиц, и поскольку мы используем среднюю вычисленную по данным выборки, то теряем одну степень свободы, т.е. (п-1). Итак, имеем два равенства: для сумм и для числа степеней свободы. А это в свою очередь возвращает нас опять к сопоставимым дисперсиям на одну степень свободы, отношение которых и дает критерий Фишера. Аналогично отношению Фишера отношение величин параметров уравнения или корреляционного коэффициента к величине стандартной ошибки соответствующих коэффициентов образует критерий Стьюдента для проверки значимости этих величин. Далее также используются таблицы распределения Стьюдента и сравнение расчетных (фактических) значений с критическими (табличными). Однако, более того, проверка гипотез о значимости коэффициентов регрессии и корреляции в нашем простейшем случае равносильна проверке гипотезы о существенности линейного уравнения регрессии по Фишеру (квадрат т-критерия Стьюдента равен критерию Фишера). Все описанное выше справедливо пока величина коэффициента корреляции не близка к 1. Если величина коэффициента корреляции близка к 1, то распределение его оценок отличается от нормального распределения или от распределения Стьюдента. В этом случае согласно Фишеру для оценки существенности коэффициента корреляции вводят новую переменную z для которой: Z= (½)ln{(1+r)/(1-r)} (2.5) Эта новая переменная z изменяется в неограниченных пределах от – бесконечности до + бесконечности и распределена уже весьма близко к нормальному закону. Для этой величины имеются рассчитанные таблицы. И поэтому удобно использовать ее для проверки значимости коэффициента корреляции в указанном случае. ЛЕКЦИЯ 3. НЕЛИНЕЙНАЯ РЕГРЕССИЯ Линейная регрессия и методы ее исследования и оценки не имели бы столь большого значения, если бы помимо этого весьма важного, но все же простейшего случая, мы не получали с их помощью инструмента анализа более сложных нелинейных зависимостей. Нелинейные регрессии могут быть разделены на два существенно различных класса. Первым и более простым является класс нелинейных зависимостей, в которых имеется нелинейность относительно объясняющих переменных, но которые остаются линейными по входящим в них и подлежащим оценке параметрам. Сюда входят полиномы различных степеней и равносторонняя гипербола. Такая нелинейная регрессия по включенным в объяснение переменным простым преобразованием (заменой) переменных легко сводится к обычной линейной регрессии для новых переменных. Поэтому оценка параметров в этом случае выполняется просто по МНК, поскольку зависимости линейны по параметрам. Так важную роль в экономике играет нелинейная зависимость, описываемая равносторонней гиперболой: y = a +  (3.1)Ее параметры хорошо оцениваются по МНК и сама такая зависимость характеризует связь удельных расходов сырья, топлива, материалов с объемом выпускаемой продукции, временем обращением товаров и всех этих факторов с величиной товарооборота. Например, кривая Филипса характеризует нелинейное соотношение между нормой безработицы и процентом прироста заработной платы. Совершенно по другому обстоит дело с регрессией ,нелинейной по оцениваемым параметрам, например, представляемой степенной функцией, в которой сама степень (ее показатель) является параметром, или зависит от параметра. Также это может быть показательная функция, где основанием степени является параметр и экспоненциальная функция, в которой опять же показатель содержит параметр или комбинацию параметров. Этот класс в свою очередь делится на два подкласса: к одному относятся внешне нелинейные , но по существу внутренне линейные. В этом случае можно привести модель к линейному виду с помощью преобразований. Однако, если модель внутренне нелинейна, то она не может быть сведена к линейной функции. Таким образом, только модели внутренне нелинейные в регрессионном анализе считаются действительно нелинейными. Все прочие, сводящиеся к линейным посредством преобразований, таковыми не считаются и именно они и рассматриваются чаще всего в эконометрических исследованиях . В то же время это не означает невозможности исследования в эконометрике существенно нелинейных зависимостей. Если модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные процедуры, успешность которых зависит от вида уравнения особенностей применяемого итеративного метода. Вернемся к зависимостям, приводимым к линейным. Если они нелинейны и по параметрам и по переменным, например, вида у=а умноженному на степень х, показатель которой и есть параметр – (бета): y = a  (3.2)Очевидно, такое соотношение легко преобразуется в линейное уравнение простым логарифмированием:  .После введения новых переменных, обозначающих логарифмы, получается линейное уравнение. Тогда процедура оценивания регрессии состоит в вычислении новых переменных для каждого наблюдения путем взятия логарифмов от исходных значений. Затем оценивается регрессионная зависимость новых переменных. Для перехода к исходным переменным следует взять антилогарифм, т. е фактически вернуться к самим степеням вместо их показателей (ведь логарифм это и есть показатель степени). Аналогично может рассматриваться случай показательных или экспоненциальных функций. Для существенно нелинейной регрессии невозможно применение обычной процедуры оценивания регрессии, поскольку соответствующая зависимость не может быть преобразована в линейную. Общая схема действий при этом такова:
Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрике широко используется степенная функция. Параметр b в ней имеет четкое истолкование, являясь коэффициентом эластичности. В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, МНК применяется к преобразованным уравнениям. Практическое применение логарифмирования и соответственно экспоненты возможно тогда, когда результативный признак не имеет отрицательных значений. При исследовании взаимосвязей среди функций, использующих логарифм результативного признака, в эконометрике преобладают степенные зависимости (кривые спроса и предложения, производственные функции, кривые освоения для характеристики связи между трудоемкостью продукции, масштабами производства, зависимость ВНД от уровня занятости, кривые Энгеля). Иногда используется так называемая обратная модель, являющаяся внутренне нелинейной, но в ней в отличие от равносторонней гиперболы преобразованию подвергается не объясняющая переменная, а результативный признак у. Поэтому обратная модель оказывается внутренне нелинейной и требование МНК выполняется не для фактических значений результативного признака у, а для их обратных значений. Особого внимания заслуживает исследование корреляции для нелинейной регрессии. В общем случае парабола второй степени, также, как и полиномы более высокого порядка, при линеаризации принимает вид уравнения множественной регрессии. Если же нелинейное относительно объясняемой переменной уравнение регрессии при линеаризации принимает форму линейного уравнения парной регрессии, то для оценки тесноты связи может быть использован линейный коэффициент корреляции. Если преобразования уравнения регрессии в линейную форму связаны с зависимой переменной (результативным признаком), то линейный коэффициент корреляции по преобразованным значениям признаков дает лишь приближенную оценку связи и численно не совпадает с индексом корреляции. Следует иметь в виду, что при расчете индекса корреляции используются суммы квадратов отклонений результативного признака у, а не их логарифмов. Оценка значимости индекса корреляции выполняется также как и оценка надежности (значимости) коэффициента корреляции. Сам индекс корреляции как и индекс детерминации используется для проверки значимости в целом уравнения нелинейной регрессии по F-критерию Фишера. Отметим, что возможность построения нелинейных моделей, как посредством приведения их к линейному виду, так и путем использования нелинейной регрессии с одной стороны повышает универсальность регрессионного анализа. А с другой – существенно усложняет задачи исследователя. Если ограничиваться парным регрессионным анализом, то можно построить график наблюдений у и х как диаграмму разброса. Часто несколько различных нелинейных функций приблизительно соответствуют наблюдениям, если они лежат на некоторой кривой. Но в случае множественного регрессионного анализа такой график построить невозможно. При рассмотрении альтернативных моделей с одним и тем же определением зависимой переменной процедура выбора сравнительно проста. Можно оценивать регрессию на основе всех вероятных функций, которые можно вообразить и выбирать функцию, в наибольшей степени объясняющую изменения зависимой переменной. Понятно, что когда линейная функция объясняет примерно 64% дисперсии у, а гиперболическая - 99,9% , очевидно следует выбирать последнюю модель. Но когда разные модели используют разные функциональные формы, проблема выбора модели существенно осложняется. Более общим образом при рассмотрении альтернативных моделей с одним и тем же определением зависимой переменной выбор прост. Разумнее всего оценивать регрессию на основе всех вероятных функций, останавливаясь на функции, в наибольшей степени объясняющей изменения зависимой переменной. Если коэффициент детерминации измеряет в одном случае объясненную регрессией долю дисперсии, а в другом – объясненную регрессией долю дисперсии логарифма этой зависимой переменной, то выбор делается без затруднений. Другое дело, когда эти значения для двух моделей весьма близки и проблема выбора существенно осложняется. Тогда следует применять стандартную процедуру в виде теста Бокса-Кокса. Если нужно всего лишь сравнить модели с использованием результативного фактора и его логарифма в виде варианта зависимой переменой, то применяют вариант теста Зарембки. В нем предлагается преобразование масштаба наблюдений у, при котором обеспечивается возможность непосредственного сравнения среднеквадратичной ошибки (СКО) в линейной и логарифмическоймоделях. Соответствующая процедура включает следующие шаги:
|