Тогда уравнение парной линейной регрессии, связывающая величину ежемесячной пенсии у с величиной прожиточного минимума х, имеет вид 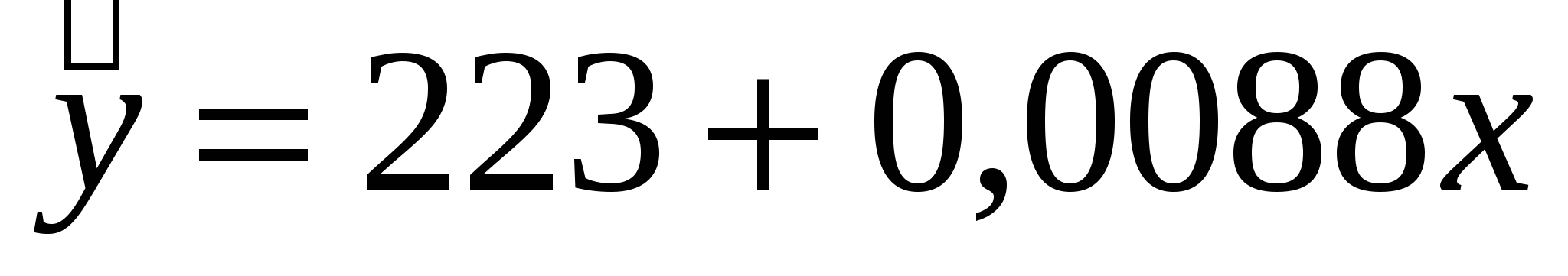 . (1.2) . (1.2) Далее, в соответствии с заданием необходимо оценить тесноту статистической связи между величиной прожиточного минимума х и величиной ежемесячной пенсии у. Эту оценку можно сделать с помощью коэффициента корреляции 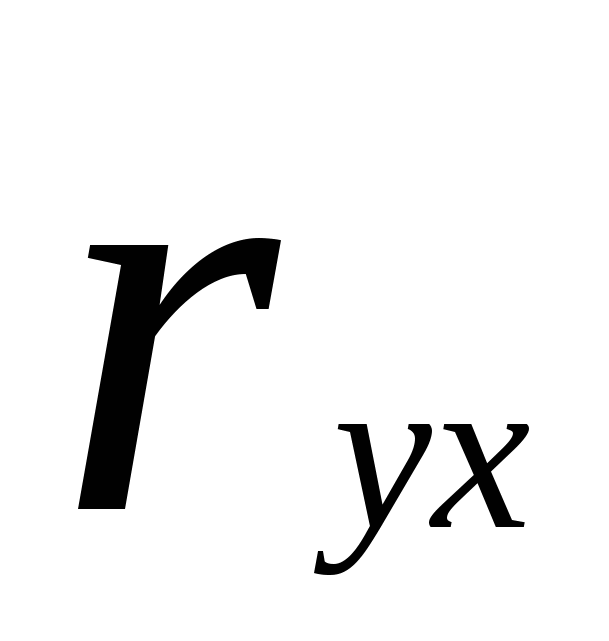 . Величина этого коэффициента на рисунке 1.4. обозначена как множественный R и соответственно равна =0,038. Поскольку теоретически величина данного коэффициента находится в пределах от –1 до +1, то можно сделать вывод о не существенности статистической связи между величиной прожиточного минимума х и величиной ежемесячной пенсии у. Параметр «R – квадрат», представленный на рисунке 5 представляет собой квадрат коэффициента корреляции . Величина этого коэффициента на рисунке 1.4. обозначена как множественный R и соответственно равна =0,038. Поскольку теоретически величина данного коэффициента находится в пределах от –1 до +1, то можно сделать вывод о не существенности статистической связи между величиной прожиточного минимума х и величиной ежемесячной пенсии у. Параметр «R – квадрат», представленный на рисунке 5 представляет собой квадрат коэффициента корреляции 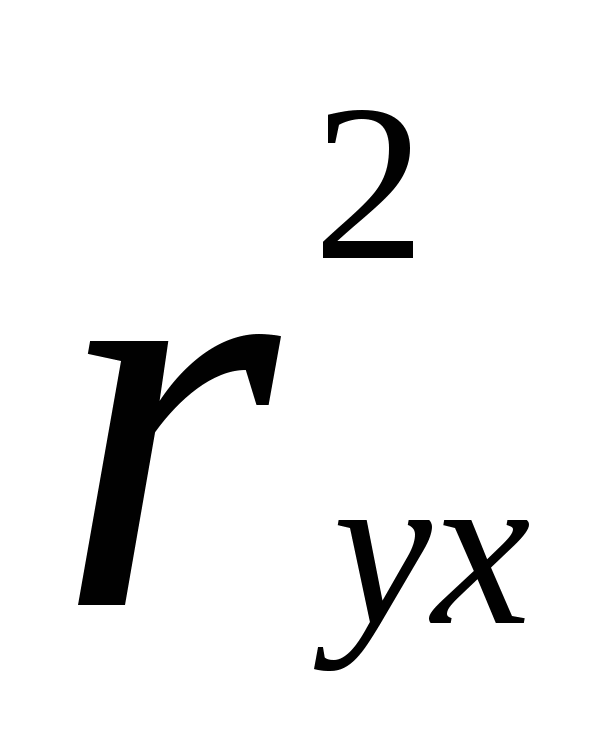 и называется коэффициентом детерминации. Величина данного коэффициента характеризует долю дисперсии зависимой переменной у, объясненную регрессией (объясняющей переменной х). Соответственно величина 1- и называется коэффициентом детерминации. Величина данного коэффициента характеризует долю дисперсии зависимой переменной у, объясненную регрессией (объясняющей переменной х). Соответственно величина 1- 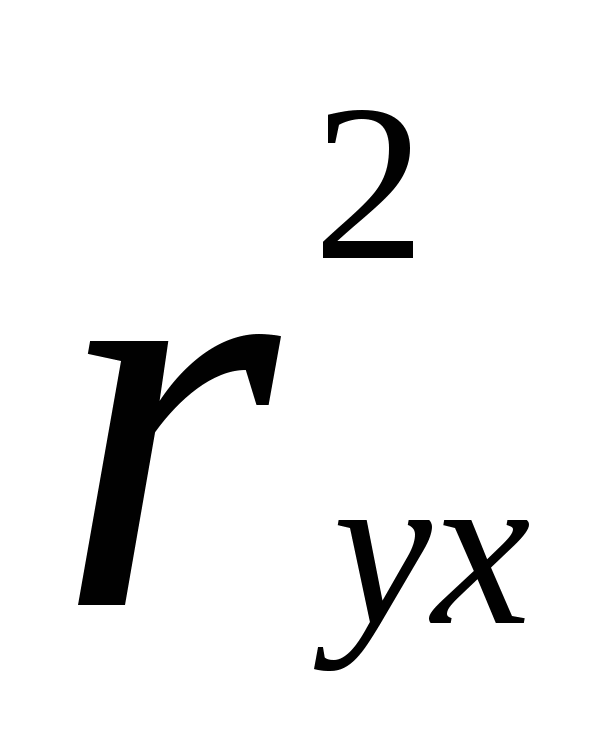 характеризует долю дисперсии переменной у, вызванную влиянием всех остальных, неучтенных в эконометрической модели объясняющих переменных. Из рисунка 5 видно, что доля всех неучтенных в полученной эконометрической модели объясняющих переменных приблизительно составляет 1- 0,00145 = 0,998 или 99,8%. характеризует долю дисперсии переменной у, вызванную влиянием всех остальных, неучтенных в эконометрической модели объясняющих переменных. Из рисунка 5 видно, что доля всех неучтенных в полученной эконометрической модели объясняющих переменных приблизительно составляет 1- 0,00145 = 0,998 или 99,8%.
На следующем этапе, в соответствии с заданием необходимо определить степень связи объясняющей переменной х с зависимой переменной у, используя коэффициент эластичности. Коэффициент эластичности для модели парной линейной регрессии определяется в виде:
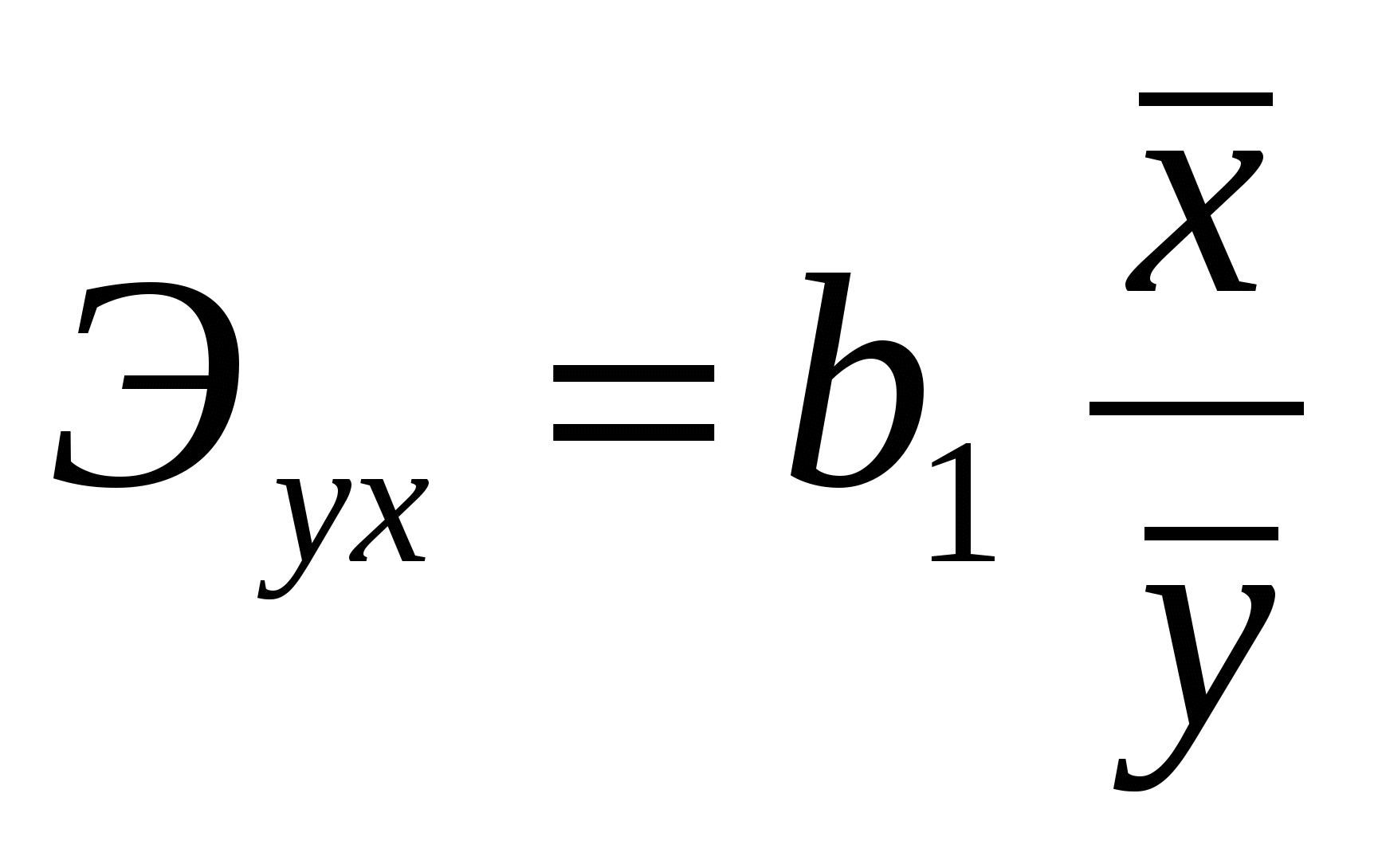 . (1.3) . (1.3)
Тогда 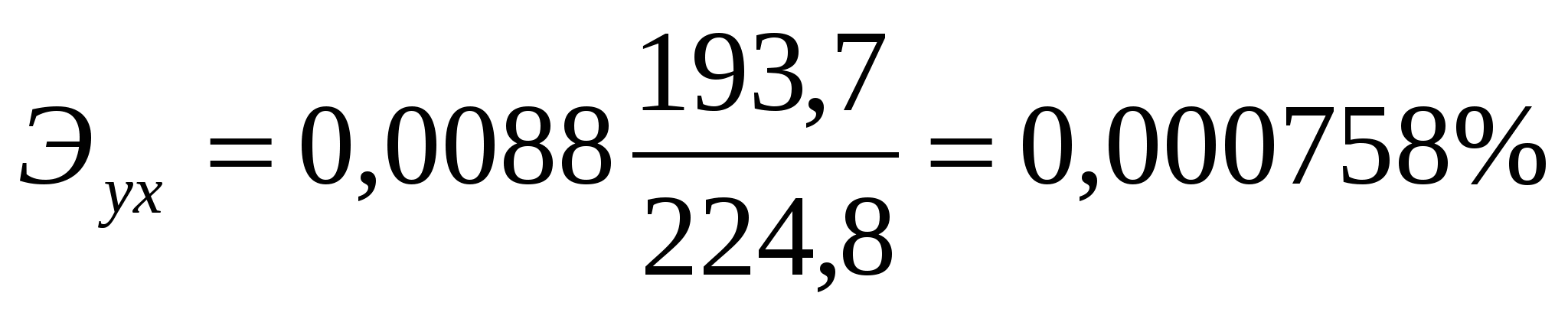
Следовательно, при изменении прожиточного минимума на 1% величина ежемесячной пенсии изменяется на 0,000758%.
Далее определяем среднюю ошибку аппроксимации по зависимости
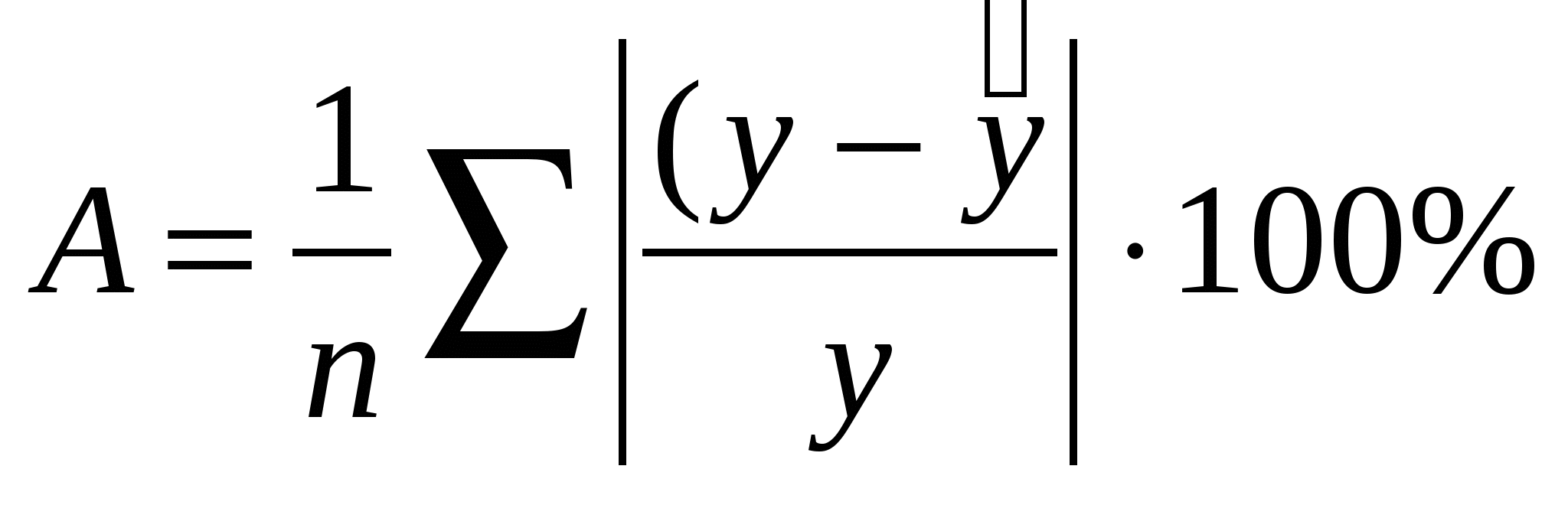 (1.4) (1.4)
Для этого исходную таблицу 1 дополняем двумя колонками, в которых определяем значения,  рассчитанные с использованием зависимости (3.1.2) и значения разности рассчитанные с использованием зависимости (3.1.2) и значения разности 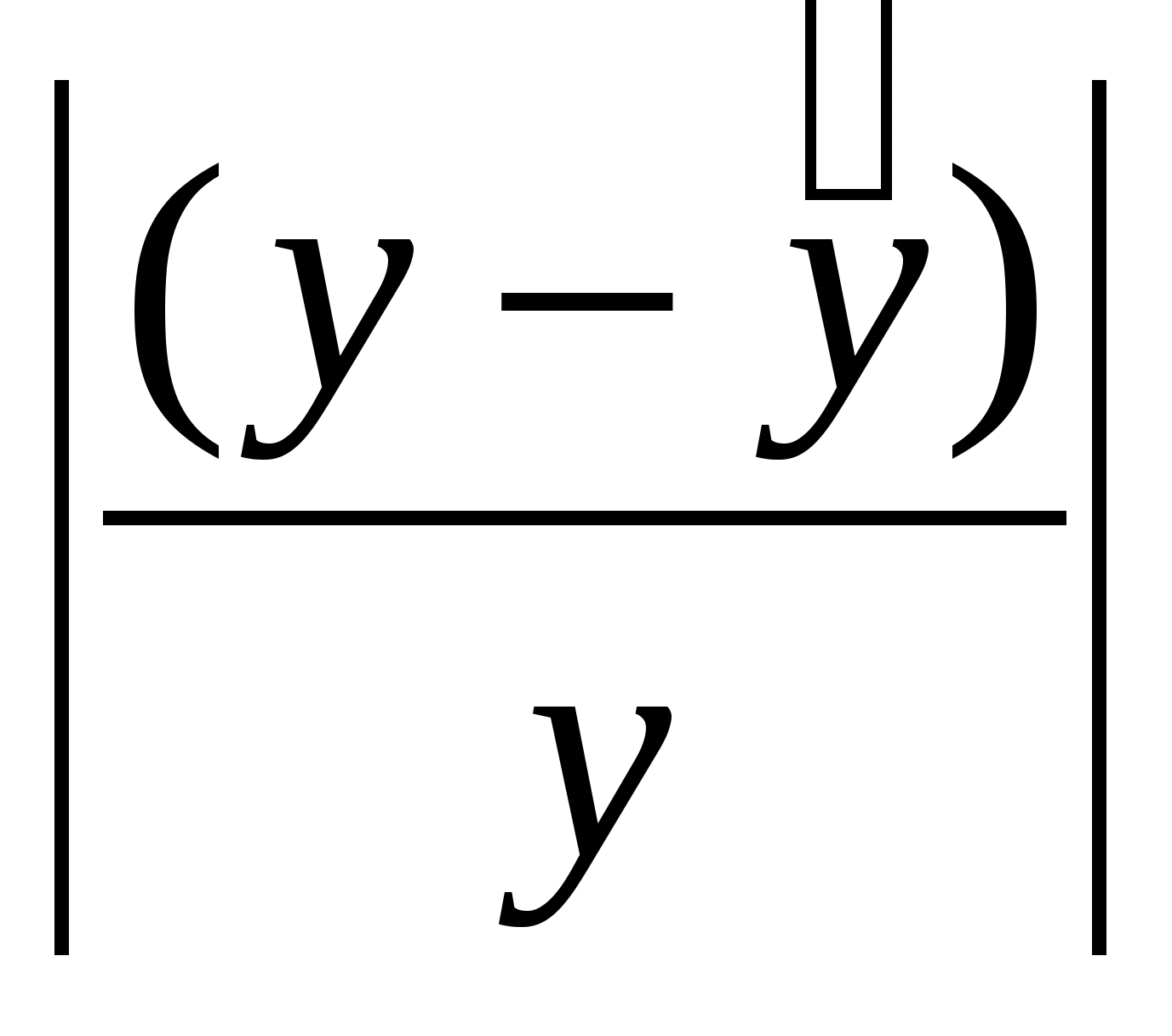 . .
Таблица 1.2. Расчет средней ошибки аппроксимации
№
п/п
|
Область
|
Средний размер назначенных ежемесячных пенсий, у.д.е.,
у
|
Прожиточный минимум в среднем на одного пенсионера в месяц, у.д.е., х
|

|
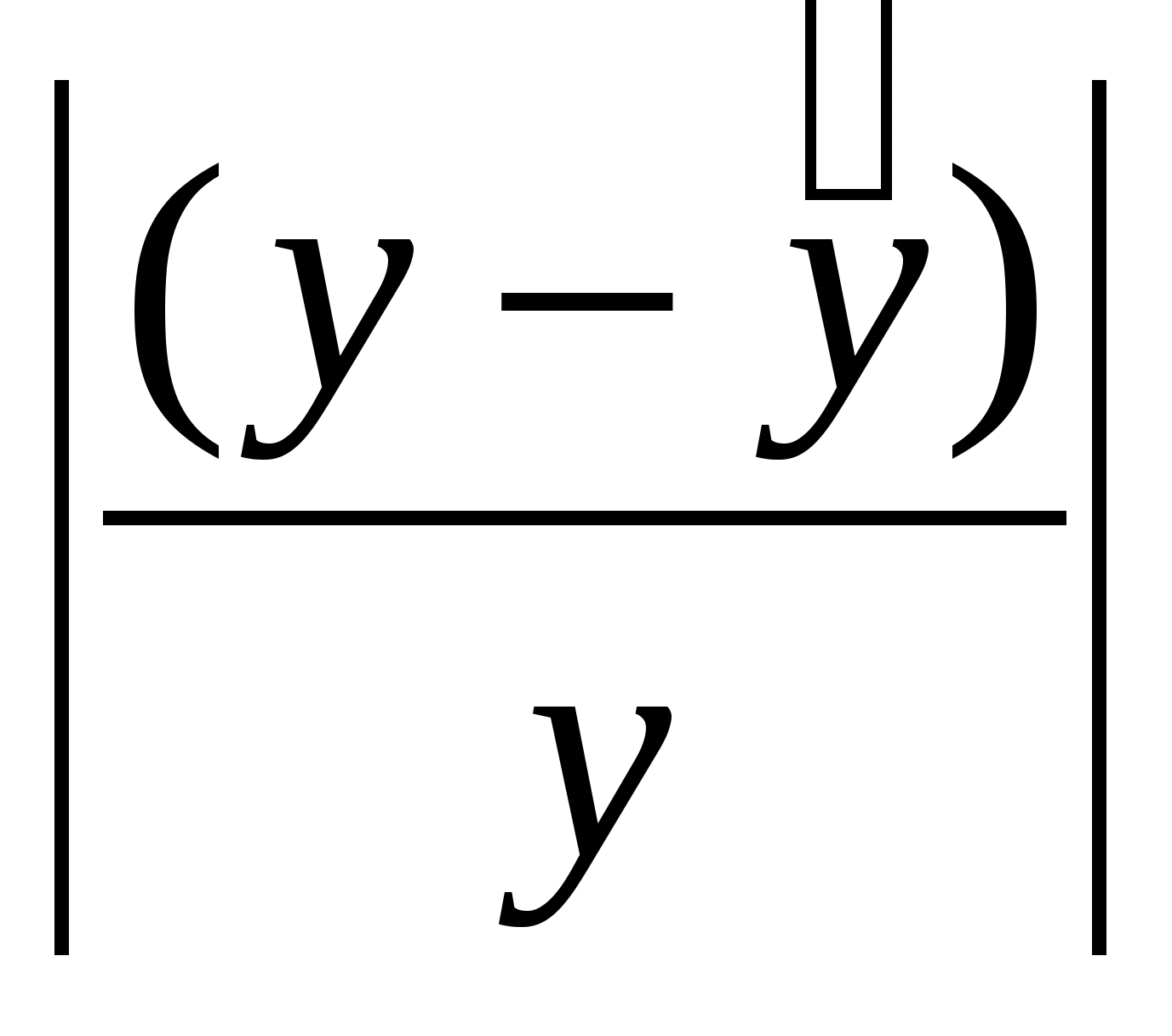
|
1
|
Орловская
|
232
|
166
|
224
|
0,032
|
2
|
Рязанская
|
215
|
199
|
225
|
0,045
|
3
|
Смоленская
|
220
|
180
|
225
|
0,021
|
4
|
Тверская
|
222
|
181
|
225
|
0,012
|
5
|
Тульская
|
231
|
186
|
225
|
0,028
|
6
|
Ярославская
|
229
|
250
|
225
|
0,017
|
|
|
|
|
|
S=0,155
| |
 Скачать 0.78 Mb.
Скачать 0.78 Mb.