Документ 21. Степеннопоказательная функция
 Скачать 281.24 Kb.
|
Степенно-показательная функция – это функция, имеющая вид степенной функции y = uv, у которой основание u и показатель степени v являются некоторыми функциями от переменной x: u = u(x); v = v(x). Эту функцию также называют показательно-степенной или сложной показательной функцией. Заметим, что степенно-показательную функцию можно представить в показательном виде:  Поэтому ее также называют сложной показательной функцией. Далее мы покажем, что производная степенно-показательной функции определяется по формуле:  Найдем производную степенно-показательной функции  где  и  есть функции от переменной  .Для этого логарифмируем уравнение (2), используя свойство логарифма:  Дифференцируем по переменной x:  Применяем правила дифференцирования сложной функции и произведения:  Подставляем в (3):  Отсюда  Итак, мы нашли производную степенно-показательной функции:  Если показатель степени  являются постоянной, то  Тогда производная равна производной сложной степенной функции: Если основание степени  являются постоянной, то  Тогда производная равна производной сложной показательной функции: Когда  и  являются функциями от x, то производная степенно-показательной функции равна сумме производных сложной степенной и показательной функций.Вычисление производной приведением к сложной показательной функции. Теперь найдем производную степенно-показательной функции  представив ее как сложную показательную функцию:  Дифференцируем произведение:  Применяем правило нахождения производной сложной функции:  И мы снова получили формулу (1). Пример 1. Найти производную следующей функции:  Решение: Вычисляем с помощью логарифмической производной. Логарифмируем исходную функцию: 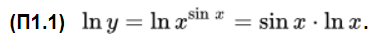 Из таблицы производных находим:  По формуле производной произведения имеем:  Дифференцируем (П1.1):  Поскольку  То  Ответ:  Пример 2. Найдите производную функции  Решение: Логарифмируем исходную функцию:  Из таблицы производных находим:  Применяем правило дифференцирования сложной функции:  Дифференцируем (П2.1), применяя формулу производной произведения двух функций: 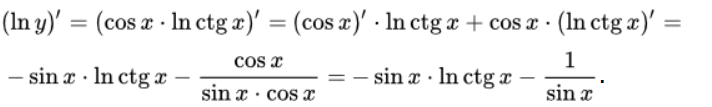 Поскольку  То  Ответ: 
|