лабораторная 1 по тмм военмех. лаба 1 по тмм военмех. Структурный и кинематический анализ плоского рычажного механизма
 Скачать 474.99 Kb. Скачать 474.99 Kb.
|
|
БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ВОЕНМЕХ» им. Д. Ф. УСТИНОВА Лабораторная работа № 1 Тема: Структурный и кинематический анализ плоского рычажного механизма. Выполнил Группа Е292 Проверил Санкт-Петербург 2021 Лабораторная работа №1. Структурный и кинематический анализ плоского рычажного механизма. Структурный анализ механизма. 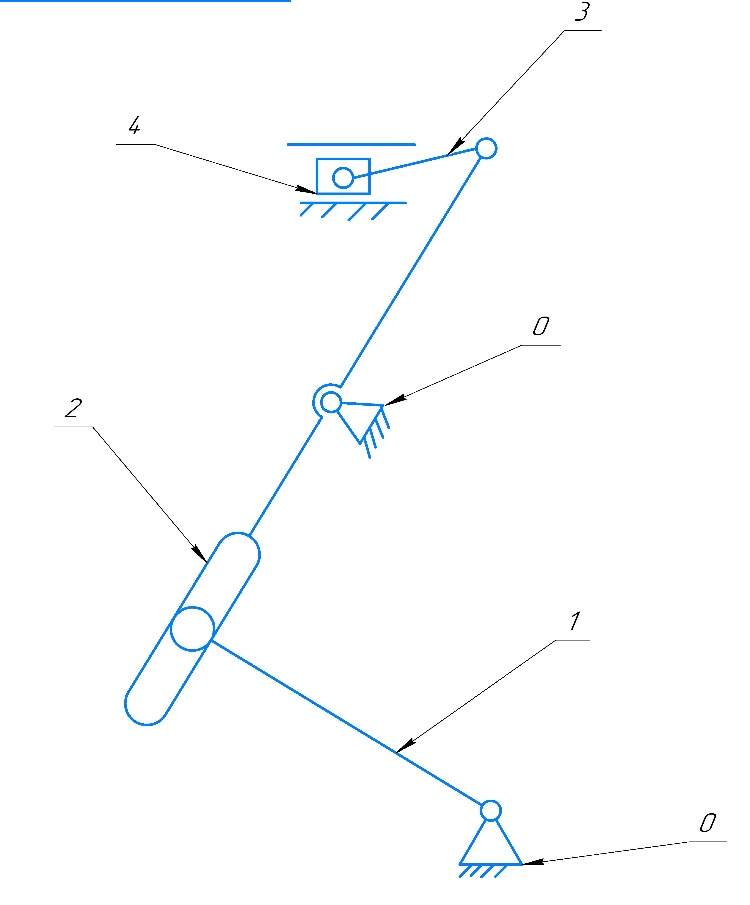 0-стойка, 1-кривошип, 2-коромысло, 3-шатун, 4-ползун. Звенья этого механизма образуют 6 кинематических пар, 5 из которых 5-го класса, а одна 4-го класса. 1-0 (5 класс) 1-2 (4 класс) 2-0 (5 класс) 2-3 (5 класс) 3-4 (5 класс) 4-0 (5 класс) Число степеней свободы по формуле Чебышева для плоских механизмов равна 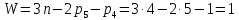 Где число n – число подвижных звеньев, а числа 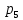 и и 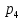 – количество кинематических пар 5 и 4 класса. – количество кинематических пар 5 и 4 класса.Кинематический анализ механизма.  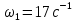 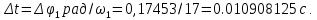 Где 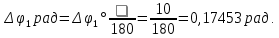 Аппроксимация функции положения тригонометрическим рядом Фурье. В этом случае функцию S(t) разлагаем в тригонометрический ряд Фурье и дифференцированием ряда определяем зависимости скорости v(t) и ускорения, а(t) ползуна. При этом необходимо решить вопрос об оптимальном числе членов ряда. Разложение функции в такой ряд означает еѐ приближенную замену тригонометрическим полиномом, являющимся суммой ряда: 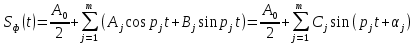 где Aj , Bj – коэффициенты ряда, pj = 2πj/T – частоты, по которым производится разложение, T = 2π/ 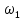 =2π/60=0,105 с – время полного оборота кривошипа =2π/60=0,105 с – время полного оборота кривошипа 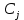 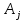 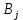 – амплитуда j-й гармоники, – амплитуда j-й гармоники, 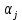 – еѐ фаза, m – число членов ряда. В данном случае функция S(t) задана таблицей значений в конечном числе точек n = 36, поэтому максимальное число членов ряда – еѐ фаза, m – число членов ряда. В данном случае функция S(t) задана таблицей значений в конечном числе точек n = 36, поэтому максимальное число членов ряда 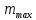 = n/2 = 36/2 = 18. = n/2 = 36/2 = 18.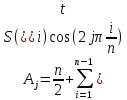 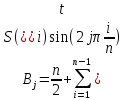 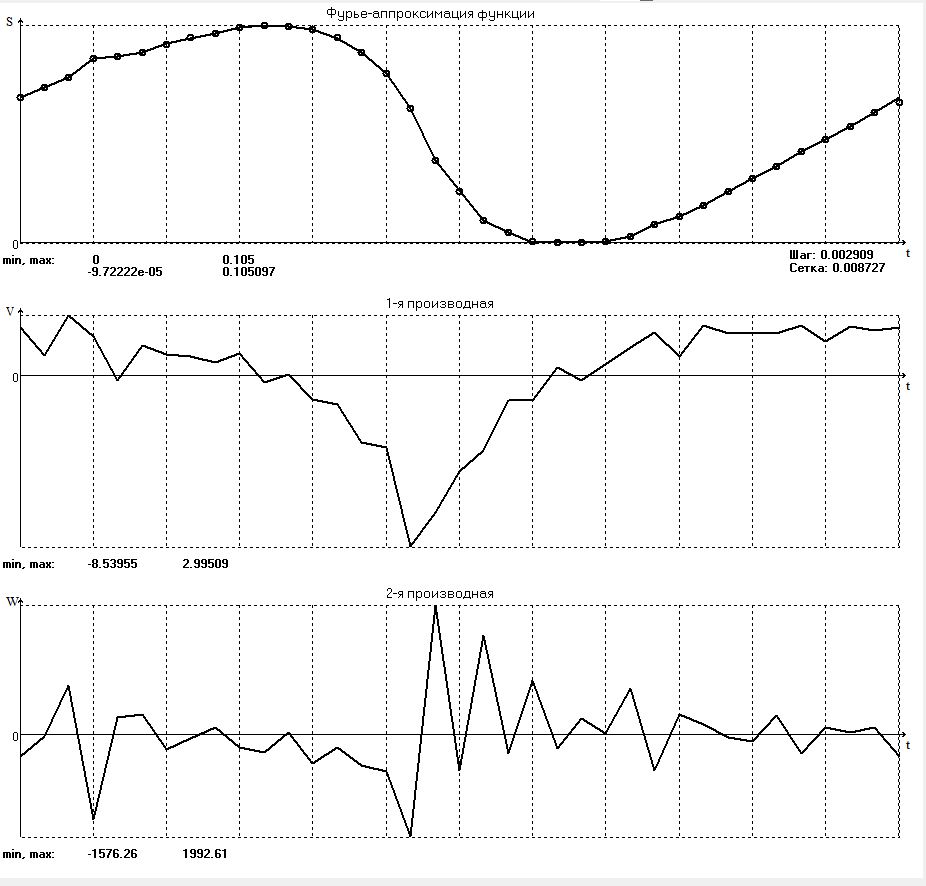 i t, c S, м Sф, м V м/c a м/с^2 0 0.000e+00 7.000e-02 7.010e-02 6.493e-01 -2.507e+01 1 1.091e-02 7.500e-02 7.490e-02 2.715e-01 -2.290e+00 2 2.182e-02 8.000e-02 8.010e-02 7.987e-01 5.380e+01 3 3.272e-02 8.900e-02 8.890e-02 5.220e-01 -9.301e+01 4 4.363e-02 9.000e-02 9.010e-02 -7.781e-02 1.866e+01 5 5.454e-02 9.200e-02 9.190e-02 4.094e-01 2.288e+01 6 6.545e-02 9.600e-02 9.610e-02 2.853e-01 -1.665e+01 7 7.636e-02 9.900e-02 9.890e-02 2.531e-01 -4.860e+00 8 8.726e-02 1.010e-01 1.011e-01 1.732e-01 8.084e+00 9 9.817e-02 1.040e-01 1.039e-01 2.999e-01 -1.431e+01 10 1.091e-01 1.050e-01 1.051e-01 -9.494e-02 -2.019e+01 11 1.200e-01 1.045e-01 1.044e-01 1.715e-02 2.716e+00 12 1.309e-01 1.030e-01 1.031e-01 -3.302e-01 -3.217e+01 13 1.418e-01 9.900e-02 9.890e-02 -3.970e-01 -1.506e+01 14 1.527e-01 9.200e-02 9.210e-02 -8.974e-01 -3.449e+01 15 1.636e-01 8.200e-02 8.190e-02 -9.676e-01 -4.151e+01 16 1.745e-01 6.500e-02 6.510e-02 -2.277e+00 -1.121e+02 17 1.854e-01 4.000e-02 3.990e-02 -1.825e+00 1.417e+02 18 1.963e-01 2.500e-02 2.510e-02 -1.278e+00 -4.004e+01 19 2.073e-01 1.100e-02 1.090e-02 -1.003e+00 1.091e+02 20 2.182e-01 5.000e-03 5.097e-03 -3.412e-01 -2.092e+01 21 2.291e-01 5.000e-04 4.028e-04 -3.379e-01 6.006e+01 22 2.400e-01 0.000e+00 9.722e-05 1.171e-01 -1.597e+01 23 2.509e-01 0.000e+00 -9.722e-05 -7.182e-02 1.776e+01 24 2.618e-01 5.000e-04 5.972e-04 1.541e-01 2.045e+00 25 2.727e-01 3.000e-03 2.903e-03 3.776e-01 5.122e+01 26 2.836e-01 9.000e-03 9.097e-03 5.709e-01 -3.940e+01 27 2.945e-01 1.300e-02 1.290e-02 2.577e-01 2.247e+01 28 3.054e-01 1.800e-02 1.810e-02 6.643e-01 1.123e+01 29 3.163e-01 2.500e-02 2.490e-02 5.606e-01 -4.059e+00 30 3.272e-01 3.100e-02 3.110e-02 5.610e-01 -8.694e+00 31 3.382e-01 3.700e-02 3.690e-02 5.666e-01 2.092e+01 32 3.491e-01 4.400e-02 4.410e-02 6.657e-01 -2.084e+01 33 3.600e-01 5.000e-02 4.990e-02 4.614e-01 8.684e+00 34 3.709e-01 5.600e-02 5.610e-02 6.572e-01 2.409e+00 35 3.818e-01 6.300e-02 6.290e-02 6.053e-01 7.922e+00 36 3.927e-01 6.800e-02 7.010e-02 6.493e-01 -2.507e+01 Амплитудный спектр 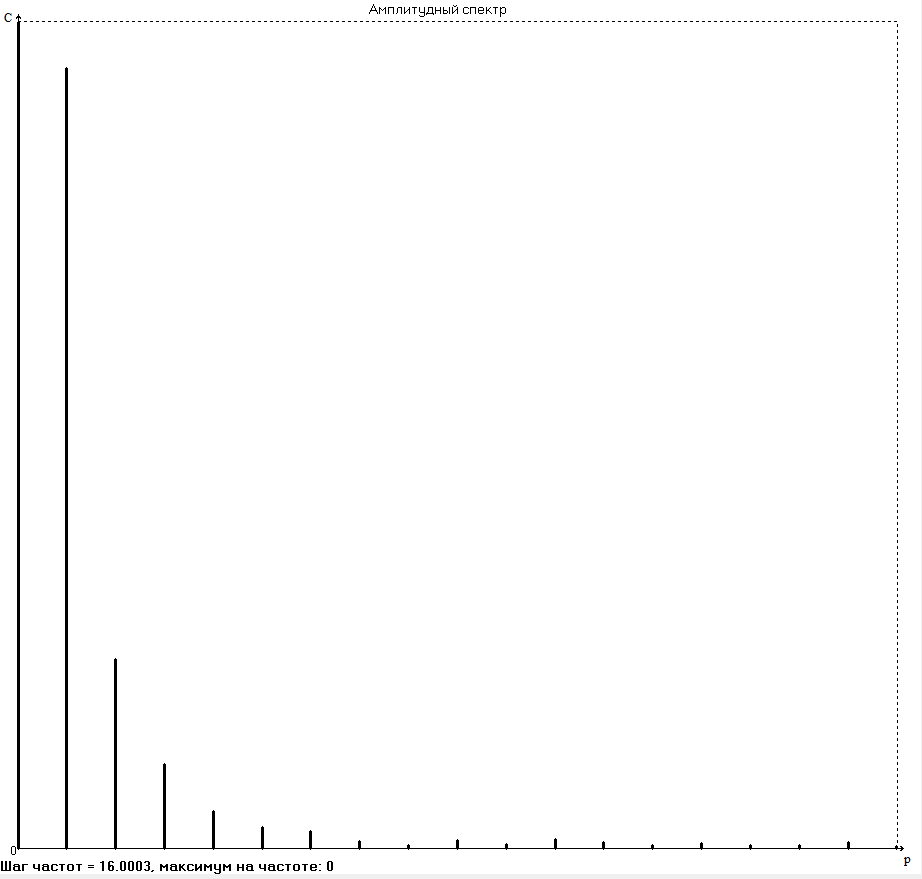 i 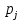 1/c p гц 1/c p гц 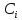 Фазы i Фазы i 0 0.000e+00 0.000e+00 5.493e-02 1 1.600e+01 2.547e+00 5.186e-02 0.3400 2 3.200e+01 5.093e+00 1.259e-02 0.3974 3 4.800e+01 7.640e+00 5.615e-03 0.7125 4 6.400e+01 1.019e+01 2.464e-03 1.2028 5 8.000e+01 1.273e+01 1.450e-03 1.0496 6 9.600e+01 1.528e+01 1.193e-03 1.4291 7 1.120e+02 1.783e+01 5.051e-04 -1.2234 8 1.280e+02 2.037e+01 2.353e-04 1.2759 9 1.440e+02 2.292e+01 5.727e-04 -0.2450 10 1.600e+02 2.547e+01 2.819e-04 0.7806 11 1.760e+02 2.801e+01 6.328e-04 -0.9143 12 1.920e+02 3.056e+01 4.204e-04 1.2806 13 2.080e+02 3.310e+01 2.142e-04 -1.0419 14 2.240e+02 3.565e+01 3.696e-04 0.7754 15 2.400e+02 3.820e+01 2.524e-04 -1.1123 16 2.560e+02 4.074e+01 2.136e-04 1.1025 17 2.720e+02 4.329e+01 4.507e-04 -1.2598 18 2.880e+02 4.584e+01 1.944e-04 1.5708 Cглаживающая аппроксимация. 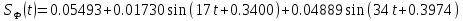 i t, c S, м Sф,м V м/c a м/с^2 0 0.000e+00 7.000e-02 7.102e-02 6.147e-01 -7.895e+00 1 1.091e-02 7.500e-02 7.721e-02 5.151e-01 -9.998e+00 2 2.182e-02 8.000e-02 8.222e-02 4.055e-01 -9.684e+00 3 3.272e-02 8.900e-02 8.611e-02 3.122e-01 -7.092e+00 4 4.363e-02 9.000e-02 8.917e-02 2.558e-01 -3.112e+00 5 5.454e-02 9.200e-02 9.186e-02 2.442e-01 8.371e-01 6 6.545e-02 9.600e-02 9.463e-02 2.683e-01 3.205e+00 7 7.636e-02 9.900e-02 9.776e-02 3.038e-01 2.763e+00 8 8.726e-02 1.010e-01 1.012e-01 3.164e-01 -1.011e+00 9 9.817e-02 1.040e-01 1.044e-01 2.710e-01 -7.716e+00 10 1.091e-01 1.050e-01 1.068e-01 1.420e-01 -1.606e+01 11 1.200e-01 1.045e-01 1.072e-01 -7.850e-02 -2.414e+01 12 1.309e-01 1.030e-01 1.048e-01 -3.761e-01 -2.988e+01 13 1.418e-01 9.900e-02 9.885e-02 -7.154e-01 -3.154e+01 14 1.527e-01 9.200e-02 8.921e-02 -1.046e+00 -2.820e+01 15 1.636e-01 8.200e-02 7.626e-02 -1.313e+00 -2.002e+01 16 1.745e-01 6.500e-02 6.097e-02 -1.469e+00 -8.189e+00 17 1.854e-01 4.000e-02 4.472e-02 -1.486e+00 5.240e+00 18 1.963e-01 2.500e-02 2.909e-02 -1.358e+00 1.788e+01 19 2.073e-01 1.100e-02 1.555e-02 -1.107e+00 2.751e+01 20 2.182e-01 5.000e-03 5.243e-03 -7.742e-01 3.262e+01 21 2.291e-01 5.000e-04 -1.236e-03 -4.136e-01 3.268e+01 22 2.400e-01 0.000e+00 -3.871e-03 -7.769e-02 2.826e+01 23 2.509e-01 0.000e+00 -3.174e-03 1.920e-01 2.085e+01 24 2.618e-01 5.000e-04 -5.966e-06 3.734e-01 1.240e+01 25 2.727e-01 3.000e-03 4.646e-03 4.659e-01 4.875e+00 26 2.836e-01 9.000e-03 9.903e-03 4.886e-01 -2.363e-01 27 2.945e-01 1.300e-02 1.516e-02 4.721e-01 -2.265e+00 28 3.054e-01 1.800e-02 2.018e-02 4.496e-01 -1.449e+00 29 3.163e-01 2.500e-02 2.505e-02 4.472e-01 1.210e+00 30 3.272e-01 3.100e-02 3.006e-02 4.775e-01 4.291e+00 31 3.382e-01 3.700e-02 3.557e-02 5.372e-01 6.386e+00 32 3.491e-01 4.400e-02 4.183e-02 6.096e-01 6.519e+00 33 3.600e-01 5.000e-02 4.883e-02 6.712e-01 4.413e+00 34 3.709e-01 5.600e-02 5.635e-02 6.995e-01 5.507e-01 35 3.818e-01 6.300e-02 6.392e-02 6.807e-01 -3.993e+00 36 3.927e-01 6.800e-02 7.102e-02 6.147e-01 -7.895e+00  Фильтрация функций с помощью скользящих средних. Скользящие средние являются одним из простейших цифровых фильтров. Сглаженная (отфильтрованная) функция получается путѐм вычисления средних арифметических значений по указанному количеству точек. При этом первые и последние точки в таблице отфильтрованной функции сохраняют свои значения. В данном исследовании функция задана в 36 точках: S0, S1, S2,…,S36. Далее мы строим скользящие средние по трѐм точкам, и отфильтрованными значениями функции будут: Sф0 = S0; Sф1 = (S0 + S1 + S2)/3; Sф2 = (S1 + S2 + S3)/3; … Sф35 = (Sn-2 + Sn-1 + Sn)/3; Sф36 = S36. 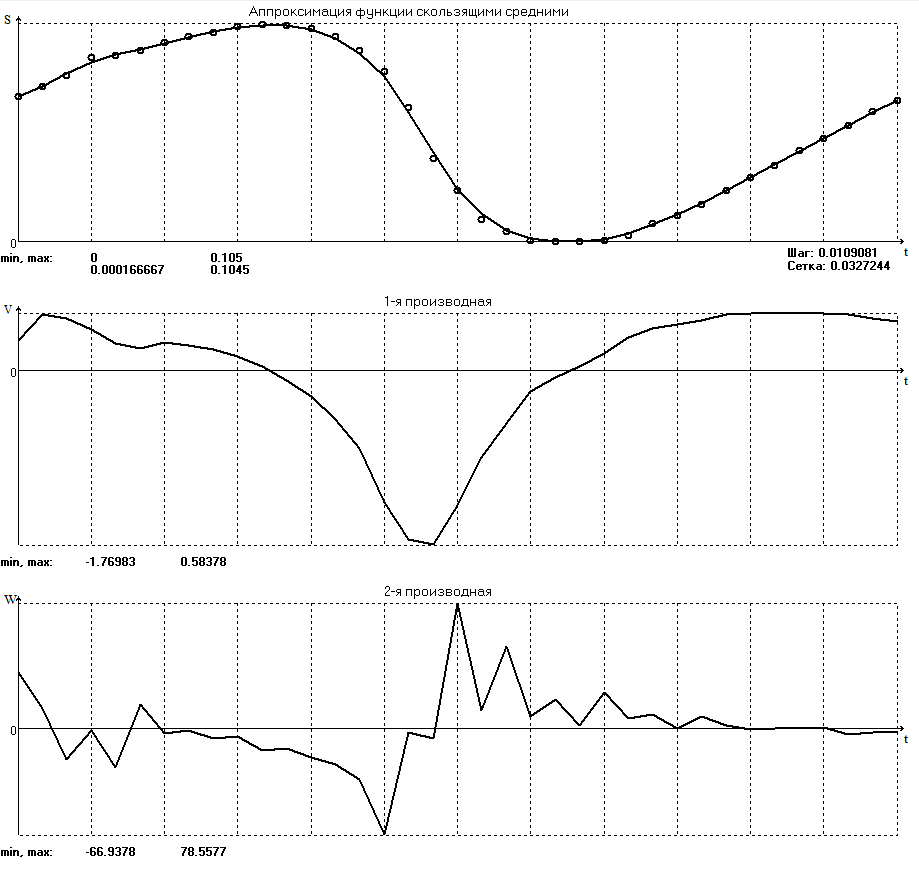 i t, c S, м Sф,м V м/c a м/с^2 0 0.000e+00 7.000e-02 7.010e-02 6.493e-01 -2.507e+01 1 1.091e-02 7.500e-02 7.490e-02 2.715e-01 -2.290e+00 2 2.182e-02 8.000e-02 8.010e-02 7.987e-01 5.380e+01 3 3.272e-02 8.900e-02 8.890e-02 5.220e-01 -9.301e+01 4 4.363e-02 9.000e-02 9.010e-02 -7.781e-02 1.866e+01 5 5.454e-02 9.200e-02 9.190e-02 4.094e-01 2.288e+01 6 6.545e-02 9.600e-02 9.610e-02 2.853e-01 -1.665e+01 7 7.636e-02 9.900e-02 9.890e-02 2.531e-01 -4.860e+00 8 8.726e-02 1.010e-01 1.011e-01 1.732e-01 8.084e+00 9 9.817e-02 1.040e-01 1.039e-01 2.999e-01 -1.431e+01 10 1.091e-01 1.050e-01 1.051e-01 -9.494e-02 -2.019e+01 11 1.200e-01 1.045e-01 1.044e-01 1.715e-02 2.716e+00 12 1.309e-01 1.030e-01 1.031e-01 -3.302e-01 -3.217e+01 13 1.418e-01 9.900e-02 9.890e-02 -3.970e-01 -1.506e+01 14 1.527e-01 9.200e-02 9.210e-02 -8.974e-01 -3.449e+01 15 1.636e-01 8.200e-02 8.190e-02 -9.676e-01 -4.151e+01 16 1.745e-01 6.500e-02 6.510e-02 -2.277e+00 -1.121e+02 17 1.854e-01 4.000e-02 3.990e-02 -1.825e+00 1.417e+02 18 1.963e-01 2.500e-02 2.510e-02 -1.278e+00 -4.004e+01 19 2.073e-01 1.100e-02 1.090e-02 -1.003e+00 1.091e+02 20 2.182e-01 5.000e-03 5.097e-03 -3.412e-01 -2.092e+01 21 2.291e-01 5.000e-04 4.028e-04 -3.379e-01 6.006e+01 22 2.400e-01 0.000e+00 9.722e-05 1.171e-01 -1.597e+01 23 2.509e-01 0.000e+00 -9.722e-05 -7.182e-02 1.776e+01 24 2.618e-01 5.000e-04 5.972e-04 1.541e-01 2.045e+00 25 2.727e-01 3.000e-03 2.903e-03 3.776e-01 5.122e+01 26 2.836e-01 9.000e-03 9.097e-03 5.709e-01 -3.940e+01 27 2.945e-01 1.300e-02 1.290e-02 2.577e-01 2.247e+01 28 3.054e-01 1.800e-02 1.810e-02 6.643e-01 1.123e+01 29 3.163e-01 2.500e-02 2.490e-02 5.606e-01 -4.059e+00 30 3.272e-01 3.100e-02 3.110e-02 5.610e-01 -8.694e+00 31 3.382e-01 3.700e-02 3.690e-02 5.666e-01 2.092e+01 32 3.491e-01 4.400e-02 4.410e-02 6.657e-01 -2.084e+01 33 3.600e-01 5.000e-02 4.990e-02 4.614e-01 8.684e+00 34 3.709e-01 5.600e-02 5.610e-02 6.572e-01 2.409e+00 35 3.818e-01 6.300e-02 6.290e-02 6.053e-01 7.922e+00 36 3.927e-01 6.800e-02 7.010e-02 6.493e-01 -2.507e+01 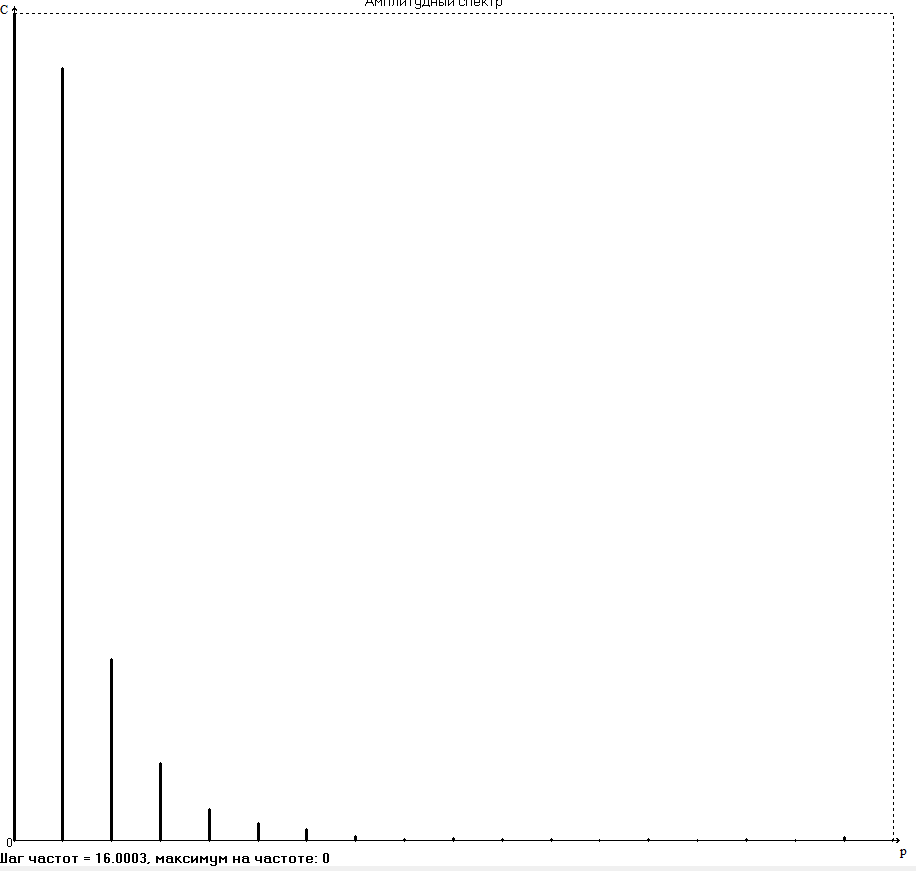 i 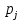 1/c p гц 1/c p гц 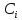 Фазы i Фазы i0 0.000e+00 0.000e+00 5.493e-02 1 1.600e+01 2.547e+00 5.134e-02 0.3400 2 3.200e+01 5.093e+00 1.207e-02 0.3977 3 4.800e+01 7.640e+00 5.131e-03 0.7108 4 6.400e+01 1.019e+01 2.063e-03 1.2120 5 8.000e+01 1.273e+01 1.130e-03 1.0337 6 9.600e+01 1.528e+01 7.727e-04 1.4668 7 1.120e+02 1.783e+01 2.975e-04 -1.3618 8 1.280e+02 2.037e+01 7.072e-05 -1.4891 9 1.440e+02 2.292e+01 1.700e-04 -0.5124 10 1.600e+02 2.547e+01 1.180e-04 0.8248 11 1.760e+02 2.801e+01 1.027e-04 -1.5136 12 1.920e+02 3.056e+01 6.415e-05 1.0472 13 2.080e+02 3.310e+01 8.050e-05 1.3442 14 2.240e+02 3.565e+01 3.017e-05 -0.7034 15 2.400e+02 3.820e+01 1.246e-04 -1.5006 16 2.560e+02 4.074e+01 2.232e-05 -0.7977 17 2.720e+02 4.329e+01 2.156e-04 -1.3930 18 2.880e+02 4.584e+01 9.259e-06 1.5708 Применение интерполяционных сплайнов Интерполяционный кубический сплайн – это совокупность полиномов третьей степени: SСi(t) = Si +bi(t – ti) +ci(t – ti) 2 +di(t – ti) 3 , где Si – значения аппроксимируемой функции в узлах, ti – значения аргумента в узлах, bi ,ci ,di – коэффициенты сплайна для i-го участка, i = 0,1,2,…n–1 – номер участка, n – число точек в таблице, считая с нуля. Построение такого сплайна состоит в определении коэффициентов bi , ci , di . Тогда для каждого i-го участка по формуле можно найти значение сплайна SСi(t) для любого ti ≤ t ≤ ti+1, которое и будет приближѐнным значением функции S(t). Дифференцированием аппроксимирующей функции определяется скорость звена; v(t) vСi(t) = bi + 2ci(t – ti) + 3di(t – ti) 2 i t, c S, м Cплaйн Произв-я 1 Произв-я 2 0 0.000e+00 7.000e-02 7.000e-02 6.380e-01 -4.414e+01 1 1.091e-02 7.500e-02 7.500e-02 3.399e-01 -1.052e+01 2 2.182e-02 8.000e-02 8.000e-02 7.528e-01 8.624e+01 3 3.272e-02 8.900e-02 8.900e-02 4.993e-01 -1.327e+02 4 4.363e-02 9.000e-02 9.000e-02 2.792e-04 4.122e+01 5 5.454e-02 9.200e-02 9.200e-02 3.247e-01 1.825e+01 6 6.545e-02 9.600e-02 9.600e-02 3.512e-01 -1.339e+01 7 7.636e-02 9.900e-02 9.900e-02 1.957e-01 -1.513e+01 8 8.726e-02 1.010e-01 1.010e-01 2.412e-01 2.348e+01 9 9.817e-02 1.040e-01 1.040e-01 2.145e-01 -2.838e+01 10 1.091e-01 1.050e-01 1.050e-01 7.386e-04 -1.082e+01 11 1.200e-01 1.045e-01 1.045e-01 -7.997e-02 -3.978e+00 12 1.309e-01 1.030e-01 1.030e-01 -2.309e-01 -2.369e+01 13 1.418e-01 9.900e-02 9.900e-02 -5.091e-01 -2.732e+01 14 1.527e-01 9.200e-02 9.200e-02 -7.580e-01 -1.831e+01 15 1.636e-01 8.200e-02 8.200e-02 -1.134e+00 -5.072e+01 16 1.745e-01 6.500e-02 6.500e-02 -2.130e+00 -1.318e+02 17 1.854e-01 4.000e-02 4.000e-02 -1.897e+00 1.744e+02 18 1.963e-01 2.500e-02 2.500e-02 -1.282e+00 -6.175e+01 19 2.073e-01 1.100e-02 1.100e-02 -9.486e-01 1.230e+02 20 2.182e-01 5.000e-03 5.000e-03 -4.237e-01 -2.675e+01 21 2.291e-01 5.000e-04 5.000e-04 -2.443e-01 5.965e+01 22 2.400e-01 0.000e+00 0.000e+00 2.569e-02 -1.015e+01 23 2.509e-01 0.000e+00 0.000e+00 4.005e-03 6.179e+00 24 2.618e-01 5.000e-04 5.000e-04 9.580e-02 1.065e+01 25 2.727e-01 3.000e-03 3.000e-03 4.379e-01 5.206e+01 26 2.836e-01 9.000e-03 9.000e-03 4.905e-01 -4.242e+01 27 2.945e-01 1.300e-02 1.300e-02 3.505e-01 1.675e+01 28 3.054e-01 1.800e-02 1.800e-02 5.828e-01 2.583e+01 29 3.163e-01 2.500e-02 2.500e-02 6.188e-01 -1.923e+01 30 3.272e-01 3.100e-02 3.100e-02 5.175e-01 6.502e-01 31 3.382e-01 3.700e-02 3.700e-02 6.117e-01 1.663e+01 32 3.491e-01 4.400e-02 4.400e-02 6.111e-01 -1.673e+01 33 3.600e-01 5.000e-02 5.000e-02 5.191e-01 -1.400e-01 34 3.709e-01 5.600e-02 5.600e-02 6.127e-01 1.729e+01 35 3.818e-01 6.300e-02 6.300e-02 6.056e-01 -1.859e+01 36 3.927e-01 6.800e-02 6.800e-02 2.653e-01 -4.380e+01 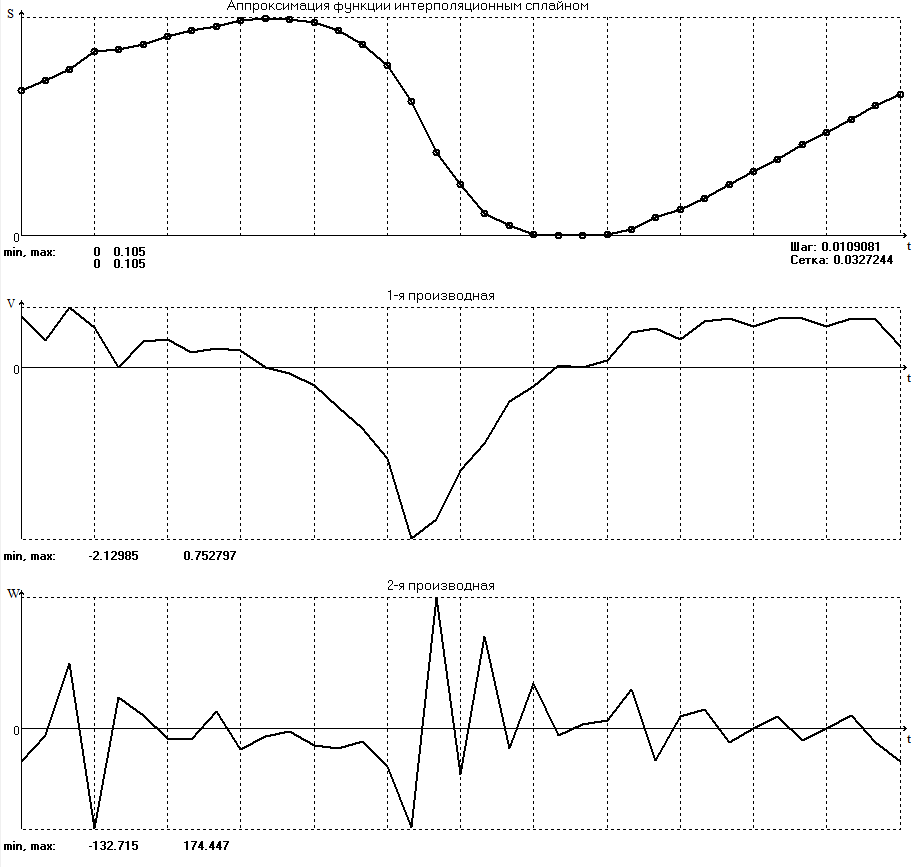 Применение сглаживающего сплайна. 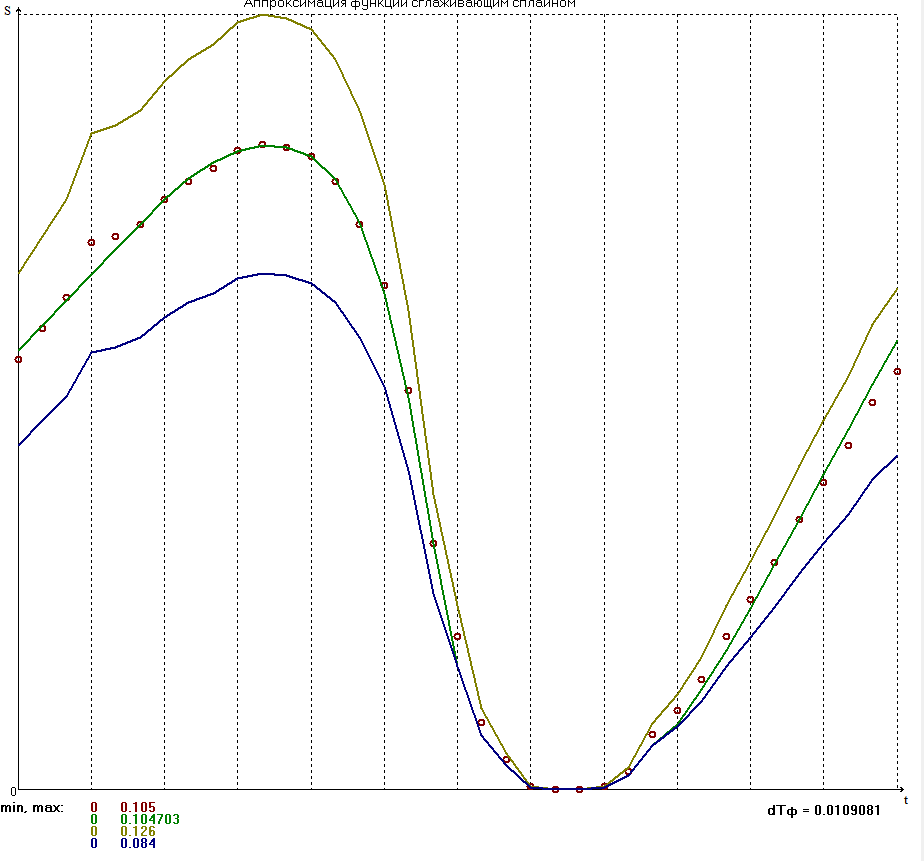 i t, c S, м Cплaйн Произв-я 1 Произв-я 2 0 0.000e+00 7.000e-02 7.139e-02 3.780e-01 1.901e-03 1 1.091e-02 7.500e-02 7.552e-02 3.780e-01 -4.936e-04 2 2.182e-02 8.000e-02 7.964e-02 3.780e-01 1.021e-04 3 3.272e-02 8.900e-02 8.376e-02 3.779e-01 -1.425e-02 4 4.363e-02 9.000e-02 8.788e-02 3.777e-01 -3.206e-02 5 5.454e-02 9.200e-02 9.200e-02 3.772e-01 -4.972e-02 6 6.545e-02 9.600e-02 9.600e-02 3.459e-01 -5.687e+00 7 7.636e-02 9.900e-02 9.942e-02 2.797e-01 -6.457e+00 8 8.726e-02 1.010e-01 1.021e-01 2.051e-01 -7.228e+00 9 9.817e-02 1.040e-01 1.039e-01 1.220e-01 -7.994e+00 10 1.091e-01 1.050e-01 1.047e-01 3.056e-02 -8.779e+00 11 1.200e-01 1.045e-01 1.045e-01 -6.910e-02 -9.494e+00 12 1.309e-01 1.030e-01 1.030e-01 -2.232e-01 -1.877e+01 13 1.418e-01 9.900e-02 9.928e-02 -4.734e-01 -2.709e+01 14 1.527e-01 9.200e-02 9.226e-02 -8.366e-01 -3.952e+01 15 1.636e-01 8.200e-02 8.080e-02 -1.263e+00 -3.864e+01 16 1.745e-01 6.500e-02 6.376e-02 -1.950e+00 -8.736e+01 17 1.854e-01 4.000e-02 4.000e-02 -2.158e+00 4.927e+01 18 1.963e-01 2.500e-02 2.004e-02 -1.442e+00 8.189e+01 19 2.073e-01 1.100e-02 8.814e-03 -6.494e-01 6.351e+01 20 2.182e-01 5.000e-03 4.009e-03 -3.691e-01 -1.212e+01 21 2.291e-01 5.000e-04 4.012e-04 -1.880e-01 4.532e+01 22 2.400e-01 0.000e+00 0.000e+00 1.843e-02 -7.479e+00 23 2.509e-01 0.000e+00 0.000e+00 3.941e-03 4.823e+00 24 2.618e-01 5.000e-04 4.002e-04 7.587e-02 8.365e+00 25 2.727e-01 3.000e-03 2.404e-03 3.538e-01 4.260e+01 26 2.836e-01 9.000e-03 7.218e-03 3.839e-01 -3.708e+01 27 2.945e-01 1.300e-02 1.067e-02 3.837e-01 3.705e+01 28 3.054e-01 1.800e-02 1.629e-02 5.756e-01 -1.874e+00 29 3.163e-01 2.500e-02 2.262e-02 6.009e-01 6.516e+00 30 3.272e-01 3.100e-02 2.948e-02 6.486e-01 2.230e+00 31 3.382e-01 3.700e-02 3.667e-02 6.681e-01 1.341e+00 32 3.491e-01 4.400e-02 4.400e-02 6.729e-01 -4.591e-01 33 3.600e-01 5.000e-02 5.132e-02 6.688e-01 -2.964e-01 34 3.709e-01 5.600e-02 5.859e-02 6.660e-01 -2.077e-01 35 3.818e-01 6.300e-02 6.585e-02 6.643e-01 -1.018e-01 36 3.927e-01 6.800e-02 7.309e-02 6.638e-01 5.724e-04 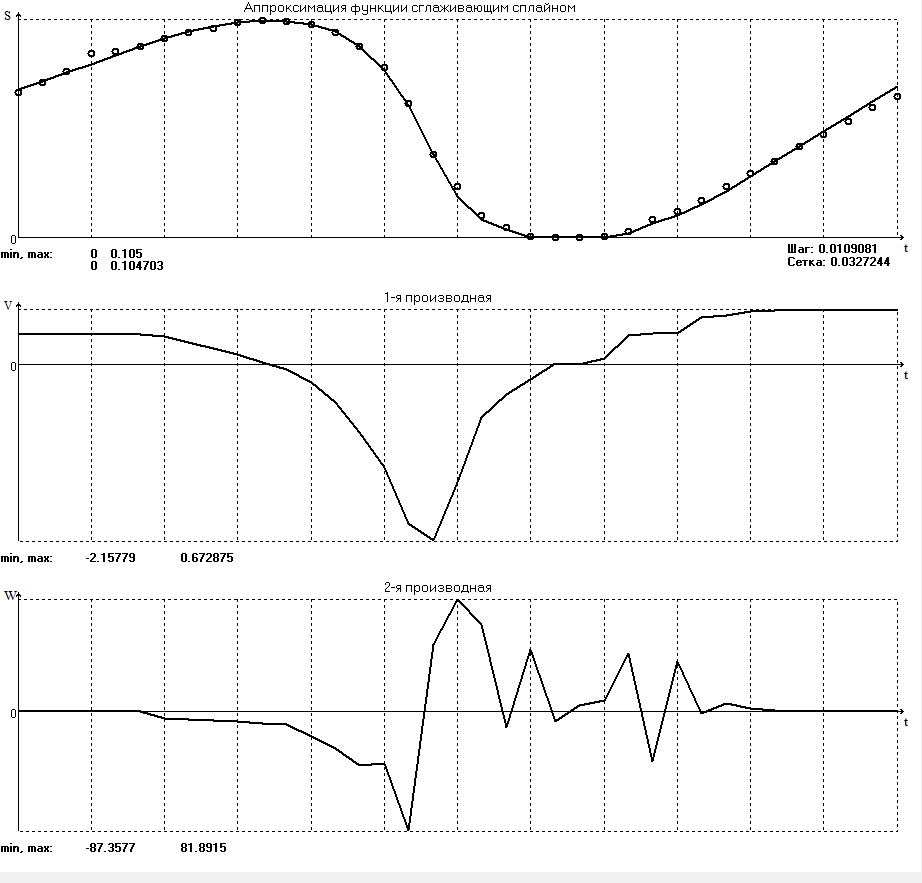 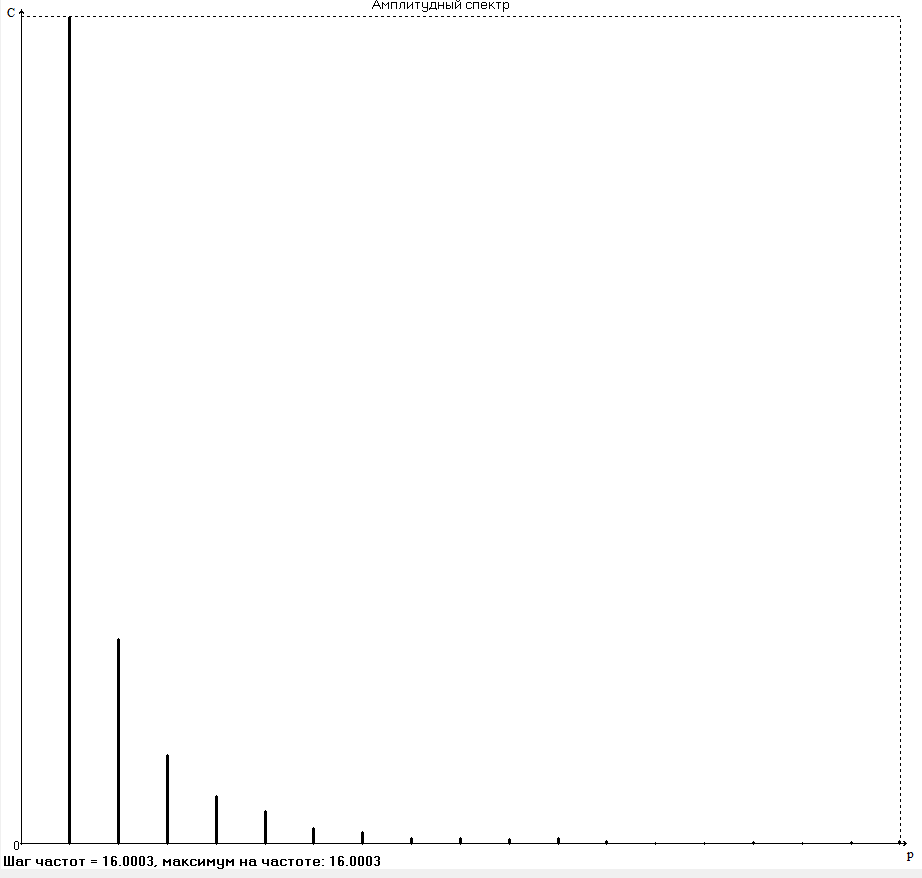 Аппроксимация функции полиномами, коэффициенты которых определены по методу наименьших квадратов (МНК). По этому методу искомую гладкую функцию строят в виде суммы простых аналитических функций, выбор которых является отдельной нетривиальной задачей. В данной программе используется самая простая – система степенных функций: 1, t, t 2 , t 3 , … . Так что нужная гладкая функция получается в виде полинома: SП(t) = b0 + b1t + b2t 2 + b3t 3 + … + bnt m , где m – задаваемая пользователем степень полинома. Таким образом, задача сводится к нахождению оптимальной степени полинома m и коэффициентов bi таких, чтобы график SП(t), проходил между точками исходной функции, минимизируя среднее квадратическое отклонение значений исходной функции от значений полинома . Исследования, проведѐнные с помощью программы ApproxFSP, показали, что оптимальная степень полинома m = 11. Функция аппроксимирована удовлетворительно, со сглаживанием. Первая производная – тоже удовлетворительно. Первая и вторая производная аппроксимирована неудовлетворительно на краях. 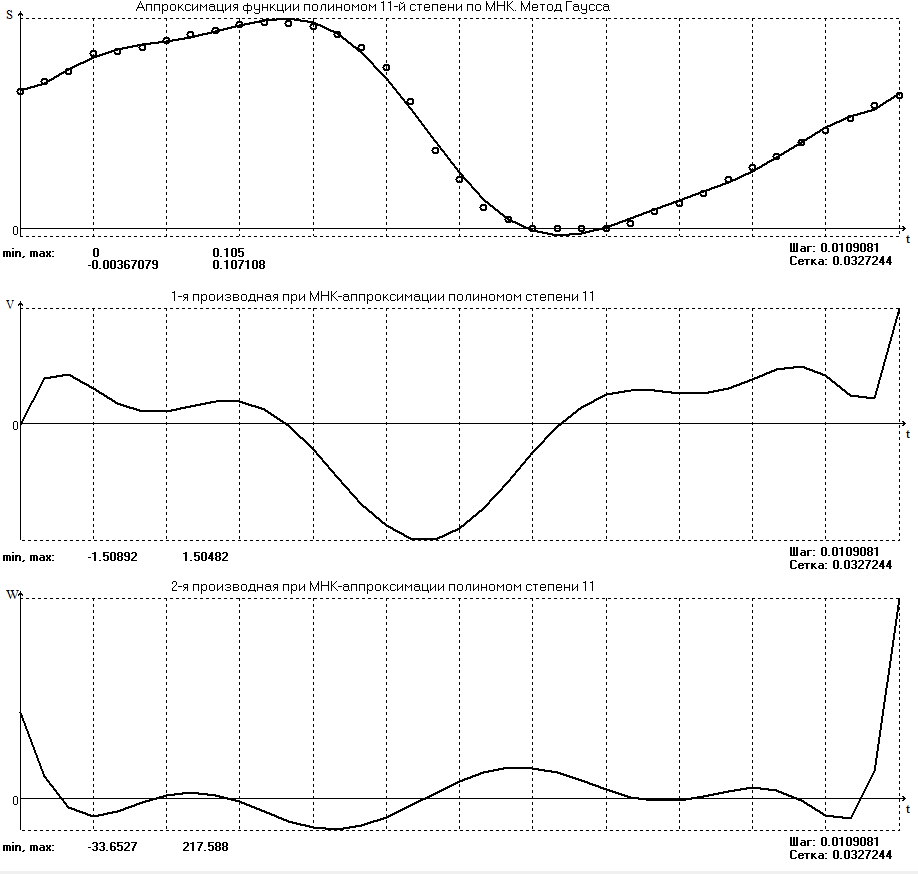 i t, c S, м Sп Произв-я 1 Произв-я 2 0 0.000e+00 7.000e-02 7.026e-02 -1.541e-02 9.342e+01 1 1.091e-02 7.500e-02 7.411e-02 5.951e-01 2.461e+01 2 2.182e-02 8.000e-02 8.122e-02 6.457e-01 -1.026e+01 3 3.272e-02 8.900e-02 8.736e-02 4.635e-01 -1.983e+01 4 4.363e-02 9.000e-02 9.129e-02 2.663e-01 -1.474e+01 5 5.454e-02 9.200e-02 9.351e-02 1.602e-01 -4.529e+00 6 6.545e-02 9.600e-02 9.518e-02 1.609e-01 3.979e+00 7 7.636e-02 9.900e-02 9.726e-02 2.269e-01 7.071e+00 8 8.726e-02 1.010e-01 1.001e-01 2.921e-01 3.883e+00 9 9.817e-02 1.040e-01 1.034e-01 2.933e-01 -4.301e+00 10 1.091e-01 1.050e-01 1.061e-01 1.894e-01 -1.491e+01 11 1.200e-01 1.045e-01 1.071e-01 -2.997e-02 -2.497e+01 12 1.309e-01 1.030e-01 1.051e-01 -3.436e-01 -3.182e+01 13 1.418e-01 9.900e-02 9.943e-02 -7.058e-01 -3.365e+01 14 1.527e-01 9.200e-02 8.978e-02 -1.057e+00 -2.980e+01 15 1.636e-01 8.200e-02 7.663e-02 -1.337e+00 -2.078e+01 16 1.745e-01 6.500e-02 6.105e-02 -1.497e+00 -8.120e+00 17 1.854e-01 4.000e-02 4.452e-02 -1.509e+00 5.967e+00 18 1.963e-01 2.500e-02 2.868e-02 -1.371e+00 1.904e+01 19 2.073e-01 1.100e-02 1.508e-02 -1.105e+00 2.887e+01 20 2.182e-01 5.000e-03 4.863e-03 -7.584e-01 3.389e+01 21 2.291e-01 5.000e-04 -1.373e-03 -3.858e-01 3.352e+01 22 2.400e-01 0.000e+00 -3.671e-03 -4.503e-02 2.825e+01 23 2.509e-01 0.000e+00 -2.640e-03 2.182e-01 1.963e+01 24 2.618e-01 5.000e-04 7.157e-04 3.795e-01 9.974e+00 25 2.727e-01 3.000e-03 5.274e-03 4.414e-01 1.826e+00 26 2.836e-01 9.000e-03 1.009e-02 4.329e-01 -2.633e+00 27 2.945e-01 1.300e-02 1.463e-02 4.015e-01 -2.306e+00 28 3.054e-01 1.800e-02 1.895e-02 3.982e-01 2.245e+00 29 3.163e-01 2.500e-02 2.355e-02 4.570e-01 8.519e+00 30 3.272e-01 3.100e-02 2.914e-02 5.754e-01 1.240e+01 31 3.382e-01 3.700e-02 3.614e-02 7.022e-01 9.405e+00 32 3.491e-01 4.400e-02 4.416e-02 7.466e-01 -2.702e+00 33 3.600e-01 5.000e-02 5.181e-02 6.249e-01 -1.943e+01 34 3.709e-01 5.600e-02 5.727e-02 3.693e-01 -2.259e+01 35 3.818e-01 6.300e-02 6.058e-02 3.295e-01 2.979e+01 36 3.927e-01 6.800e-02 6.874e-02 1.505e+00 2.176e+02 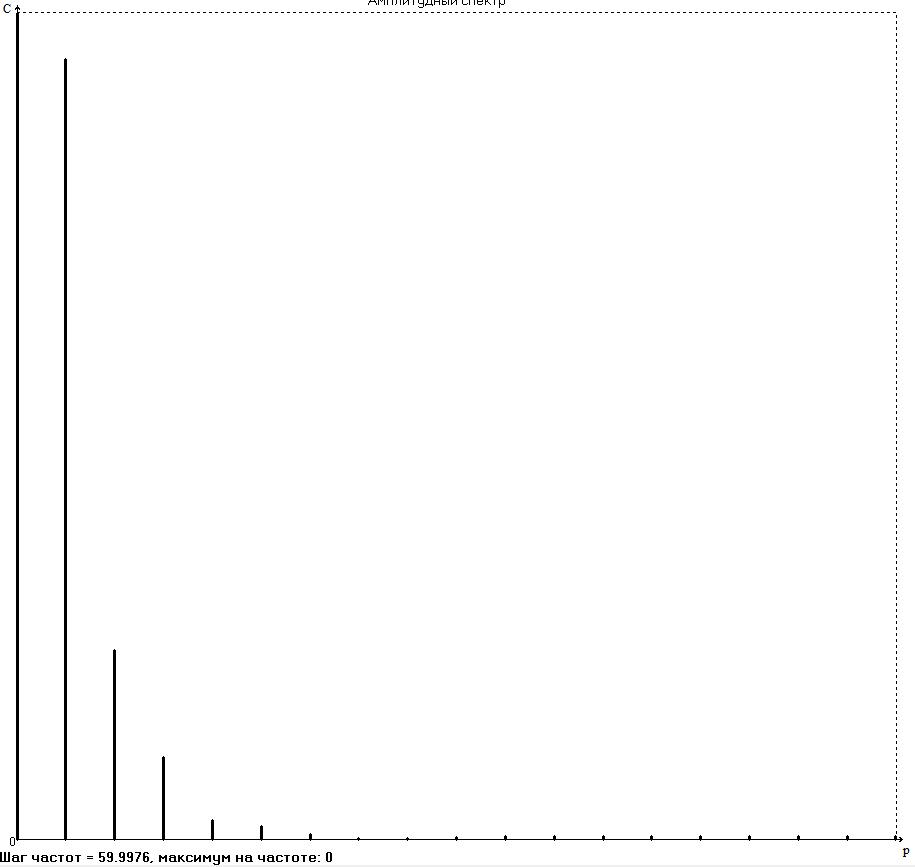 Вывод 1. Функция аппроксимировалась пятью методами, четыре из которых позволяют сглаживать функции. 2. Сглаживание может быть необходимо, например, в тех случаях, когда функция искажена погрешностями эксперимента. 2. Ряд Фурье позволяет производить как интерполирующую, так и сглаживающую аппроксимацию. Для сглаживающей аппроксимации следует при разложении учитывать лишь первые основные частоты, что определяется по амплитудному спектру. 3. Тригонометрические ряды Фурье хорошо аппроксимируют гладкие периодические функции. 4. С помощью скользящих средних удовлетворительно выполнена сглаживающая аппроксимация самой функции, несколько хуже – первой производной и неудовлетворительно – второй производной. 5. Интерполяционные сплайны целесообразно применять в тех случаях, когда аппроксимирующую функцию надо проводить в точности по исходным точкам. 6. Сглаживающий сплайн хорошо сгладил функцию и первую производную, но несколько хуже – вторую производную. Результаты сглаживания сильно зависят от конфигурации коридора. 7. Полином, построенный по МНК, хорошо сгладил функцию и первую производную, но несколько хуже – вторую производную. 8. Во всех методах кроме ряда Фурье на графиках производных начальное значение не равно конечному, в то время как функция в данном случае периодична по своей сути. 9. В данной лабораторной работе наилучшие результаты получены при аппроксимации тригонометрическим рядом Фурье. |
