Кр. Задание_на_кр. Структурный синтез дискретных автоматов
 Скачать 0.92 Mb.
|
|
ЗАДАНИЕ для выполнения расчетно-графической работы С МЕТОДИЧЕСКИМИ УКАЗАНИЯМИ «Теория дискретных устройств» (название дисциплины) Тема: «Структурный синтез дискретных автоматов» Направление/специальность: 23.05.05. Системы обеспечения движения поездов (код, наименование специальности /направления) Профиль/специализация: «Автоматика и телемеханика на железнодорожном транспорте» Квалификация (степень) выпускника: инженер путей сообщения Форма обучения: заочная ОБЩИЕ УКАЗАНИЯ Для успешного выполнения расчетно-графической (контрольной) работы студент должен иметь представление об основных функциях и законах алгебры логики, способах задания и минимизации функций алгебры логики, а также о методах синтеза комбинационных дискретных устройств и конечных автоматов. Прежде, чем приступать к выполнению, студент должен изучить соответствующие разделы основной [2] и дополнительной литературы [3, 4, 6]. Цель расчетно-графической работы - закрепить знания, полученные студентом при самостоятельном изучении дисциплины. Контрольная работа состоит из двух задач. Пояснительная записка должна содержать исходные данные по варианту, краткие пояснения к методике решения каждой задачи с приложением необходимых чертежей и таблиц. В конце пояснительной записки следует привести список использованной литературы. ЗАДАНИЕ НА КОНТРОЛЬНУЮ РАБОТУ ЗАДАЧА 1 Условия работы комбинационного устройства, имеющего четыре входа (  ) и один выход  , заданы таблицей истинности (табл.1), где индекс при соответствует номеру варианта, определяемого последней цифрой шифра студента.Требуется синтезировать функциональную логическую схему устройства в базисе И-НЕ (для четного номера варианта) и ИЛИ-НЕ (для нечетного номера варианта), применяя методы минимизации заданной логической функции с помощью алгебраических преобразований и с использованием карт Карно. Таблица 1 Таблица истинности комбинационных устройств
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАЧИ 1 Для построения функциональной логической схемы необходимо сформулировать условия ее работы и записать их в виде логической функции (ФАЛ). Синтез логической схемы включает в себя несколько этапов: задание ФАЛ в виде таблицы истинности, в которой для каждого набора значений входных переменных указывают значение функции (0 или 1); переход от таблицы истинности к структурной формуле в базисе И, ИЛИ, НЕ; минимизация ФАЛ; выбор элементной базы и запись структурной формулы минимизированной ФАЛ в выбранном базисе (И-НЕ или ИЛИ-НЕ); построение функциональной логической схемы комбинационного устройства, последовательность соединения элементов которой определяется последовательностью выполнения логических операций в структурной формуле. Таблица истинности заданной ФАЛ составляется в зависимости от варианта (табл. 1). При переходе от таблицы истинности к структурной формуле применяют два способа составления последней. Если количество наборов значений входных переменных, при которых значение функции равно 1, значительно превышает количество наборов, при которых функция принимает нулевое значение, то применяют совершенную дизъюнктивную нормальную форму (СДНФ) представления ФАЛ, в противном случае, используют совершенную конъюнктивную нормальную форму (СКНФ). Правило составления записи структурной формулы в виде СДНФ заключается в том, что для каждой строки таблицы истинности, в которой значение функции равно «1», записывается минтерм - конъюнкция (логическое произведение) всех входных переменных, а затем производится логическое сложение минтермов. Если значение какой-либо входной переменной, например  , в строке таблицы истинности равно нулю, то такая переменная записывается в минтерме в инверсном виде, т.е. , если равно единице – в прямом, т.е. .Правило составления записи структурной формулы в виде СКНФ заключается в том, что для каждой строки таблицы истинности, в которой значение функции равно 0, записывается макстерм - дизъюнкция (логическая сумма) всех входных переменных, после чего производится логическое умножение макстермов. При этом, если значение какой-либо входной переменной в строке таблицы истинности равно «1», то такая переменная записывается в макстерме в инверсном виде, если равно «0» – в прямом.. Минимизация ФАЛ заключается в нахождении минимальных нормальных форм ее записи (МДНФ или МКНФ), имеющих минимальное число вхождений входных переменных и минимальное число термов в функции. Напомним некоторые определения, которые полезно знать при рассмотрении различных методов минимизации применительно к записи ФАЛ в МДНФ. конъюнкции (логические произведения), входящие в СДНФ называются минтермами; число переменных (с инверсией или без), входящих в минтерм, называется его рангом. Например, конъюнкция  имеет второй ранг,  - четвертый;два минтерма, отличающихся только одной переменной называются соседними; ДНФ функции называется тупиковой (ТДНФ), если она не содержит избыточных переменных, таких, которые можно изъять без нарушения эквивалентности исходной функции; минимальной ДНФ (МДНФ) называется ТДНФ, содержащая наименьшее число переменных в минтермах и наименьшее число минтермов по сравнению с другими эквивалентными тупиковыми формами. При минимизации ФАЛ следует применять основные законы булевой алгебры, которые приведены в прил 1. Наиболее эффективными и поэтому часто используемыми при минимизации являются закон склеивания (прил. 1.15) и закон поглощения (прил 1.13). Более удобным методом минимизации ФАЛ при числе переменных  является метод карт Карно (диаграмм Вейча). Карта Карно представляет собой прямоугольник, разбитый на клетки, число которых для функции  переменных равно  , т.е. общему числу наборов значений функции (числу строк таблицы истинности), причем каждая клетка карты отличается от любой соседней, только одной инверсией одной из переменных. Например, для функции трех переменных число клеток в карте Карно равно  . Таким образом, каждой клетке карты соответствует один единственный набор значений переменных, представляющих собой координаты, на пересечении которых находится данная клетка.Карта Карно заполняется следующим образом: в каждой клетке проставляется значение функции, которое она принимает на наборе значений переменных, являющихся ее координатами. Так, при представлении функции в СДНФ в каждой клетке, координаты которой соответствуют минтерму, для которого функция принимает единичное значение, указывается значение «1», значение «0» при этом на картах обычно не отражается. При представлении ФАЛ в СКНФ в каждой клетке, координаты которой соответствуют макстерму (дизъюнкции), для которого функция принимает нулевое значение, указывается значение «0», значение «1», при этом на картах обычно не отражается. Так, для клетки, содержащей нулевое значение функции при значениях координат, указанных выше, макстерм будет иметь следующий вид:  .Минимизация ФАЛ заключается в объединении соседних клеток (при этом клетки, лежащие на границах карты, также являются соседними по отношению друг к другу), содержащих единичные (для получения МДНФ) или нулевые (для получения МКНФ) значения, в замкнутые области. Каждая область должна представлять собой прямоугольник с числом клеток  . Области могут пересекаться, и одни и те же клетки могут входить в разные области. Это позволяет исключить одну переменную при объединении двух клеток, или две переменные при объединении четырех соседних клеток, или три переменные при объединении восьми клеток карты Карно. При охвате клеток замкнутыми областями следует стремиться к минимальному числу областей, каждая из которых содержала бы возможно большее число клеток.Цифровые значения координат клеток карты Карно можно заменить также переменными, которые при данных значениях координат принимают прямое или инверсное значение. На рис. 2 даны варианты представления карты Карно для функции . |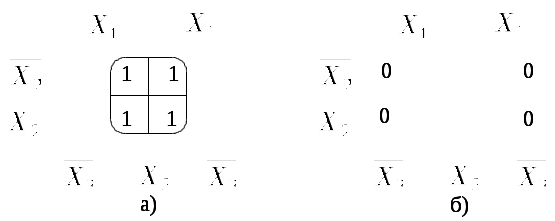
