Кр. Задание_на_кр. Структурный синтез дискретных автоматов
 Скачать 0.92 Mb.
|
|
Рисунок 2. Варианты представления карты Карно для функции  :а) для случая записи в СДНФ; б) для случая записи в СКНФНа рис. 2, а показана карта Карно для минимизации функции, представленной в СДНФ. В этом случае МДНФ может быть представлена в виде логической суммы минтермов, количество которых соответствует числу замкнутых областей. На рис. 2,б показана карта Карно для минимизации функции, представленной в СКНФ. В этом случае МКНФ может быть представлена в виде логического произведения макстермов, количество которых соответствует числу замкнутых областей. Для записи полученных в результате минимизации ФАЛ в базисах И-НЕ или ИЛИ-НЕ используют закон де Моргана (закон дуальности), согласно которому инверсия дизъюнкций  переменных равна конъюнкции инверсий этих переменных и, наоборот, инверсия конъюнкции переменных равна дизъюнкции инверсий этих переменных.В соответствии с законом де Моргана мы можем представить данную функцию в различных базисах. Для представления функции в базисе И-НЕ необходимо произвести двойную инверсию над всей функцией и, используя теорему де Моргана преобразовать инверсию дизъюнкций в конъюнкцию инверсий. Для представления функции в базисе ИЛИ-НЕ необходимо произвести двойную инверсию над каждой конъюнкцией, а также двойную инверсию над всей функцией и, используя закон де Моргана преобразовать инверсию конъюнкций в дизъюнкцию инверсий Двойное инвертирование ФАЛ не изменяет функцию, но позволяет исключить одну логическую операцию ИЛИ путем замены ее на две операции ИЛИ-НЕ. Для технической реализации ФАЛ используется количество логических элементов типа И-НЕ или ИЛИ-НЕ, равное числу инверсий в ее алгебраическом выражении. Так как любой из этих логических элементов должен иметь по определению число входов не менее двух, то при наличии инверсии только одной переменной, эта переменная подается на оба входа логического элемента И-НЕ или ИЛИ-НЕ в зависимости от выбранного базиса. ЗАДАЧА 2 Провести синтез автомата Мили, функционирование которого описывается заданными таблицами переходов и выходов. Изобразить граф синтезируемого автомата. Задавая произвольную двоичную последовательность (входное слово), определить соответствующую двоичную выходную последовательность (выходное слово) автомата. Построить структурную схему синтезированного автомата в базисе И, ИЛИ, НЕ. Варианты таблиц переходов определяются следующим образом: по последней цифре шифра из табл. 3 определяется последовательность восьми состояний (из четырех заданных А0, А1, А2, А3). Эта последовательность построчно слева направо и сверху вниз заносится в таблицу переходов, состоящую из двух строк, верхняя из которых определяет последующие состояния автомата под воздействием входного сигнала  , а нижняя -  .Таблица 3 Варианты таблиц переходов
Представить число из трех последних цифр шифра в двоичной системе счисления, добавив при необходимости слева нули до восьми разрядов или убрав (также слева) лишние, оставив восемь младших разрядов. Эта двоичная последовательность построчно слева направо и сверху вниз заносится в таблицу выходов, первая строка которой будет определять выходные сигналы автомата при воздействии входного сигнала , а вторая - .Заполняем соответствующие таблицы, как это показано на рис. 5.
Рисунок 5. Пример заполнения таблиц переходов и выходов МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАЧИ 2 Синтез последовательностных устройств Известно, что для синтеза комбинационных схем требуется набор логических элементов, реализующих некоторую полную систему логических функций (базис). Особенность последовательностных схем состоит в том, что они обладают памятью, для реализации которой требуются дополнительные элементы. В качестве таких элементов используются триггеры. Опишем структуру синтезируемого автомата Мили, относящегося к одной из разновидностей последовательностных схем. Автомат состоит из набора  элементарных автоматов (триггеров  ), комбинация состояний которых в каждый момент времени определяет внутреннее состояние в целом всего автомата. Под воздействием входных сигналов автомат должен переходить из одного состояния в другое. Для изменения состояния автомата необходимо переключить один или несколько триггеров, определяющих состояние автомата. Переключение триггеров осуществляется подачей сигналов  на соответствующие входы триггера. Так как новое состояние автомата определяется тем, каково было его прежнее состояние и каков набор входных сигналов, то и сигналы являются функциями выходных сигналов триггеров ( ) и входных сигналов автомата ( ).Для формирования сигналов управления триггерами используется комбинационное устройство. Структура этого устройства определяет функцию переходов автомата. Функция выходов реализуется другим комбинационным устройством, формирующим выходные сигналы автомата ( ). В автомате Мили выходные сигналы являются функциями его входных сигналов ( ) и выходных сигналов триггеров ( ), в отличие от автомата Мура, в котором выходные сигналы являются функциями лишь выходных сигналов триггеров.Функции переходов и выходов автомата могут быть заданы в форме таблиц переходов и выходов или с помощью графов. В столбцах таблиц (рис. 5) указаны состояния автомата, а в строках - входные сигналы. На пересечении столбца и строки в таблице переходов указано новое состояние, в которое переходит автомат, а в таблице выходов - выходной сигнал. Граф же состоит из узлов, отождествляемых с отдельными состояниями автомата. Связи между узлами показывают переходы автомата из одного состояния в другое под воздействием входных сигналов. На каждой связи сверху указывается входной сигнал, вызывающий данный переход, и сигнал, формируемый на выходе автомата до перехода его в новое состояние. Таким образом, для синтеза автомата необходимо выполнить следующее: определить какая комбинация состояний триггеров будет соответствовать каждому из внутренних состояний автомата, т.е. провести кодирование внутренних состояний автомата; синтезировать комбинационное устройство формирования сигналов управления триггерами , используя таблицу переходов;синтезировать комбинационное устройство, формирующее выходные сигналы автомата  , используя таблицу выходов.Затем каждой комбинации состояний триггеров нужно поставить в соответствие определенное состояние автомата. Кодирование состояний автомата может производиться различными способами. кодирования состояний автомата приведен в табл. 4. Таблица 4 Кодирование состояний автомата
Далее заполняем табл. 5 функционирования автомата Таблица 5 Таблица функционирования автомата Мили
Рассмотрим подробнее заполнение таблицы функционирования автомата Мили. В первых трех ее столбцах записываются все возможные сочетания кодов входного сигнала и состояния автомата. Для заданного входного сигнала и состояния автомата по графу находится значение выходного сигнала, которое записывается в последнем столбце таблицы, и следующее состояние автомата, в которое он переходит. Код этого состояния заносится в четвертый и пятый столбцы таблицы. Столбцы с 6 по 9 отведены для записи сигналов управления триггерами. Управление триггерами осуществляется подачей сигналов на входы очистки (вход  ) и установки (вход  ). Эти сигналы для каждого триггера определяются сравнением их состояний в момент времени  -  и в последующий момент времени  -  . Например, в первой строке табл.5  ,  . Это означает, что второй триггер переводится из состояния «0» в состояние «1».Для этого должен быть подан сигнал «1» на вход  и «0» на вход  . Во второй строке табл.5  , а  , следовательно, для перевода этого триггера из состояния «1» в состояние «0» необходимо подать сигнал «0» на вход  и «1» на вход  .В тех случаях, когда предыдущее и последующее состояния триггера совпадают, (триггер хранит предыдущее состояние), то на оба входа (очистки и установки) можно подать сигнал «0» ( ,  ), или на определенный вход триггера может подаваться сигнал подтверждения состояния триггера  , (установка «1») или ,  (очистка или установка «0»).В подобных случаях, когда логический уровень сигнала управления безразличен («0» или «1»), соответствующие клетки табл.5 остаются пустыми или в них заносится символ *. Для построения комбинационного устройства, формирующего сигналы управления триггерами (  ), необходимо найти их минимальные формы, используя метод минимизирующих карт (рис. 7).Для построения комбинационного устройства, формирующего выходной сигнал 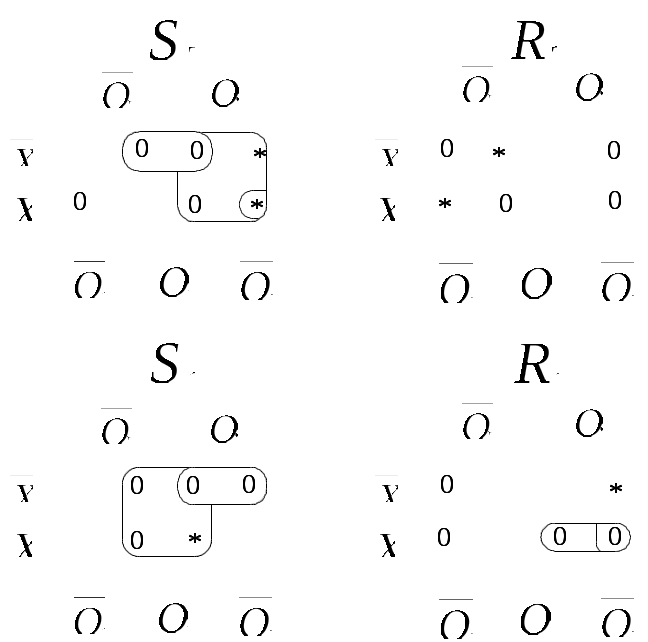 , находят его минимальную форму, используя метод минимизирующих карт. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
