Сущность задачного подхода. 5_Сущность задачного подхода. Сущность задачного подхода к преподаванию физики
 Скачать 72.58 Kb. Скачать 72.58 Kb.
|
|
Сущность задачного подхода к преподаванию физики С точки зрения теории проблемного обучения учебный процесс можно рассматривать как последовательную постановку и решение ряда задач. Структура и дидактическое назначение их могут быть различными, но, если брать понятие задачи в широком смысле слова, то в качестве объектов, служащих основанием для них, могут выступать такие дидактические единицы, как рассказ, практическая и лабораторная работа, кинофильм, собственно предметная задача. Рассмотрение задач предполагает в первую очередь определение их функций, которые вытекают из общих целей обучения и воспитания учащихся, зависящих в свою очередь от социального заказа школе. Общество требует, в частности, от школы подготовки высокообразованной личности, не только обладающей всесторонними знаниями, но личности думающей, умеющей применять имеющиеся знания в разнообразных, в том числе нешаблонных ситуациях. Один из путей решения этой проблемы состоит в задачной организации учебного процесса, что предполагает широкую трактовку самого понятия задачи, обучение учащихся общим подходам к процессу постановки и решения задач. Ниже речь пойдёт только о собственно задачах, но основные положения, высказанные при этом, могут и должны быть, в связи со сказанным, применимы и к другим структурным единицам дидактики. Следует заметить, что в методической литературе назначение учебных задач рассматривается чаще всего как средство применения, закрепления полученных знаний, их контроля, самостоятельного приобретения знаний (последние в гораздо меньшей степени). Однако роль учебных задач существенно шире. Только путём включения задач в учебный процесс можно сформировать у учащихся те или иные подходы к учебному материалу, отработать мыслительные операции, вывести их на высший уровень сформированноcти знаний, связанный с умением применять знания в новых, нестандартных ситуациях. Адекватность процесса мышления процессу решения задач говорит о дидактической незаменимости задач другими средствами. При этом задачи должны ни столько способствовать закреплению знаний, тренировке в применении изученных законов, сколько формировать сам исследовательский стиль умственной деятельности, метод подхода к изучаемым явлениям. А раз основным ориентиром в обучении является стиль мышления ученика, развитие его творческих способностей, объектом анализа в первую очередь должно являться не решение отдельных конкретных задач по тому или иному предмету, а общий метод их решения, процесс постановки и решения задач вообще. Для этого необходима система задач, нацеленная на формирование у учащихся методов поисковой деятельности, самостоятельности мышления. Эта деятельность с позиции задачного подхода к учебному процессу связывается, в первую очередь, с необходимостью преобразования информации, определяемой в качестве учебной. В результате преобразования происходит осмысление информации и, соответственно, принятие или непринятие её субъектом как ценности. С этой точки зрения сам процесс преобразования представляет особый интерес с позиции дидактики, поскольку является действенным способом формирования определённого эмоционально-чувственного отношения учащихся к учебному материалу. Задачи являются информационными системами, к которым в наиболее явной форме предъявляются требования в их преобразовании. Само решение задачи есть ни что иное, как система последовательных преобразований данных и вопроса задачи. Это полностью относится и к учебным физическим задачам. Покажем это на примере. Исходная задача Небольшое тело соскальзывает с наклонной плоскости, переходящей в «мёртвую петлю». Какой должна быть минимальная высота горки, чтобы тело сделало полный оборот? При анализе предложенного сюжета, задача разбивается на две относительно независимые задачи, решаемые последовательно друг за другом: Подзадача 1 Какую скорость должно иметь тело, движущееся по внутренней части обруча в верхней его части, чтобы не упасть? Подзадача 2 Небольшое тело соскальзывает с наклонной плоскости, переходящей в «мёртвую петлю». Какова должна быть высота горки, чтобы в верхней части петли тело имело скорость v? Далее, по мере решения каждой из этих задач, идёт дальнейшее преобразование их текстов в направлении выделения более мелких подзадач, соответственно, с переформулировкой текста основной задачи. Например, после определения способа решения первой задачи с помощью второго закона Ньютона, текст ее будет первоначально сформулирован следующим образом: Подзадача 3 Тело, движущееся по внутренней части окружности, проходит верхнюю точку со скоростью v. Какие силы действуют на него в системе отсчёта, связанной с Землёй? После ответа на поставленный вопрос и некоторых математических преобразований, текст задачи перестраивается следующим образом: Подзадача 4 Уравнение движения тела имеет вид: Какова скорость движения тела? Подобным же образом может быть разбита на более мелкие задачи и вторая подзадача. Приведённый пример показывает, что процесс решения и постановки задачи неразрывно связаны друг с другом, поэтому не следует разделять их в учебном процессе. Напротив, ученика следует учить способам постановки и способам преобразования текстов задач по мере их решения. К тому же, в жизни человеку редко приходится сталкиваться с готовыми, уже сформулированными задачами, но необходимость их ставить велика. Это также говорит о том, что процесс работы над задачей следует начинать с этапа её постановки. При этом могут реализоваться две принципиально разные возможности в подходе к постановке задачи: задачу ставит учитель и задачу ставит ученик. В процессе самостоятельного составления задачи ученик частично выполняет работу, характерную для учителя. При этом его функции за счёт выполнения конструктивной деятельности расширяются. Ученик становится не только объектом, на который направлен педагогический процесс, но и активным его участником. Необходимость рассматривать задачу с этапа её постановки обусловливается не только адекватностью этой операции реальным жизненным ситуациям, но и внутренней природой самого процесса решения задачи. Часто формулировка задачной ситуации и вопроса к ней уже определяют направление в решении и способы решения задачи. Именно таким образом, чётко, конкретно и ясно сформулировано большинство задач в школьных сборниках задач. Примером может служить следующая задача. «На наклонной плоскости длиной 5 м и высотой 3м находится груз массой 50 кг. Какую силу, направленную вдоль плоскости, надо приложить, чтобы этот груз втягивать вверх с ускорением 1 м/с2? Коэффициент трения скольжения груза о поверхность плоскости равен 0,2». Из условия задачи совершенно ясно, что она решается с помощью второго закона Ньютона, поскольку именно этот закон определяет соотношение между силами, действующими на тело и ускорением его движения. Алгоритмическое предписание по решению динамических задач достаточно хорошо известно и при использовании его, нахождение ответа к поставленной задаче не вызывает труда. И наоборот, в психологических исследованиях показано, что часто сформулированный вопрос не позволяет решить задачу. Вопрос может подталкивать мысль не в том, и даже в противоположном направлении, поэтому в сложных реальных задачах часто по ходу анализа перестраивается не только содержание задачи, но и само требование. Более того, суть большинства творческих задач заключается в необходимости отказаться от уже поставленного в тексте задачи требования и построить новое, по своему смыслу совершенно или частично не совпадающее с предыдущим. И именно характер вопроса к задаче, соответствие его дальнейшему ходу решения, а так же число переформулировок текста задачи определяют степень её трудности. Процесс решения нередко предполагает тупиковые ситуации, вызванные неверно сформулированными вопросами или неверно заданными условиями. Отсюда следует, что важно показать ученику способы действий при встрече с такими ситуациями. В связи с этим, среди учебных задач могут быть выделены специальные задачи, посвящённые анализу тупиковых ситуаций, неверных условий и т. п. Хорошей иллюстрацией к сказанному является следующая задача. Исходная задача: С какой минимальной скоростью следует бросить камень, чтобы перебросить дом высотой H и длиной L? На первый взгляд, эта задача представляется недоопределённой и усилия решающего нередко затрачиваются именно на доопределение задачи, т. е. на поиск точки, из которой производится бросок и угла, под которым он производится. При этом решающий неявно переформулирует задачу и сводит её к такой: Какую скорость следует сообщить камню, брошенному под углом из точки с координатами (x0, y0), чтобы перебросить дом высотой H и длиной L? Недостаточное количество данных для этой задачи часто не позволяет решающему подвинуться дальше в ее решении, т. е. осуществить следующие переформулировки. Неверное направление анализа, вызванное специфической формулировкой задачи приводит к психологическому барьеру, поставленному самим решающим. В подобной ситуации следует научить учащихся отказываться от созданной ими формулировки и пытаться провести анализ основной задачи в другом направлении и, соответственно, по-иному сформулировать задачу. Предлагаемая задача, например, может быть сформулирована вновь так: Какой должна быть траектория движения камня, чтобы на высоте H он при минимальной скорости перелетел крышу длины L? Такая формулировка как дает плодотворную идею решения задачи, так и позволяет на качественном уровне доопределить предыдущую неверно сформулированную задачу. Среди множества задач можно выделить группу таких задач, в которых вопрос хотя и сформулирован, но для решающего остаётся неясным, что следует в задаче искать, что же в ней в действительности является неизвестным. В таких задачах основная трудность состоит в первоначальной переформулировке поставленного вопроса. Часто трудность такого рода состоит в том, что вопрос к задаче сформулирован не в терминах того предмета, к которому относится сам сюжет задачи. Например, задача может быть физической, а вопрос к ней сформулирован на житейском языке. Перевод вопроса на язык задачи означает переформулировку ее текста и снимает первый и основной психологический барьер его неясности. Правильная переформулировка определяет уже и направление решения задачи. Задачи такого вида обычно относятся к олимпиадным. Примером может служить следующая задача: Формулировка задачи в терминах житейского языка: Почему сосиски лопаются при варке обычно вдоль, а не поперек? Формулировка задачи в физических терминах: Как отличаются силы, приходящиеся на единицу длины поперек и вдоль сосиски при возрастании давления внутри нее на величину p? Встречаются случаи, когда вопрос к задаче сформулирован вроде бы и ясно, но, в то же время, совершенно не понятно, что же в задаче следует искать, т. е. в рамках какой теории решать задачу. Пример: С какой скоростью нужно бежать по воде, чтобы не утонуть? Как было показано, неверно поставленный вопрос может служить своеобразным психологическим барьером при решении задачи. В качестве барьеров могут выступать и данные задачи - недостающие, либо лишние, и опыт прошлого решения задачи, поэтому одно из требований к тексту задачи должно заключаться в большей или меньшей степени их неопределённости. Это приблизит учебные задачи по содержанию к конструкторским задачам, которые являются задачами - проблемами в полном смысле этого слова. При обозначенном выше подходе, учащимся могут предлагаться недоопределённые задачи, точнее задаваться модели физических процессов. Деятельность ученика при этом должна заключаться в: 1) формальном описании с помощью математических формул заданного процесса; 2) задании величин и формулировке сюжета задачи; 3) постановке вопроса. Рассмотрим в качестве примера процесс движения тела по наклонной плоскости при наличии трения между соприкасающимися поверхностями. Как видно из приведённой формулировки, в качестве объекта анализа предлагается не задача, построенная на основе конкретного сюжета и имеющая текст и вопрос, а физический процесс. Тем не менее, формальное описание этого процесса может идти в соответствии с тем же алгоритмическим предписанием, что и решение любой задачи на движение тела по наклонной плоскости. Например, если в качестве такого предписания будет выбрано алгоритмическое предписание по решению задач на основе второго закона Ньютона, то после - выбора системы отсчёта, - выполнения чертежа с нанесением на него динамических и кинематических характеристик движения, - записи уравнения второго закона Ньютона в векторной форме и в проекциях на оси координат, - решения полученных скалярных уравнений, мы будем иметь выражение вида: При необходимости, это уравнение можно переписать, введя кинематические характеристики: Полученное уравнение описывает процесс движения тела по наклонной плоскости, если на это тело не действует сила тяги со стороны другого тела. Анализируя рассматриваемый процесс и полученное уравнение, можно сформулировать множество различных задач, которые решаются одинаковым образом, так же, как формально описывался процесс движения тела по наклонной плоскости безотносительно какого- либо вопроса. Например, это могут быть задачи такого содержания: Для случая а = 0 : Определить коэффициент трения скольжения дерева по дереву, если небольшой брусок, положенный на деревянную линейку длины L см, начинает соскальзывать с неё при поднятии одного из концов линейки на высоту h см над горизонтальной поверхностью? Для случая а >0: Определить значение силы тяги, которую следует приложить к телу, чтобы равномерно поднимать его по наклонной плоскости, расположенной под углом к горизонту. Для случая Определить ускорение движения тела по наклонной плоскости, расположенной под углом к горизонту. Определить перемещение, которое совершает тело, движущееся по наклонной плоскости, расположенной под углом к горизонту, за время t. Определить, за какое время тело соскользнёт с наклонной плоскости длины L, если плоскость расположена под углом к горизонту. Существенно, что данный подход может быть использован как при формулировке теоретических задач, так и заданий экспериментального характера. О необходимости меньшей определённости в текстах задач при их постановке говорил в 1970 г. на Международном конгрессе по вопросам подготовки преподавателей физики для средней школы академик П.Л. Капица. Он отмечал, что именно при таком подходе к постановке задач можно воспитывать самостоятельное творческое мышление учащихся. Всем преподавателям физики, вероятно, известны знаменитые задачи Капицы для студентов, задачи недоопределённые, часто не имеющие точного решения. Именно аналогичные, только менее трудные задачи предлагает П.Л. Капица давать для обсуждения и учащимся. Это задачи типа: Определить мощность мотора насоса, необходимого для поддержания струи, чтобы тушить пожар шестиэтажного дома. При решении таких задач ученик должен сам, на основании собственного жизненного опыта, подобрать необходимые ему данные, предварительно формально описав предложенное физическое явление. Возможны и специальные случаи, когда учащимся предлагают вполне определённые, но неправильно поставленные задачи. Но, разумеется, как отмечает Л.М. Фридман в книге «Как научиться решать задачи», что учитель при этом полностью понимает суть и назначение таких задач. Особое внимание должно быть обращено на постановку цели, которая преследуется при решении задач. Рассмотрим отдельные цели, возможные при решении школьных физических задач. Решение задач с целью формирования физических понятий Например, в разделе «кинематика» курса механики одними из основных являются понятия пути и перемещения. Учащиеся достаточно хорошо понимают разницу между ними, но, тем не менее, при решении некоторых задач путают их. Особенно это относится к случаю, когда тело движется вдоль одной прямой, но в какой-то момент времени меняет направление своего движения. Чтобы иметь полное представление о той или иной величине, надо знать не только ее особенные, но и отличительные черты. Для демонстрации отличия понятий пути и перемещения можно предложить учащимся следующую задачу: Тело, имеющее скорость 10 м/с, с некоторого момента начинает двигаться с ускорением Какой путь пройдёт это тело за первые 6 секунд, начиная с момента начала торможения? Обычно эта задача решается сразу по формуле: Чтобы навести решающего на мысль об ошибочности решения, можно предложить ему рассчитать путь, пройденный телом за 8 секунд, считая с момента начала замедленного движения. Ответ получается меньшим, чем в первом случае, что противоречит как здравому смыслу, так и определению пути. Ошибка в подходе к решению задачи связана с барьером прошлого опыта решения задач и кажущейся лёгкостью решения (имеется расчётная формула и все необходимые для подстановки в неё данные). Более детальный анализ сюжета задачи и методичное следование пунктам алгоритмического предписания по решению кинематических задач позволяют как найти искомый путь, так и выяснить, в чем состоит различие между понятиями пути и перемещения. Параллельно с этим обращается внимание на необходимость следования алгоритмическому предписанию по решению задач, даже несмотря на кажущуюся вначале их простоту. Решение задач с целью формирования представлений о границах применимости формул, законов В курсе кинематики средней школы изучается равнопеременное движение. Это движение описывается выражениями вида:  У учащихся часто складывается неверное представление об универсальном характере действия этих формул в случае неравномерного движения. В связи с этим возникают трудности в объяснении разных ответов при использовании непротиворечивых формул при решении следующей задачи: Троллейбус, имевший скорость 10 м/с, начал тормозить. При каком ускорении он пройдёт до полной остановки 8 м за 2 с? Решение:  Суть ответа сводится к тому, что если считать движение равнозамедленным, то одно из данных задачи является лишним и неверным. В случае такого движения, подобного соотношения данных быть не может. Но возможен и такой вариант, когда все данные являются верными, но тогда движение должно быть неравнозамедленным и ни одна из использованных формул для его описания применена быть не может. Анализ подобной задачи позволит лучше, чем где-либо показать границы применимости используемых при решении задач формул. Решение задач с целью демонстрации рациональных и нерациональных способов решения, а так же необходимости использования предписаний алгоритмического типа Гораздо большую пользу принесёт учащимся решение одной задачи несколькими способами, нежели решение большого количества задач одним способом. При этом среди разных способов можно выделить способы как рациональные, так и нерациональные. Часто рациональные способы не используются учащимися в силу тех или иных особенностей мышления, привычки и т.д. Перед учащимися возникают своеобразные психологические барьеры, перешагнув через которые они дальше без особого труда могут решить предлагаемую задачу способом более рациональным и легким, нежели способом стандартным или кажущимся лёгким на первый взгляд. Приведём пример задачи: Из гондолы воздушного шара, поднимающегося вертикально вверх с постоянной скоростью 10 м/с, выпал предмет, который упал на Землю через 5 с. На какой высоте находился шар в тот момент, когда предмет коснулся Земли? Очень часто такую задачу решают поэтапно: 1. Находят время движения выпавшего предмета вверх: 2. Находят время падения предмета до того места, откуда он выпал из гондолы шара: t2 = t1 = 1с и скорость в этой точке. v = 10 м/с и направлена вертикально вниз. 3. Находят перемещение предмета за оставшиеся 3 с, т.е. высоту, на которой находился шар в момент отделения от него предмета h1=75 м. 4. Находят перемещение шара за 5с. 5. Находят общую высоту как H = h1+h2; H = 125 м. Но эта же задача может быть решена с помощью координатного метода. Записываются уравнения движения шара и тела в системе отсчёта, связанного с Землёй:  y y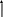 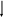 y0 y0  ; ; v0 g  0 По условию задачи: 0 По условию задачи: В итоге оказалась невостребованной скорость шара. Уже отсюда вытекает, что хотя первый способ и кажется физически более понятным и простым, на самом деле он становится неприемлемым, как только из условия задачи будет исключена скорость шара. Приведённые решения позволяют показать преимущества общего подхода к решению кинематических задач. Но задача имеет и более рациональное решение. Если связать систему отсчёта с движущимся шаром и ось у направить вертикально вниз, то уравнение движения тела запишется: 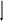 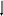 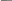 y g y g Такое решение редко приводится учащимися в силу того, что они «привыкли» связывать систему отсчёта с Землёй, каким-то неподвижным телом. Решение задач, направленное на демонстрацию ошибочности использования наиболее очевидных формул, законов Задача. Поезд первую половину пути шёл со скоростью 30 км/ч, а вторую половину пути - со скоростью 50 км/ч. Какова средняя скорость движения поезда на всем пути? Типичный ответ – 40 км/ч, который сразу дают ученики, связан с внешним, хотя и очень отдалённым сходством предлагаемой задачи с задачами на отыскание среднего арифметического. Эта кажущаяся очевидность и заставляет учеников «забыть» хорошо известную им определительную формулу для вычисления средней скорости: Чтобы навести учащихся на мысль об ошибочности их ответа целесообразно сразу же привести задачу с теми же данными, но слегка изменённым сюжетом: Поезд первую половину времени шёл со скоростью 30 км/ч, а вторую половину времени - со скоростью 50 км/ч. Какова средняя скорость поезда на всем пути движения? И только после того, как учащиеся задумаются над вопросом – в чем разница между задачами, можно их решить, акцентировав внимание на совершенно одинаковом подходе к решению и необходимости знания всего лишь одной определительной формулы для решения разных задач на нахождение средней скорости. Особо ещё раз следует отметить, что для достижения цели, задачи должны предлагаться с очень похожим сюжетом, с одинаковыми числовыми значениями и обязательно в паре - одна за другой. Решение задач для закрепления теоретических выводов Известно затруднение в решении ряда задач на колебательные системы, вызванное некорректностью, либо поспешностью выяснения физического смысла коэффициента пропорциональности «k» в дифференциальном уравнении, описывающем гармонические механические колебания: Это задачи, аналогичные такой: В жидкости плавает ареометр. Его выводят из положения равновесия путём лёгкого погружения в жидкость, после чего отпускают. Найти период колебаний ареометра. Сопротивлением движению пренебречь. При изучении темы «Механические колебания» один из акцентов должен быть сделан на том, что поскольку формула При этом последовательность действий по решению задач данного вида будет такой: Ставится вопрос: является ли рассматриваемое движение гармоническими колебаниями, т.е. пропорциональна ли сила, выводящая тело из положения равновесия, смещению и направлена ли эта сила к положению равновесия? Если при анализе выяснится, что результирующая сила, действующая на тело, не пропорциональна смещению, то формула Если же, наоборот, сила оказывается пропорциональной смещению, то период колебаний будет находиться по этой формуле. Для нахождения периода достаточно будет подставить в имеющуюся формулу значение коэффициента пропорциональности между силой и смещением, которое получается при количественном анализе задачи. Таким образом, сложная для учащихся задача может стать обычной стандартной и использоваться в данном случае как упражнение, направленное на закрепление и отработку полученного в теории знания. Существенное место в деятельности учителя по конструированию учебно-воспитательного процесса (в том числе и в рамках задачного подхода) отводится отбору образовательного, в частности, фактологического материала для урока. Не вдаваясь в суть и состояние проблемы, отметим лишь, что следует показывать существование и жизненность объективных закономерностей развития общества и определяемых ими закономерностей развития производства, орудий труда, перспективы их роста. Учителю надо находить возможности для изучения таких материалов во время учебного процесса. Особое внимание при этом должно быть обращено на способы формирования у учащихся глубоких и прочных знаний материалов, составляющих сюжет задачи и используемых при ее постановке в качестве вспомогательных. Один из путей включения школьников в активную деятельность связан с самостоятельным поиском ими числового материала в справочниках или указанной учителем литературе. Можно составлять задачи на материале местного производства. При этом в разных школах целесообразно использовать краеведческие задачи, наиболее близкие учащимся. На основе этих задач и общих принципов ученики легко смогут провести экстраполяцию изученных закономерностей в другие области народного хозяйства. Как было отмечено выше, в процесс конструирования учебных физических задач могут быть включены учащиеся. Процесс самостоятельного поиска злободневного материала и конструирование на его основе текстов задач должны иметь большие воспитательные и развивающие потенции. Чтобы работа по отбору фактологического материала носила развивающий характер, необходимо направить ее на систематизацию этого материала. В курсе физики, само содержание учебного материала определяет один из важнейших принципов его отбора - в соответствии с основными направлениями развития производства. Объединение материала вокруг основных направлений развития производства вызывает необходимость в его первичном преобразовании, а, следовательно, уже на этом этапе отбора материала требует совершения тех или иных мыслительных операций. В соответствии с теорией поэтапного формирования умственных действий, задачи должны строиться учеником на разной ориентировочной основе. Соответственно, должны выделяться и разные виды предлагаемых учащимся заданий в зависимости от сложности преследуемых целей. Начинать обучение составлению задач следует с отработки простых операций. Ученику предлагается готовый сюжет задачи с поставленным вопросом, но не заданными или заданными не полностью фактическими и числовыми данными. От ученика требуется осуществить подбор данных, пользуясь указанной учителем литературой, материалами, полученными во время производственных экскурсий так, чтобы эти данные отражали тенденции развития отдельных направлений производства. На этом этапе учащимся предлагается найти лишь часть данных, заменить в условиях задач устаревшие данные новыми. Например, при изучении темы «Работа и энергия» решаются задачи на преобразование механической энергии в электрическую, осуществляемую, в частности, на гидроэлектростанциях. Энергетическое уравнение, описывающее подобные процессы, имеет вид: N t = mgh . На основе этого уравнения учащимся может быть предложена, например, такая задача: Мощность на валу гидротурбины N-й ГЭС составляет ..... МВт. Коэффициент использования энергии потока ....... %. Определить расход воды в секунду, если высота напора составляет ......... м. Кроме того, учащимся даётся задание конкретизировать условие задачи, взяв параметры современных ГЭС на страницах (указываются источники информации). Выполняя это задание, учащиеся должны прочитать цельный отрывок предложенного текста и сделать выборку необходимого материала. При этом они неизбежно будут выполнять простейшие операции по его преобразованию в соответствии с конкретными ориентирами и получать дополнительную информацию (имеются в виду данные о работающих и вводимых в строй электростанциях, основных тенденциях в их строительстве и т.п.). Для закрепления этой информации, с учащимися может быть проведён дополнительный разговор. Здесь же решается задача на преобразование внутренней энергии топлива в механическую энергию энергоблоков паровых турбин. Энергетическое уравнение, описывающее эти процессы имеет вид: N t = q m. Учащимся предлагается задача вида: Энергоблок паровой турбины мощностью N1 расходует на 1 кВт ч М1 кг условного топлива, а энергоблок мощностью N2 расходует на выработку 1 кВт ч - М2 кг условного топлива. Определить КПД турбины. Сколько топлива экономится за сутки на N-й ГРЭС по сравнению с М-й ГРЭС? Конкретные данные можно найти на страницах (так же указывается источник). Прочитав предложенный отрывок, учащиеся не только смогут подобрать необходимые данные и получить сведения о современных энергетических установках, но и узнать, что КПД растёт с увеличением единичных мощностей энергоблоков. После выполнения задачи, полученные сведения могут быть дополнительно обсуждены в беседе с учащимися. Примеров задач такого типа может быть приведено много. Уровень их сложности является минимальным, поскольку деятельность, связанная со вторым преобразованием, необходимым при конструировании текстов задач, для ученика пока снята, а для проведения первого преобразования, производимого при отборе информации, заданы конкретные ориентиры в виде явно выраженных требований найти ту или иную информацию. На этом уровне формируются начальные поисковые умения учащихся и производится первичное знакомство с фактическим и числовым материалом. К заданиям более высокого уровня сложности могут быть отнесены задания, при выполнении которых учащиеся вовлекаются в деятельность по самостоятельному первичному преобразованию информации. В отличие от заданий предыдущего уровня, конкретные указания о требованиях к отбираемому материалу заменяются ориентирами более общего характера, задающими направление в поисковой деятельности в виде системы целевых установок (показать пути роста промышленного и сельскохозяйственного производства, экономии природных богатств и т.д.). На этом этапе отрабатываются умения производить элементарные операции по преобразованию информации в соответствии с ориентирами обобщённого характера. Здесь учащимся могут предлагаться задачи, аналогичные следующей: Каково ежесуточное потребление топлива современными ТЭС, АЭС? За счёт чего достигается экономия топлива на современных ТЭС, АЭС? Каковы тенденции развития теплоэнергетики в нашей стране? Необходимые данные учащиеся могут найти в указанных учителем источниках. В отличие от задач первого типа, содержание этих задач является более неопределённым. В предлагаемых информационных сообщениях нет сведений, которые учащиеся могли бы сразу включить в текст задачи. Нет так же и прямых указаний на то, какие именно данные следует использовать для того, чтобы ответить на поставленный вопрос. Учащиеся предварительно должны решить задачу в общем виде, или, как было показано выше, описать математически предложенный физический процесс, а затем самостоятельно определить, какие данные следует искать в предложенных материалах. К этому же этапу относится деятельность по обучению учащихся осуществлению операции синтеза, которая заключается в конструировании текстов задач на основе предложенных физических явлений путём включения в них готовых информационных сообщений. Здесь же даются задания на постановку вопроса к предложенному задачному сюжету. Примером задачи такого вида может быть следующая: ТЭС мощностью P МВт потребляет в сутки Мкг топлива. Взять данные для давно введённых и новейших ТЭС. На основе их сравнения составить задачу так, чтобы вопрос отражал уровень и тенденцию развития страны в области теплоэнергетики. |
