технология электронных таблиц. Технология электронных таблиц контрольная работа. Табличный процессор Microsoft Office Excel
 Скачать 1.88 Mb. Скачать 1.88 Mb.
|
|
Построение полярных графиков и поверхностей Задание 2 Построить полярный график функции Порядок выполнения работы 1. Табулировать заданную функцию, пользуясьарифметическойпрогрессиейдляформированиязначенийаргументаиавтозаполнениемформулойсотносительнойадресацией – для вычисления значений заданной функции. 2. Выделить диапазон заполненных ячеек и построить плоский график (тип диаграммы – График) в декартовой системе координат. 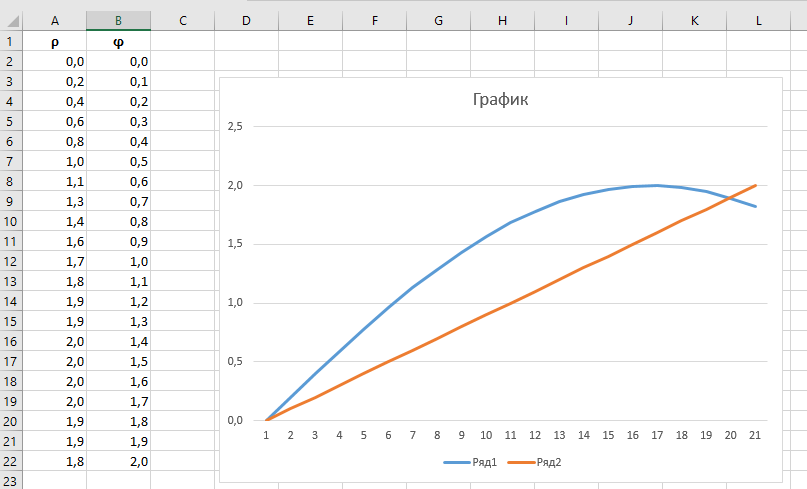 3. Для этих же данных построить полярный график (тип диаграммы – лепестковая). В полярных координатах положение точки на плоскости определяется расстоянием r этой точки от центра координат, который в этом случае называется полюсом, и углом поворота j [рад], между лучом r и полярной осью (в Excel – это вертикаль, проведенная из полюса вверх). Таким образом получается, что значения функции откладываются из центра координат в виде луча определенной длины, а аргумент, являющийся числом на оси Ох, преобразуется в угол поворота этого луча относительно полярной оси. 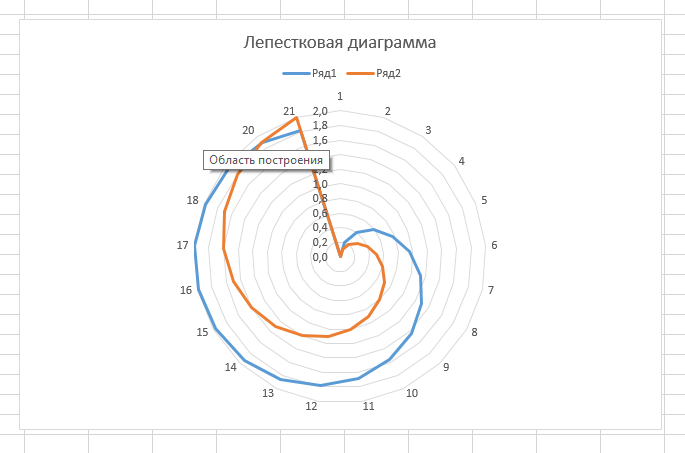 4. Сравнить полученные диаграммы. Чем отличается принцип построения этих типов графиков? Задание 3 Построить поверхность z = x2 – y2 при х, у Порядок выполнения работы 1. Наследующем листе построить поверхность или трехмерную диаграмму (предварительно преобразовать заданное выражение относительно z). 2. Табулировать заданную функцию следующим образом: в столбец А, начиная с ячейки А2, с помощью арифметической прогрессии ввести значения аргумента х; в строку 1, начиная с ячейки В1 с помощью арифметической прогрессии ввести значения аргумента у. 3. В ячейку В2 ввести формулу, соответствующую заданной функции, используя при этом смешанную адресацию: - для аргумента х – указать абсолютную ссылку на имя столбца, в котором хранятся его значения, т.е. на столбец А; - для аргумента у – указать абсолютную ссылку на номер строки, содержащей эти значения, т.е. на строку 1. Например, для поверхности z = x2 – y2 формула будет иметь вид: =$A2^2-B$1^2 Создать сетку значений для каждой пары аргументов х – у: с помощью маркера заполнения размножить формулу из ячейки В2 на весь диапазон. 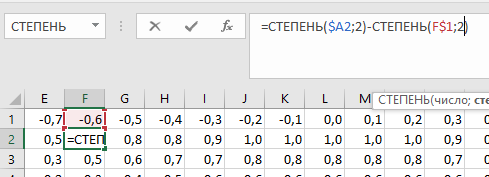 4. Выделить блок рабочего листа Excel, содержащий значения функции z и ее аргументов, и построить трехмерную диаграмму типа Поверхность. Ряды данных при этом должны находиться в столбцах. 5. Отформатировать диаграмму.  Задания для самостоятельного выполнения Построить указанные графики (поверхность и полярный) согласно вариантам (1 – 5). Для построения указанных в таблице типов диаграмм (столбцы «Тип диаграммы») использовать полученные случайным образом значения в заданных диапазонах (лабораторная работа 1).  Поверхность 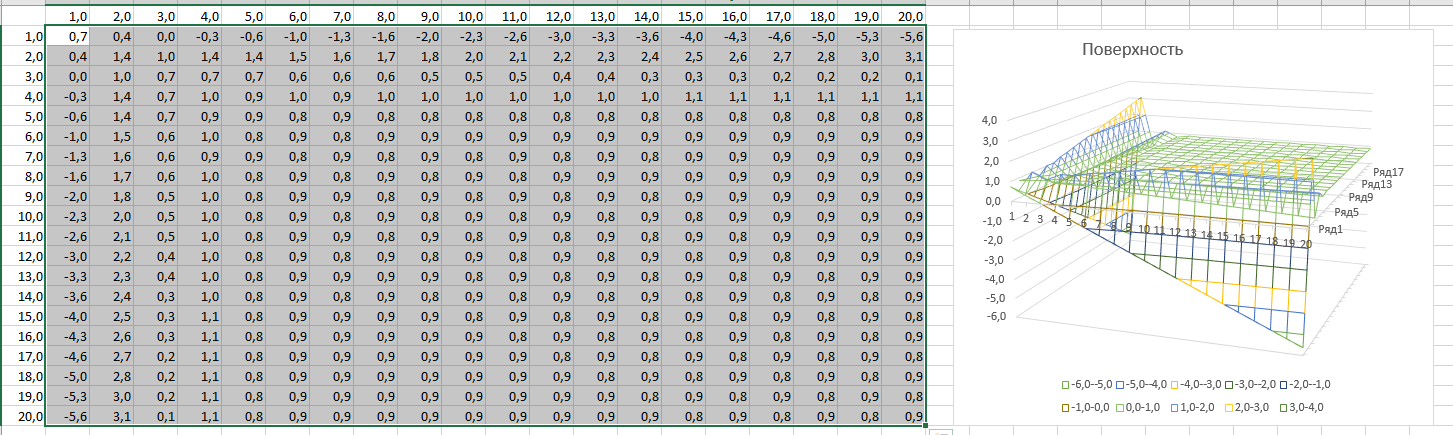 Полярный график 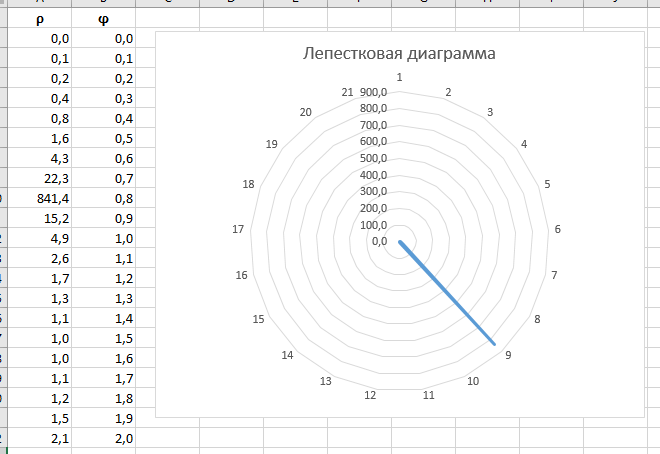 Диаграммы по случайным значениям, 5 вариант: 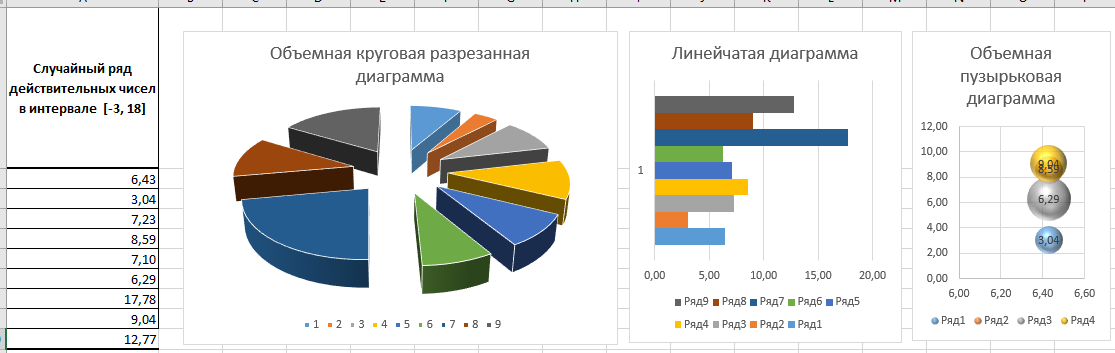 Лабораторная работа 3 ЛОГИЧЕСКИЕ ФУНКЦИИ В EXCEL Цели работы: 1. Изучить логические функции MS Excel. 2. Научиться использовать логические функции для построения таблиц истинности. 3. Изучить описание функций с условиями и построение их графиков. 4. Создать таблицу вычисления арифметических выражений в позиционных системах счисления. 5. Изучить применение функций ЕСЛИ, СЧЁТЕСЛИ для обработки табличной информации. Задание 1 Построить таблицу истинности логического выражения (ИСТИНА или ЛОЖЬ). Порядок выполнения работы 1. Дать рабочему листу название «Лог. выражение». 2. Заполнить ячейки рабочего листа значениями логических переменных X, Y, Z. 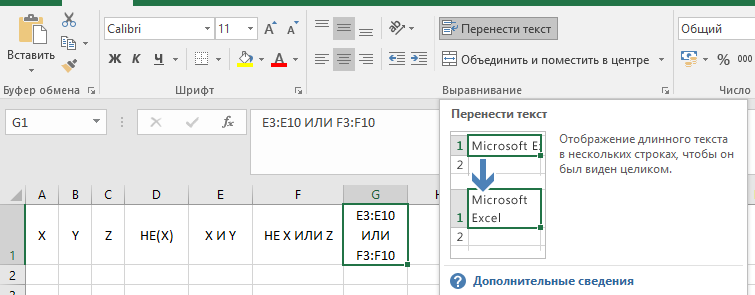 3. Вычислить значения элементарных логических операций И(), ИЛИ(), НЕ() (столбцы D – G). 4. В последнем столбце записать логическое выражение X ˆ Yˇ (¬X ˇ Z) (значения двух последних столбцов должны совпадать). 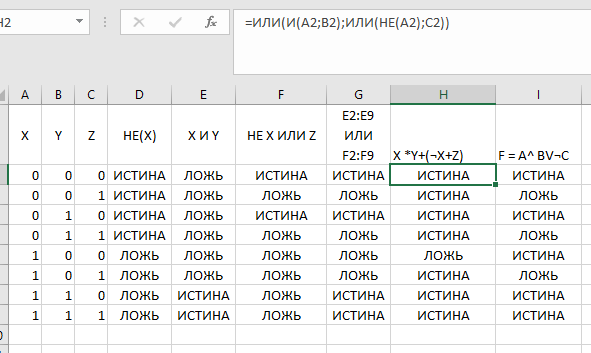 5. Отформатировать ячейки таблицы (использовать Переносить по словам). Задание 2 Табулировать функцию 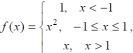 построить график. построить график.Порядок выполнения работы 1. Дать рабочему листу название «Лог. функция». 2. Используя арифметическую прогрессию, сформировать ряд значений аргумента (столбец А). 3. В строке формул для столбца B задать значение логической функции (использовать авто заполнение с относительной адресацией). 4. Выделить диапазон заполненных ячеек и построить плоский график в декартовой системе координат. 5. Отформатировать диаграмму, отслеживая правильность значений по оси Ох 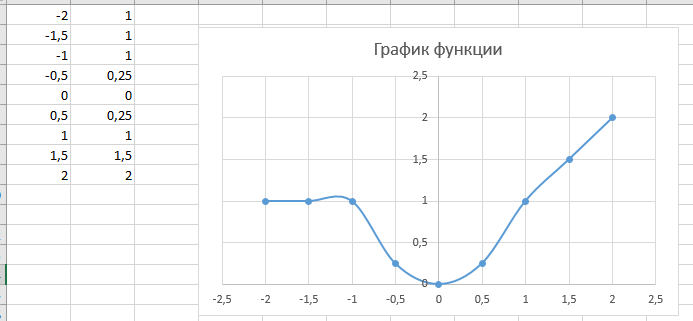 Задание 3 Создать таблицу значений арифметических действий в восьмеричной системе счисления (использовать функции перевода чисел категории Инженерные). Порядок выполнения работы 1. Дать рабочему листу название «Восьмеричная». 2. Заполнить таблицу сложения восьмеричных чисел согласно образцу. 3. Заполняем значения в таблицу через функцию =Дес.В.Восьм(число).В ячейку сложения чисел В3 вводим формулу подсчета суммы восьмеричных чисел =ДЕС.В.ВОСЬМ(ВОСЬМ.В.ДЕС(B$2)+ВОСЬМ.В.ДЕС($A3)) и копируем формулу на весь диапазон значений. 4. Командой «Главная – Шрифт – Заливка» выделяем ячейки с «неверными» десятичными вычислениями. 5. В ячейку В10 таблицы вычитания вводим формулу =ДЕС.В.ВОСЬМ(ВОСЬМ.В.ДЕС(B$9)-ВОСЬМ.В.ДЕС($A10)) и с помощью маркера автозаполнения копируем формулу на весь диапазон значений. 6. В ячейку В17 таблицы вычитания вводим формулу =ДЕС.В.ВОСЬМ(ВОСЬМ.В.ДЕС(B$16)* ВОСЬМ.В.ДЕС($A17)) и с помощью маркера автозаполнения копируем формулу на весь диапазон значений. 7. Для таблицы вычитания и умножения проводим аналогичные действия из пункта 3. 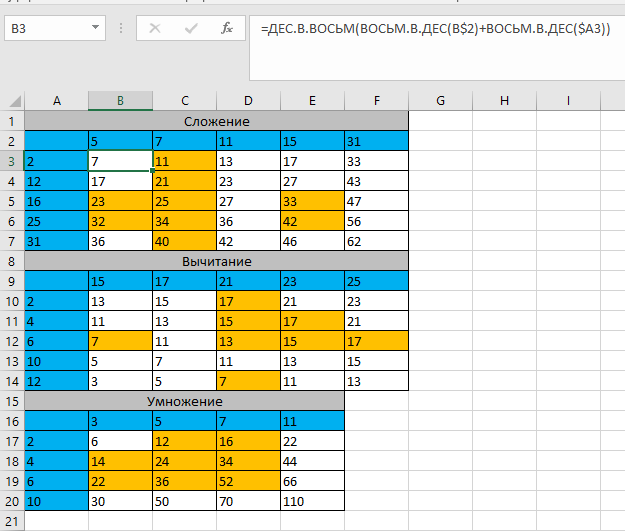 8. Отформатировать таблицы. 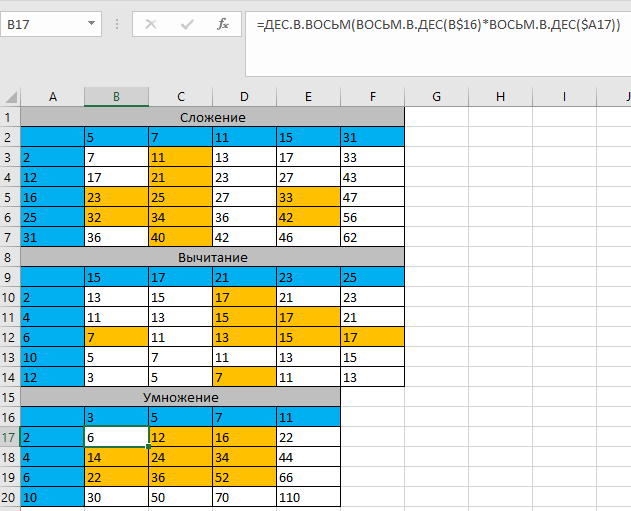 Задание 4 Для заданной таблицы, построенной на основе наблюдений метеостанции г. Екатеринбурга, определить: – минимальное месячное количество осадков за три года; – суммарное количество осадков, выпавшее за три года; – среднемесячное количество осадков по каждому году; – среднемесячное количество осадков по итогам трехлетних наблюдений; – максимальное месячное количество осадков по итогам трехлетних наблюдений; – количество засушливых месяцев за все 3 года, в которые выпало меньше 10 мм осадков; – количество месяцев в каждом году с осадками в пределах нормы (> 20 мм; < 80 мм); – количество месяцев в каждом году с осадками вне нормы(< 10 мм; > 100 мм); – построить столбчатую диаграмму по данным наблюдения за осадками в течение трех лет, позволяющую провести сравнение количества осадков. Порядок выполнения работы 1. Дать рабочему листу название «Погода». 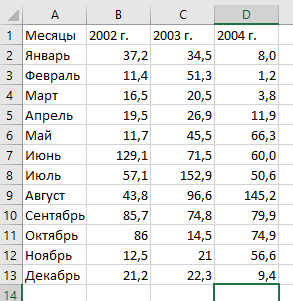 2. Для выполнения заданий использовать функции МИН; МАКС; СРЗНАЧ; СУММ категории Статистические. 3. Для выполнения заданий 6, 7, 8 – функцию СЧЁТ ЕСЛИ,которая подсчитывает количество непустых ячеек внутри интервала, удовлетворяющих заданному критерию. При ее использовании необходимо задать: интервал поиска (диапазон ячеек) и критерий подсчета (условие). Функция СЧЁТ ЕСЛИ имеет только два аргумента! Например, = СЧЁТЕСЛИ(А1:С15;”< 25”). 4. Отформатировать таблицу по своему усмотрению. 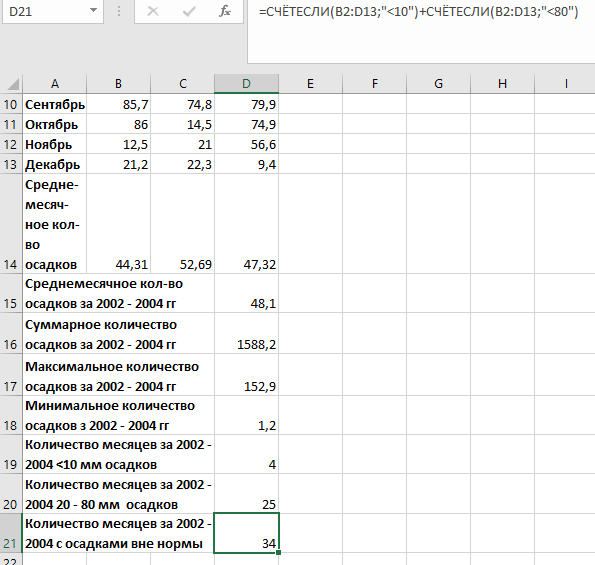 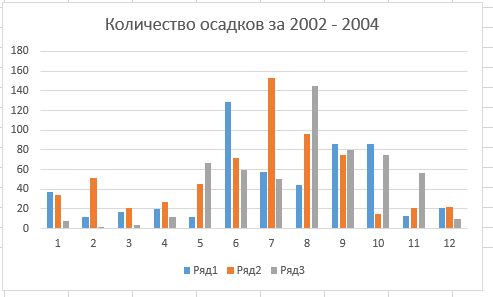 Лабораторная работа 4 РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ ПРОГРАММНЫМИ СРЕДСТВАМИ EXCEL Цели работы 1. Научиться использовать инструмент Подбор параметра для решения нелинейных уравнений вида f (x) = 0. 2. Освоить программный инструмент Поиск решения для решения систем нелинейных уравнений в среде Excel. 3. Освоить программные средства для поиска координат и значений экстремумов функции одной переменной с помощью инструмента Поиск решения. Задание 1 Найти все корни уравнения. Порядок выполнения работы 1. Дать рабочему листу название «Уравнение». 2. Настроить текущий документ Еxcel на вычисления с заданной точностью, открыв Настройку панели быстрого доступа и выбрав Другие команды. На вкладке Формулы задать предельное число итераций, равное 10000, и относительную погрешность, равную 0,000001. 3. Найти решение нелинейного уравнения в два этапа. Этап – ЛОКАЛИЗАЦИЯ КОРНЕЙ 4. Создать таблицу значений функции f (x) для х Î [-2,5; 2,5], шаг изменения 0,1. 5. Построить график функции f (x) (тип – График). 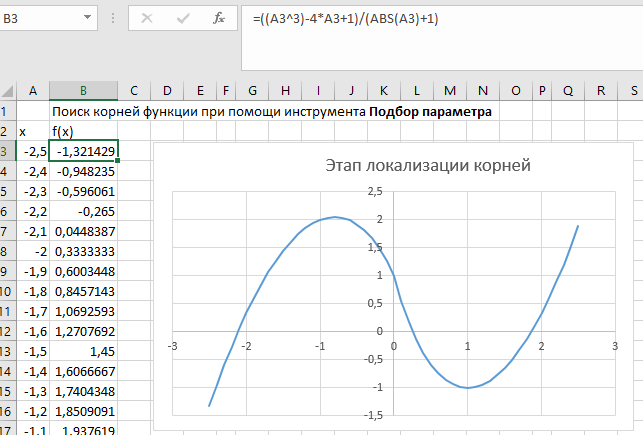 6. Основываясь на данных таблицы и графика, выделить интервалы, на которых функция меняет знак (существует корень). Этап – УТОЧНЕНИЕ КОРНЕЙ 7. Задать начальные приближения к корням – точки из отрезков локализации корней, например: -2,2; 0 и 1,5. Ввести эти значения в ячейки F16, F17 и F18 соответственно. 8. В ячейку G16 ввести формулу =(F16^3-4*F16+1)/(ABS(F16)+1) и с помощью маркера заполнения размножить эту формулу в ячейки G17 и G18. 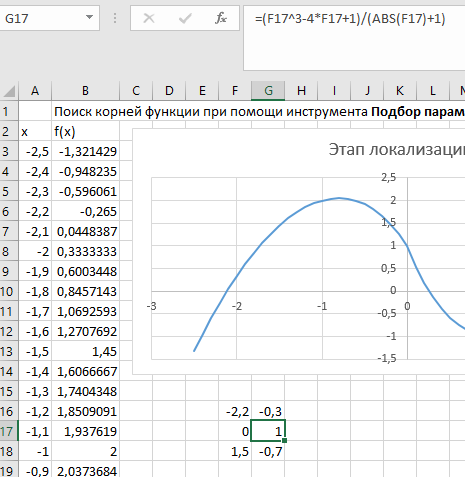 9. На вкладке Данные выбрать Анализ «что-если», открыть диалоговое окно Подбор параметра и заполнить его поля: в поле Установить в ячейке ввести G16 (в этом поле дана ссылка на ячейку, в которую введена формула, вычисляющая значение левой части уравнения); в поле Значение ввести значение 0 (здесь указывается правая часть уравнения); в поле Изменяя значение ячейки ввести F16 (в этом поле дана ссылка на ячейку, отведенную под переменную). После нажатия кнопки OK средство подбора параметра находит приближенное значение корня с заданной точностью. 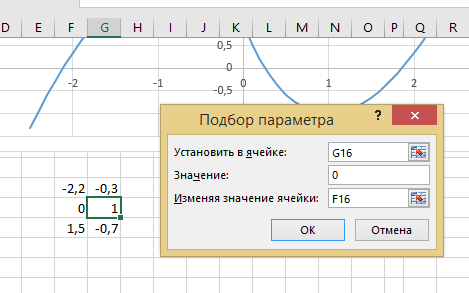 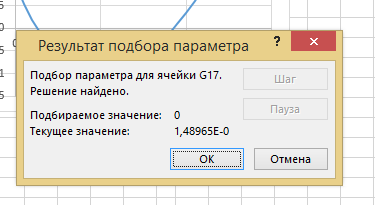 10. Повторить указанные в п. 9 действия для ячеек G17, F17 и G18, F18 соответственно. Ячейки F16:F18 содержат значения корней уравнения, а ячейки G16:G18 – значения функции в этих точках, близкие к нулю. 11. Оформить созданный лист заголовками и комментариями, как в образце. Задание 2 Найти решение системы нелинейных уравнений Порядок выполнения работы 1. Дать рабочему листу название «Система». 2. Преобразовать уравнения системы относительно переменной у, получив две полуокружности в положительной и отрицательной полуплоскостях, пересекающих прямую. 3. Столбец А (аргумент x) заполнить с помощью арифметической прогрессии на интервале [– 1,7; 1,7] с шагом 0,1. 4. Столбцы B, C, D озаглавить как y1, у2, у3 и заполнить формулами, соответствующими полуокружностями прямой, используя относительную адресацию и маркер заполнения. 5. Построить графики функций системы уравнений для диапазона А2:D36 в одной системе координат и определить интервалы локализации корней. 6. Отредактировать диаграмму, согласно образцу. 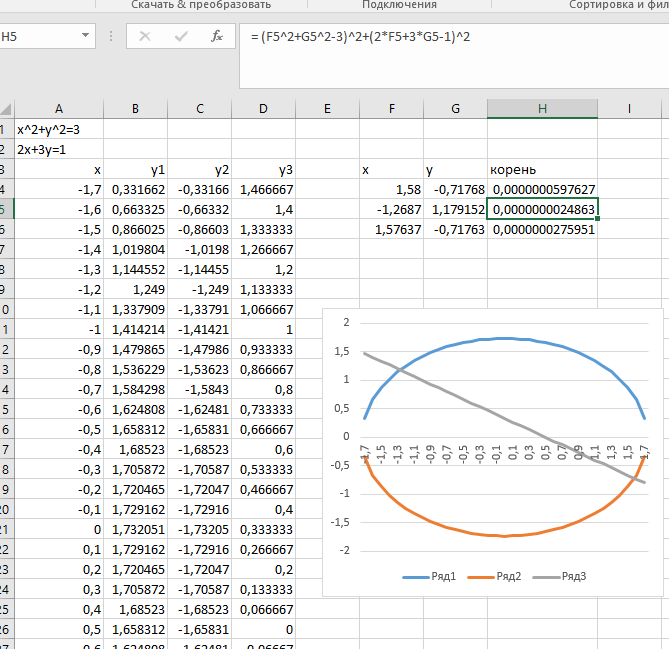 7. На втором этапе – УТОЧНЕНИЕ КОРНЕЙ – найти корни системы уравнений с помощью инструмента Поиск решения. 8. Для нахождения первого корня в ячейку F25 ввести начальное приближение для первого корня по х. В ячейку G25 –начальное приближение для первого корня по у. В ячейку H25 ввести формулу = (F25^2+G25^2–3)^2+(2*F25+3*G25–1)^2 9. Чтобы получить уточненное значение первого корня, открыть диалоговое окно Поиск решения вкладки Данные. В поле Изменяя ячейки ввести диапазон ячеек F25:G25. В группе Равной установить переключатель в положение Значению, в поле ввода которого ввести 0. Убедитесь, что в диалоговом окне Параметры поиска решения снят флажок Линейная модель. Затем нажать кнопку Выполнить и получить приближенное решение в ячейках F25 и G25, а в ячейке H25 достаточно близкое к нулю значение и с заданной точностью приблизились к точке пересечения окружности с прямой линией. Если в ячейке H25 будет большое число,то решение найдено неверно. Задание 3. Найти экстремумы функции Порядок выполнения работы: 1. Дать рабочему листу название «Экстремум». 2. Задав значения аргумента (столбец А) и рассчитав значения функции (столбец В), построить график функции и определить интервалы локализации экстремумов. 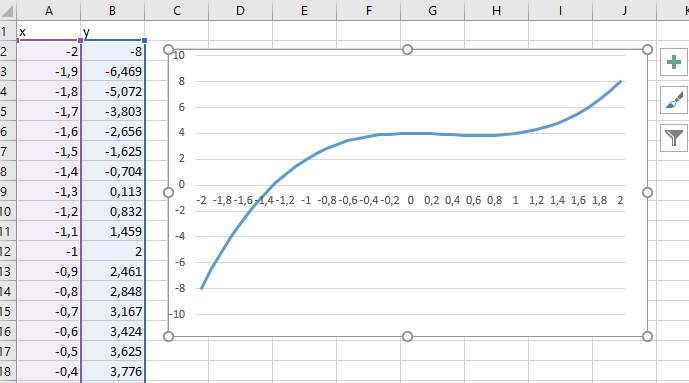 3. На этапе – УТОЧНЕНИЕ ЭКСТРЕМУМОВ – найти уточненные значения координат экстремумов и значения функции в этих точках с помощью инструмента Поиск решения. 4. Для нахождения первого экстремума (максимума) в ячейку F17 ввести начальное приближение, в ячейку G17 ввести формулу =F17^3 – F17^2 + 4. 5. Чтобы получить уточненное значение максимума, открыть диалоговое окно Поиск решения вкладки Данные. В поле Установить целевую ячейку ввести адрес ячейки, содержащей формулу – G17. В группе Равной установить переключатель в положение Максимальному значению. В поле Изменяя ячейки ввести адрес ячейки F17. Затем нажать кнопку Выполнить. 6. Получено приближенное значение координаты экстремума и максимальное значение функции в ячейках F17 и G17. 7. Аналогично находят второй экстремум. Но при настройке диалогового окна Поиск решения в группе Равной установить переключатель в положение Минимальному значению. 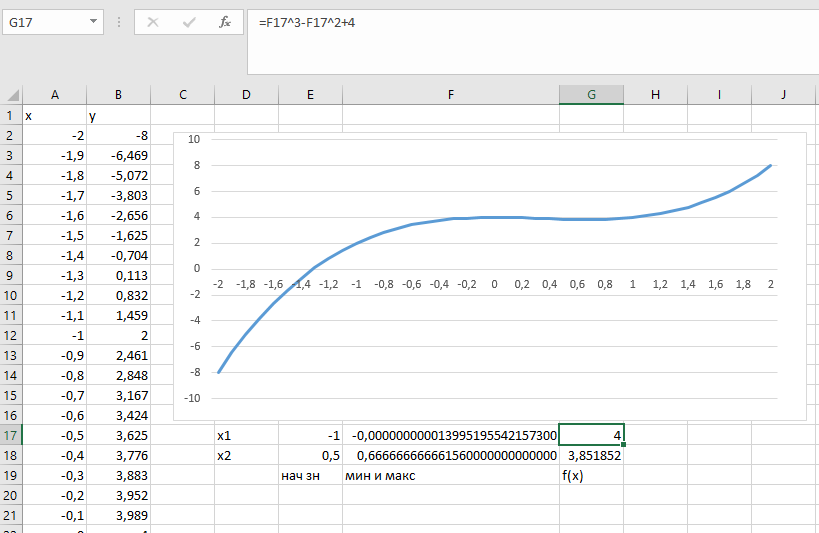 |
