Комплексті анализ (1). Таырыбы Тізбекті шегі Тексерген Таттибеков Конысбек Сатиевич Орындаан Абдикеримова А. Н. Мат21
 Скачать 2.26 Mb.
|
|
2.3 «Бір айнымалылы функцияның туындысы.» y = f(x) функциясының аргументінің екі x0– бастапқы және x – жаңа мәнін қарастырайық. Сонда x –x0 айырымы x0нүктесіндей аргументтің өсімшесі деп аталады да оны x –x0 = ∆x символымен белгілейді. Осы сияқты аргументтің екі мәніндей функция мәндерінің айырымы y – y0 = f(x) – f(x0) x0 нүктесіндегі аргумент өсімшесі деп, оны ∆y деп белгілейді. ∆x = x – x0 ∆y = f(x) –f(x0) = y – y0, x = x0 + ∆x, y = y0 + ∆y ∆y = f(x0 + ∆x) – f(x0) Анықтама. y = f(x) функциясының x = x0нүктесіндегі туындысы деп, функция өсімшесінің (∆y) осы нүктедегі аргумент өсімшесіне (∆x) қатынасының ∆x →0 еркін түрде ұмтылғандағы шегін (егер ол бар болса) айтады:  Белгіленуі:   Берілген функцияның туындысын табу процесін функцияны дифференциалдау деп аталады. Механикалық мәні.   материалды нүтенің түзу сызықты қозғалысының лездік жылдамдығы жолдың (S) уақыт бойынша туындысы. Ендеше туындының механикалық мәні қозғалыстың жылдамдығы, яғни, туынды лездік жылдамдық. Геометриялық мәні. – қисыққа жүргізілген жанаманың коэффициенті.  Осыдан y = f(x) функциясының графигіне M0(x0,y0) нүктесінде жүргізілген жанаманың теңдеуі y – y0 = f ’(x0) ∙(x – x0), ал осы нүктедегі нормаль теңдеу:  Функцияның туындысын табу амалы сол функцияны дифференциалдау деп атайды. Егер тәуелсіз айнымалының өсімшесі ∆х – ке сәйкес қарастырылып отырған функцияның алған өсімшесі ∆у – ті  (мұндағы А өсімше ∆х – ке тәуелді емес, ∆х→ 0 – да шама  (∆х) – да нөлге ұмтылады) түріне келтіруге болатын болса, берілген функция  x0 нүктесінде дифферанциалданатын функция деп аталады.Дифферциалданатын функцияның өсімшесі ∆у – тің тәуелді айнымалының өсімшесі ∆х – тен сызықтың тәуелділікте болатын бөлігі, яғни А∆х өрнегі, функциясының дифферанциалы деп аталады және  немесе  деп белгіленеді.Сонымен   , сондықтан   Дифферанциалдаудың геометриялық мағынасы: егер  функциясының х0 нүктесінде туындысы бар болса, онда х0 нүктесіндегі  функциясының дифференциалы жанама ординатының х0 + ∆х нүктесіне көшкендегі өсімшесіне тең.Функцияның мәнін жуықтап есептеу формуласы: 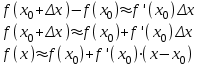 функциясының дифференциалының айрықша қасиеті сол, х тәуелсіз айнымалы болғанда да, болмаса х – тің өзі басқа бір тәуелсіз айнымалының фуекциясы болған жағдайда дифференциалдың формуласы әрқашанда өзгермей сақталады. Дифференциалдың осы сақталу қасиетін дифференциал формасының инварианттық қасиеті деп атайды. Негізгі элементарлық функциялардың туындысы. Қосындының, көбейтіндінің, бөліндінің, тұрақтының туындылары мен дифференциалдары. Туындылар мен дифференциалдарды есептеудің негізгі ережелері: (CU)’ = CU’ d(CU) = C dU (C)’ = 0 d(C) = 0 (U+V)’ = U’ + V’ d(U+V) = dU + dV (UV)’ = U’V + UV’ d(UV) = UdV + VdU   Мұндағы C – тұрақты сан, U = U(x), V = V(x) Негізгі элементарлық функцияларды дифференциалдау техникасы: Туынды күрделі функция дифференциалы 1. (lnx)’ =  (lnU)’ =  d(lnx) =  2. (logax)’ =  (logaU)’ = d(logax)=  3. (xn)’ = nxn-1 (Un)’ = nUn-1U’ d(xn) = nxn-1dx 4.    5. (ax)’ = axlna (aU)’ = aUlnU U’ d(ax) = axlna dx 6. (ex)’ = ex (eU)’ = eU U’ d(ex) = ex dx 7. (sinx)’ = cosx (sinU)’ = cosU U’ d(sinx) = cosx dx 8. (cosx)’ = - sinx (cosU)’ = - sinU U’ d(cosx)= - sinx dx 9. (tgx)’ =  (tgU)’ =  d(tgx) =  10. (ctgx)’ =  (ctgU)’ =  d(ctgx) =  11. (arcsinx)’ =  (arcsinU)’ =  d(arcsinx) = 12. (arccosx)’ =  (arccosU)’ = d(arccosx)=  13. (arctgx)’ =  (arctgU)’ =  d(arctgx) =  14. (arcctgx)’ =  (arcctgU)’ =  d(arcctgx) = Егер  шек:  немесе  тең болса, онда f функциясының  нүктесінде шексіз туындысы бар, атап айтқанда, егер  болса, плюс шексіз, ал  болса, минус шексіз туындысы бар дейді.Егер теңдіктегі шектер  (яғни  ) жағдайында қарастырылса, онда шек (ол бар болса) f функциясының нүктедегі оң жақ туындысы, ал  (яғни  ) жағдайында қарастырылса, онда шек (бар болса) f функциясының нүктедегі сол жақ туындысы деп аталады және сәйкес  арқылы белгіленеді: , .Функцияның нүктесінде туындысы бар болуы үшін,1)  және 2)  шарттарының орындалуы қажетті және жеткілікті:  . |