Комплексті анализ (1). Таырыбы Тізбекті шегі Тексерген Таттибеков Конысбек Сатиевич Орындаан Абдикеримова А. Н. Мат21
 Скачать 2.26 Mb. Скачать 2.26 Mb.
|
|
Мысал 1. Бірақ оның Расында да, Демек, функцияның Мысал 2. Шешуі. жанаманың теңдеуі y – y0 = f ’(x0) ∙(x – x0), ал осы нүктедегі нормаль теңдеу: Ол үшін функция туындысының Ендеше, жанама теңдеуі ал нормаль теңдеуі 2.4 Жоғарғы ретті туындылар мен дифференциалдар» 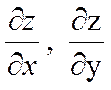 функциясының әрқайсысын х және у бойынша дифференциалдаймыз. Оларды былай белгілейміз. функциясының әрқайсысын х және у бойынша дифференциалдаймыз. Оларды былай белгілейміз.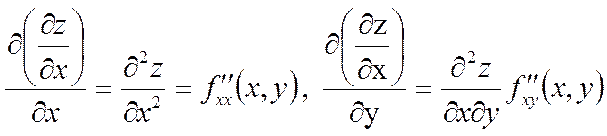 , , 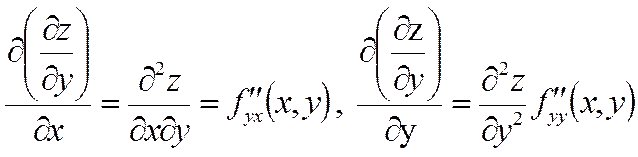 . .Жалпы айтқанда n-ші ретті туынды (n-1)-ші ретті туындыдан алынған бірінші ретті туынды болады. Әртүрлі айнымалысы бойынша алынған екінші ретті немесе жоғарғы дербес туындылар аралас дербес туындылар деп аталады. Келесі 3-ші, 4-ші тағы сол сияқты ретті туындылар да осылай анықталады. Әр түрлі айнымалылар бойынша алынған жоғары ретті туындыны аралас дербес туынды дейді. Мысал Берілген 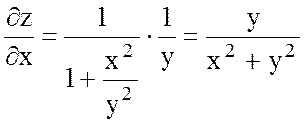 , , 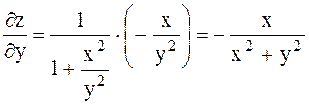 Енді екінші рет дифференциалдаймыз: 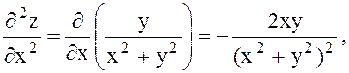 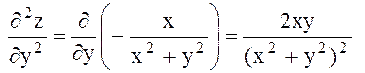 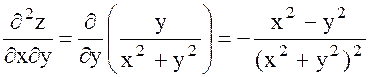 Аралас дербес туындылар жөнінде мынадай теорема орындалады. Аралас дербес туындылар жөнінде мынадай теорема орындалады.Теорема 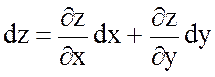 , ,мұндағы Егер немесе, аралас туындылардың өзара тең болатынын ескеріп, теңдігіне келеміз. Үшінші ретті дифференциал 2.5 «Дифференциалданатын функциялар үшін орта мән туралы теоремалар» Ферма теоремасы. Егер Бұл теореманың геометриялық мәні мынадай: Функцияның ең үлкен не ең кіші мән қабылдайтын нүктелерінде қисыққа жүргізілген жанамалар ОХ өсіне параллель болады. Ролль теоремасы.(бұл теорема Ферма теоремасының салдары) Егер Бұл теореманың геометриялық мәні мынадай: Егер 2.Лагранж теоремасы.(мөлшерлі өсімшелер туралы теорема )Егер Бұл теореманың геометриялық мәні мынадай: функция графигінде ең болмағанда бір нүкте табылып, онда жүргізілген жанама доғаның шеткі нүктелерін қосатын хордаға параллель болады. Коши теоремасы.Егер f(x) және Бұл теореманың геометриялық мәні мынадай: Бұл формула хорданың бұрыштық коэффициенті мен ішкі нүктеде жүргізілген жанаманың бұрыштық коэффициенттерінің тең екендігін көрсетеді, яғни хорда мен жанаманың параллельдігін көрсетеді. 3. Лопиталь ережесі.Шектер теориясында анықталмағандықтарды ашу туралы айтқанбыз. Енді оларды айқындаудың жаңа, Лопиталь ережесі деп аталатын, ережесін қарастырамыз. Теорема. f(x) және онда (1) формула бойынша табылған шектерді анықталмағандықты айқындаудың Лопиталь ережесі деп атайды. Егер Ескерту: Лопиталь теоремасы 2.6 Лопиталь ережесі бойынша анықталмағандықты ашу. Тейлор формуласы    Тейлор қатары – функцияны көрсеткішті функциялар шексіз қосындысы ретінде жазу. Тейлор қатарының дербес қосындылары болып Тейлор көпмүшелігі саналады. Rn(x)=f(x)-Sn(x) Тейлор қатарының қалдық мүшесі, мұндағы Sn(x) – Тейлор қатарының алғашқы n+1 мүшесінің қосындысы. болғанда Тейлор қатары f(x) функциясына жинақты болады, яғни формуласы шығады. Бұл формуланы 1715 жылы ағылшын математигі Б.Тейлор (1685 – 1731) тапқан, х0=0 болған кезде Маклорен қатары шығады. Осыған сүйене отырып, негізгі элементар функциялардың Тейлор қатарына жіктелуін жазуға болады.    |
