Расчет линейной электрической цепи при гармоническом воздействии. Техническое задание на курсовую работу со схемами 4 Выбор варианта схемы 6
 Скачать 0.52 Mb.
|
|
Расчет линейной электрической цепи при гармоническом воздействии СОДЕРЖАНИЕ ВВЕДЕНИЕ 3 1. Техническое задание на курсовую работу со схемами 4 2. Выбор варианта схемы 6 3. Расчет простой электрической цепи 7 4. Составление системы уравнений для расчета токов и напряжений 11 5. Расчет контурных токов в сложной электрической цепи методом Крамера и обратной матрицы 12 6. Определение выражения для комплексного коэффициента передачи 14 7. Построение графиков АЧХ и ФЧХ с определением их характеристик 16 ЗАКЛЮЧЕНИЕ 21 СПИСОК ЛИТЕРАТУРЫ 22 ВВЕДЕНИЕЦелью курсовой работы является изучение базовых методов расчета электрических цепей и развитие умения применять эти методы в решении практических задач по анализу характеристик электрических цепей. Основными задачами работы являются: расчет значений номиналов элементов электрических цепей, нахождение комплексных амплитуд и мгновенных значений гармонического тока, расчет и построение частотных и переходных характеристик электрических цепей, определение основных параметров указанных величин. Методами решения являются: метод токов ветвей, метод контурных токов, методы анализа частотных и переходных характеристик линейных цепей. 1. Техническое задание на курсовую работу со схемамиВ курсовой работе требуется определить токи и напряжения в ветвях простой и сложной электрических цепей при наличии в них источников гармонического напряжения, а также АЧХ и ФХЧ четырехполюсника. Различные конфигурации схемы образуются в зависимости от положения ключей «К1 - К5», которые устанавливаются по номеру варианта, представленному в двоичном коде.  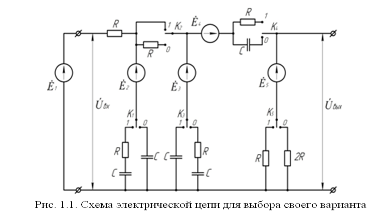 Определить величины элементов схемы рисунка 1.1 и частоту генераторов с помощью следующих формул     где N – номер варианта, n - номер элемента в схеме. В схеме, полученной в п. 1.1, исключить (замкнуть) все источники кроме 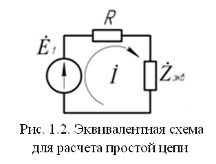 и рассчитать, используя простые преобразования цепей, ток в цепи источника . По результатам расчета построить векторную диаграмму для цепи, в которой все элементы цепи, кроме резистора R, подключенного к источнику , объединены в эквивалентное сопротивление  , как показано на рисунке 1.2. Осуществить моделирование цепи с помощью программы EWB-5.12 и определить значение тока в цепи источника , а также напряжения на сопротивлении и R.2. Выбор варианта схемыДля выбора схемы необходимо представить номер варианта в двоичной форме. Установим переключатели К1 - К5 в положения, соответствующие номеру в двоичной записи (Таблица 1). Таблица 1 - Положение ключей в схеме
Зарисуем получившуюся схему без переключателей и отсоединенных элементов. 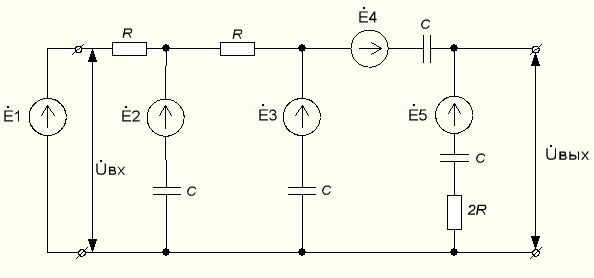 Рис.2.1. Схема электрической цепи в соответствии Определим величины элементов схемы (Рисунок 2.1) по формулам из п. 1.2, учитывая, что все генераторы в схеме имеют одинаковую частоту: R = 100·(4+0,2·4) = 480 Ом; С = 100·(5+0,2·4) = 580 пФ; Ė1 = 2·[7+(-1)1+4·0.2·4] ·е(-1)·j(25+0,2·4) = 12,4·е- j 25,8 В; Ė2 = 2·[7+(-1)2+4·0.2·4] ·еj(25+0,2·4) = 15,6·е j 25,8 В; Ė3 = 2·[7+(-1)3+4·0.2·4] · е(-1)·j(25+0,2·4) = 12,4·е -j 25,8 В; Ė4 = 2·[7+(-1)4+4·0.2·4] ·еj(25+0,2·4) = 15,6·е j 25,8 В; Ė5 = 2·[7+(-1)5+4·0.2·4] · е(-1)·j(25+0,2·4) = 12,4·е -j 25,8 В; fn = 10[7+(-1)4·0.2·4] = 78кГц. В соответствии с заданием все генераторы имеют одинаковую частоту: f1 = f2 = f3 = f4 = f5 =78кГц. Значение фазы источников  задается в градусах, а Mathcad осуществляет расчеты в радианах. Вследствие этого величину фазы генераторов умножаем на величину  .3. Расчет простой электрической цепиВ схеме (рис. 2.1) замкнем все источники кроме 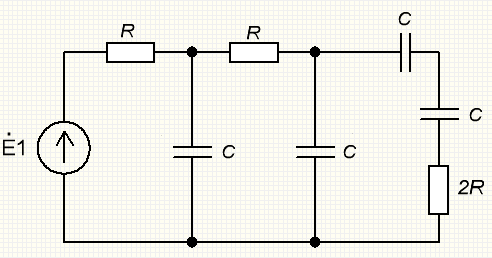 (см. рис. 3.1): Рис.3.1. Схема цепи с одним источником Преобразуем данную схему, объединив все элементы цепи, кроме R, подключенного к источнику 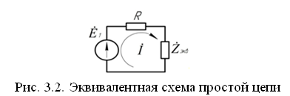, в эквивалентное сопротивление   Рассчитаем, используя простые преобразования цепей, ток в цепи источника , а также напряжения на R и .Значение тока в цепи источника определяется по формуле закона Ома для полной цепи:  Эквивалентное сопротивление  экв определим, используя формулы для последовательного и параллельного соединения нескольких элементов. Напряжение на сопротивлении экв определяется по формуле: эквНапряжение на сопротивлении R определяется по формуле:  Все необходимые расчеты проведем в среде Mathcad 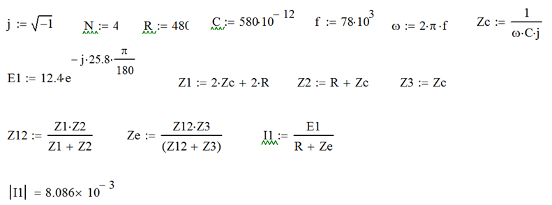      По полученным значениям строим векторную диаграмму в масштабе для  ,  , , Ė1, имея в виду, что в цепи выполняется второй закон Кирхгофа, т.е. ,а для векторов это отражается в виде их векторной суммы. Построим векторную диаграмму. 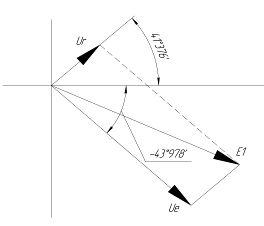 Проведем моделирование режима работы простой цепи с помощью программы EWB 5.12. Соберем простую цепь в соответствии с рис. 3.1. Выберем номиналы резисторов и конденсаторов в соответствии с заданием. Установим величину ЭДС, частоты и начальной фазы генератора, учтем что в программе EWB 5.12 гармоническое напряжение задается в синусоиде и увеличим угол на 900. Результаты моделирования в EWB: 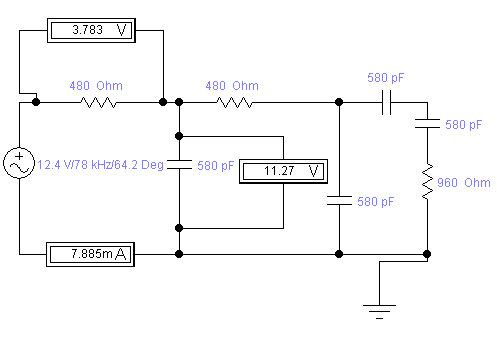 Результаты сравниваем с рассчитанными ранее значениями аргументов  Сравнение результатов расчета и моделирования простой схемы
Малая погрешность расчетов позволяет сделать вывод о достоверности результатов. 4. Составление системы уравнений для расчета токов и напряженийДля определения токов и напряжений на всех элементах цепи при известных значениях R, C и E необходимо составить систему уравнений по методу контурных токов. Данный метод основан на использовании только второго закона Кирхгофа, что позволяет уменьшить число уравнений, которые нужно решать совместно. Схема электрической цепи, токи в которой необходимо определить представлена на рис. 4.1. 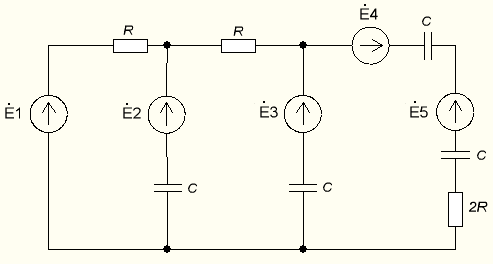 Рис.4.1 Схема цепи для расчета токов и напряжений Вначале составляется граф данной электрической цепи, по которому выбираются независимые контуры и задаются контурные токи. Для этих контуров составляются уравнения по второму закону Кирхгофа с учетом совместного влияния одного контура на другой. Направления обхода во всех контурах выбирают одинаковыми. 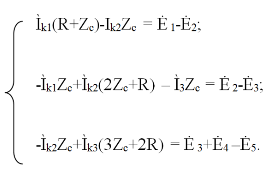 5. Расчет контурных токов в сложной электрической цепи методом Крамера и обратной матрицыРасчеты проведенные в среде Mathcad 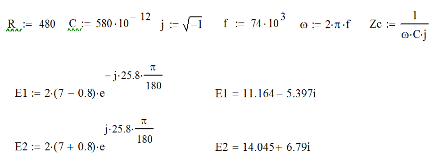  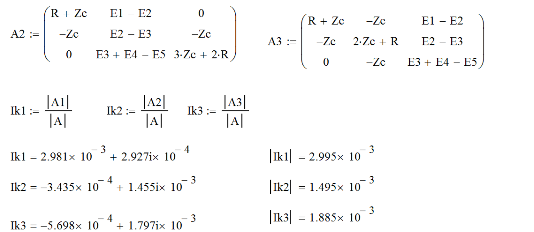 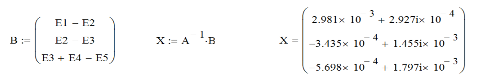 Проведем моделирование режима работы сложной цепи с помощью программы EWB 5.12. Соберем цепь в соответствии с рис. 4.1. Выберем номиналы резисторов и конденсаторов в соответствии с заданием. Установим величины ЭДС, частоты и начальной фазы генераторов. При установке начальной фазы у генераторов нужно учесть, что в программе EWB 5.12 гармоническое напряжение задается в синусоиде, а следовательно угол надо увеличить на 900. Результаты моделирования: 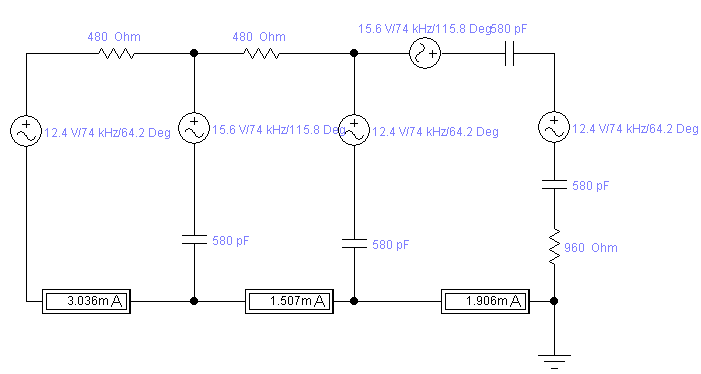 Сравним результаты вычисления токов методом Крамера, методом обратной матрицы и результаты моделирования. Сравнение результатов расчета и моделирования сложной схемы
Малая погрешность расчетов позволяет сделать вывод о достоверности результатов. электрический напряжение контурный ток 6. Определение выражения для комплексного коэффициента передачиВ соответствии с заданием необходимо определить комплексный коэффициент передачи простой цепи, рассмотренной ранее в пункте 3 данной работы (см. рис. 3.1). Комплексный коэффициент передачи 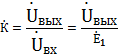 заданной цепи определяется с помощью формулы: Напряжение  определим, используя метод контурных токов. Составим систему уравнений по методу контурных токов Выразим из первого уравнения системы (5.1) ток I1 :  ;Подставим полученное выражение тока I1 во второе уравнение системы и выразим I2:   .Подставим полученное выражение тока I2 в третье уравнение системы (5.1), из которого найдем контурный ток I3. 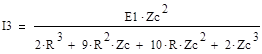  Напряжение на выходе цепи в схеме (рис. 3.1) равно: Следовательно комплексный коэффициент передачи равен:  Получаем выражение для комплексного коэффициента передачи цепи: 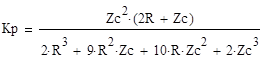  (5.2)7. Построение графиков АЧХ и ФЧХ с определением их характеристикДля построения амплитудно-частотной характеристики определим выражение для АЧХ, которая определяется как модуль комплексного коэффициента передачи:  .Для построения фазо-частотной характеристики (ФЧХ) определим аргумент комплексного коэффициента передачи:  .После определения выражений для АЧХ и ФЧХ осуществим построение их графиков с использованием соответствующих операций из программы Mathcad. По условию задания при анализе АЧХ и ФЧХ цепи для всех вариантов устанавливается  и   - частота изменений с интервалом 100 Гц.Расчеты проведенные в среде Mathcad  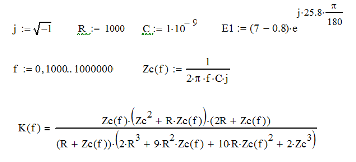 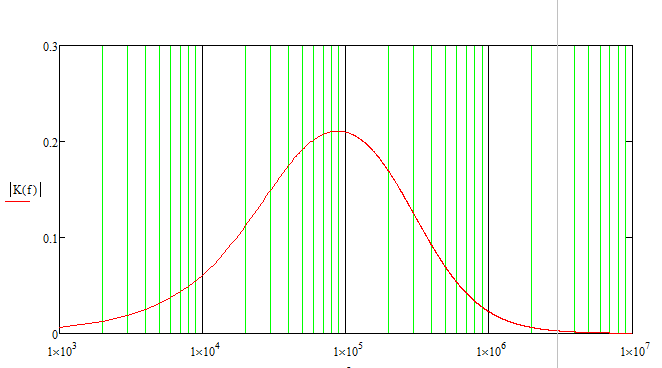 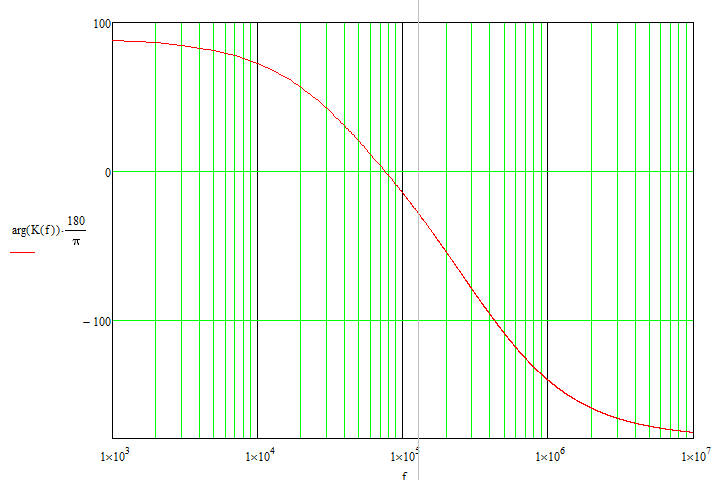 Для сравнения построим АЧХ и ФЧХ, используя программный симулятор EWB-5.12.  Анализ характеристик показывает, что данная цепь является полосовым, то есть в диапазоне частот от 29,6 до 242,8 кГц фильтр обеспечивает прохождение колебаний без заметного ослабления и значительное ослабление за пределами данной полосы частот. По графикам определяем верхнюю граничную частоту полученного фильтра, на которой коэффициент передачи составит  .f(н)0.707 = 29,6 кГц. f(в)0.707 = 242 кГц. Для вычисления коэффициента прямоугольности воспользуемся формулой:  где  – полоса частот по уровню сигнала  , – полоса частот по уровню сигнала  . ЗАКЛЮЧЕНИЕВ процессе выполнения курсовой работы были освоены методы расчета схем с использованием вычислительной техники, компьютерного схемотехнического моделирования и экспериментальных исследований электрических цепей На основе полученных знаний в процессе выполнения курсовой работы были освоены следующие темы дисциплины: переходные процессы, цепи гармонического тока; частотно-избирательные цепи; методы расчетов электрических цепей; электрические фильтры. Все это обеспечивает студентов необходимой подготовкой для предстоящих инженерных исследований. СПИСОК ЛИТЕРАТУРЫ1. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. – М.: Высшая школа, 1996. – 528 с. 2. Матвеев Б. В. Общая электротехника и электроника: учеб. пособие/Б. В. Матвеев. Воронеж: ГОУВПО «Воронежский государственный технический университет», 2009. Ч. 1. 164 с. 3. Карлащук В.И. Электронная лаборатория на IBM PC: Программа Electronics Workbench и ее применение. – М.: Издательство «Солон-Р», 1999. – 506 с. 4. Макаров Е.Г. Mathcad: Учебный курс. – СПб.: Питер, 2009. – 384 с. |
, В
, В