Задача БАДЕР. Технологический университет центр послевузовского обучения московский государственный институт стали и сплавов
 Скачать 179.5 Kb.
|
|
(ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ) ЦЕНТР ПОСЛЕВУЗОВСКОГО ОБУЧЕНИЯ МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ СТАЛИ И СПЛАВОВ Менделев А.В., Костюхин Ю.Ю. СБОРНИК ТИПОВЫХ ЗАДАЧ по курсу: "Микроэкономика" Москва - 2003 г. Раздел 1. Микроэкономика Показатели, используемые при решении задач.
Задача 1.1. Кривая спроса на товар описывается следующим уравнением: QD=500-2P. Кривая предложения имеет вид: QS=200+4P. Определить равновесную цену и объем товара. Решение: 1. Рассчитаем равновесную цену товара: QD=QS: 500-2P=200+4P; P=50 ден.ед. 2. Определим объем товара: Q=500-2*50=400 ед. Задача 1.2. Владелец редкого собрания изданий планирует продать имеющиеся у него книги. Кривая спроса на данные книги имеет вид: QD=600-30P. Определить, какую цену должен установить владелец библиотеки для получения максимального, при условии, что все книги обладают равной стоимостью. Задача 1.3. Фирма работает по технологии, описываемой производственной функцией: Q=L0,5K0,5. Цена труда составляет 5 ден. ед., цена капитала - 10 ден. ед. Определить среднюю производительность труда при нахождении фирмы в состоянии равновесия. Решение: 1. Определим предельную производительность труда: MPL=dQ/dL=0,5(K/L)0,5. 2. Рассчитаем предельную производительность капитала: MPK=dQ/dK=0,5(L/K)0,5. 3. Запишем условие равновесия фирмы: MPL/MPK=rL/rK; Отсюда, K/L=0,5. 4. Определим среднюю производительность труда: APL=Q/L=(K/L)0,5=0,71. Задача 1.4. Технология фирмы описывается производственной функцией: Q=L0,4K0,6. Бюджет фирмы - 400 ден. ед. Цена труда и капитала составляют, соответственно, 3 и 6 ден. ед. Определить, при каких объемах использования труда и капитала выпуск фирмы будет максимальным, а также равновесный объем выпуска продукции фирмы. Задача 1.5. Известна функция полезности потребителя: U=QAQB. Бюджет потребителя 72 ден. ед. При сложившихся ценах потребитель покупает два набора благ: QA=9, QB=2 и QA=3, QB=6, потому, что признает их равно полезными. Определить оптимальные с точки зрения покупателя объемы закупок товаров A и B и величину роста общей полезности набора. Решение: 1. Равная полезность наборов означает, что обе указанные комбинации лежат на одной кривой. Определим полезность наборов: U0=QAQB=2*9=3*6=18. 2. Построим бюджетную линию по двум точкам: M=PAQA+PBQB; 72=9PA+2PB; 72=3PA+6PB; Отсюда, 72=6QA+9QB. 3. Определим предельную полезность товара А: MUA=dU/dQA=QB. 4. Рассчитаем предельную полезность товара B: MUB=dU/dQB=QA. 5. Запишем условие равновесия потребителя: MUA/MUB=PA/PB; Отсюда, QA/QB=1,5. 6. Подставим полученное выше соотношение в бюджетное уравнение потребителя. Получим: QA=6; QB=4. 7. Определим полезность нового набора товаров А и В: U1=QAQB=6*4=24. 8. Прирост полезности составит: U1-U0=24-18=6. Задача 1.6. В результате повышения цены товара с 4 до 6 ден. ед., объем спроса сократился с 10 до 6 ед. Определить коэффициент прямой эластичности спроса по цене при условии неизменности остальных факторов, влияющих на спрос. Решение: 1. Определим коэффициент прямой эластичности спроса по цене: eD=(QD/QD)(P/P)=(-4/10)(4/2)=-0,8. Задача 1.7. Равновесная цена товара составляет 0,75 ден. ед. Ежегодно продается 750 ед. товара. Прямая эластичность спроса по цене составляет -0,4. Определить линейную функцию спроса на товар. Задача 1.8. На мировом рынке металла действует свободная конкуренция, а равновесная цена на нем составляет 9 долл. за унцию. Предложение товара для импорта в США по этой цене неограниченно. Предложения отечественных производителей и спрос на товар на разных уровнях цен представлен ниже.
Определить: Какова цена на рынке США и каков объем импорта. Решение. Сначала определяем кривые спроса и предложения 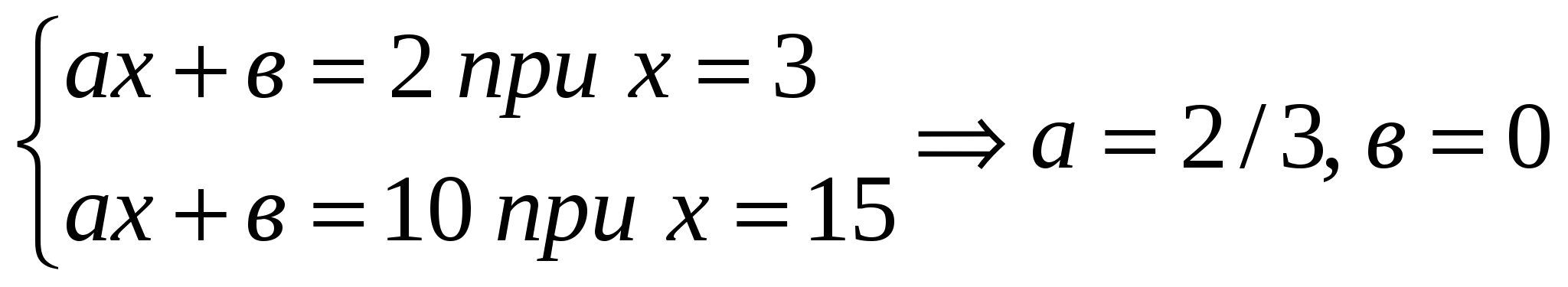 Предложения характеризуется следующей кhивой QS=2/3Р  Спрос характеризуется кривой Qd=40-2P Равновесная без учета импорта составит  за унцию.т.о. цена на рынке без введения ограничений на импорт составит 9$ за унцию. QS=2/39=6 млн. фунтов Qd=40-18=22 млн. фунта Qimport=22-6=16 млн. фунтов. Задача 1.9. Использую данные в задаче 1.8., определить:
Решение: Цена импорта при тарифе в 9$ за унцию составляет 9+9=18$, т.е. это запретительные тарифы, т.е. спрос удовлетворяется только внутренним предложениям и цена равна 15$ за унцию. При соглашении о добровольном ограничения импорта установится следующее равенство  Задача 1.10. Предложения сахара в США характеризуется кривой QS= -7,46+0,92Р, а спроса Qd=22,8-0,23Р Мировая цена составляет 12,5 цента за фунт. Импорт в США ограничен уровнем 3,8 млрд. фунтов. Определить цены на сахар. Решение: 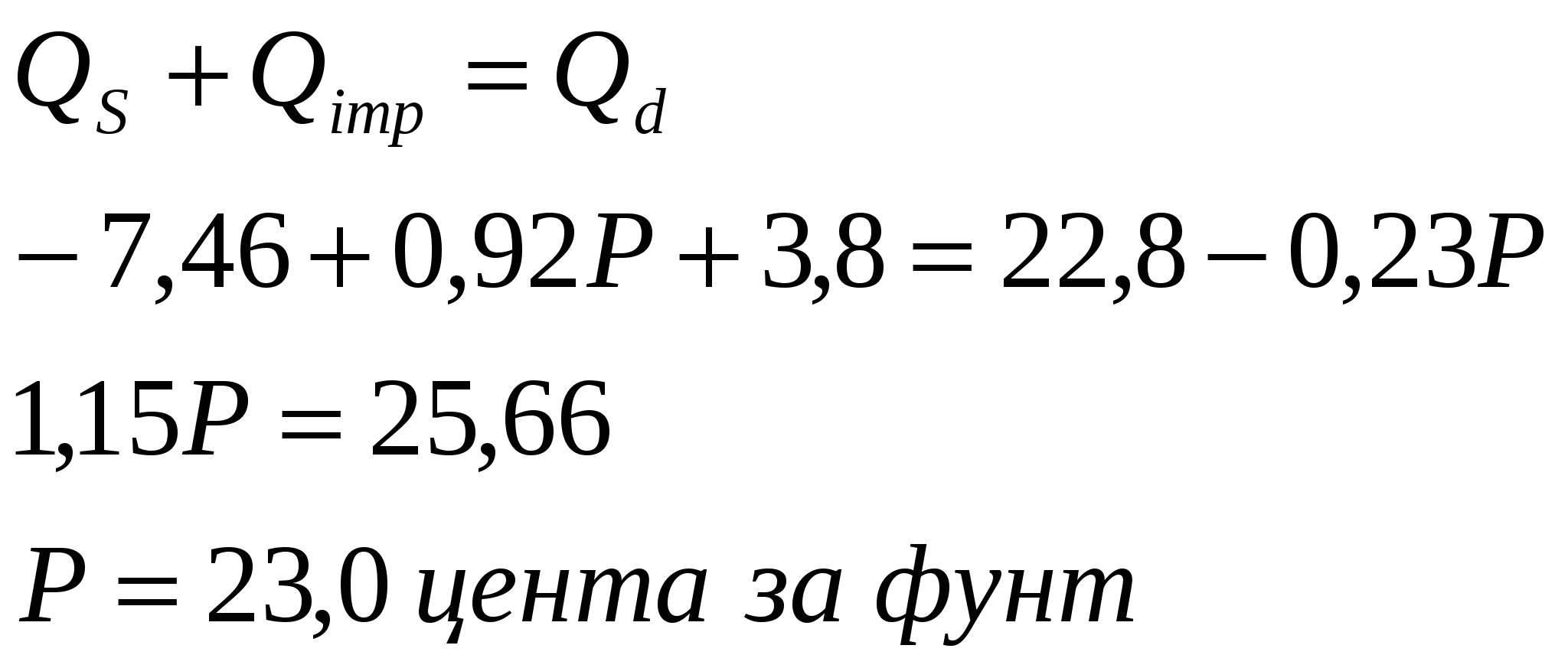 На конкурентном рынке существует явная зависимость между ценой и объемом предложения. Эта зависимость выражена кривой предложения, которая совпадает с кривой предельных издержек производства для отрасли в целом, т.к. в конкурентной отрасли экономическая прибыль равна R – плата за труд, ресурсы и капитал и стремится к нулю. Задача 1.11. Предложение на рынке пшеницы в 1981 году в США составило QS=1800+240Р, а спрос Qd=1550-266Р. В связи со значительным падением внешнего спроса на зерно, равновесная цена на внешнем рынке составила 1,8$/бушель
Решение:   Задача 1.12. Внутренний спрос на пшеницу равен QДI= 1000-46р., где QДI – кол-во бушелей пшеницы в млн.; Р – цена за бушель в долларах; Внешний спрос на пшеницу равен QД1=2550-220Р, где QL1 – количество бушелей (в млн.) на которое существует спрос за рубежом. Определить совокупный спрос. Решение.         Рис. . Совокупный спрос на пшеницу. Совокупный спрос определяется QД=QДД+QД1=(1000-46р)+(2550-220р)=3550-266р Однако при любых значениях цен выше точки С  внешний спрос отсутствует (происходит замещение пшеницы другими зерновыми культурами и остается только внутренний спрос), т.е. совокупный спрос имеет излом в точке С.Таким образом решение задачи можно записать следующим образом:  Задача 1.13. Кривая спроса на продукцию фирмы (средней выручки) представлена в виде:  где Q – недельный выпуск, Р – цена в центах/ед.Функция издержек фирмы имеет вид С=50Q+30 000 Предположим, фирма максимизирует прибыль а) Каковы объем производства продукции, цена и прибыль в неделю. б) Правительство вводит налог в размере 10 центов на ед. продукции. Каковы последствия. Решение: Объем производства оптимален, если предельная выручка равна предельным издержкам. Если Р=а-bQ=100-0,01Q, то  Р=75, прибыль=250075-502500-30000=187500-125000-30000=32500 центов в неделю При введении 10 центового налога от объема продаж MR=90-0,02Q 90-0.02Q=50 Q=2000 Снижение объема продаж на  ; , Р2=80(потребителя)Прибыль  Цена для потребителя возрастет  Прибыль снизится на  Задача 1.14. Рынок труда ассистентов преподавателей (ТА) в основных университетах США можно охарактеризовать как монопсодию. Пусть спрос на труд ТА равен W=30000-125n, где W – з/п годовая, n – число принятых на работу ТА. Предложение труда ТА равно W=1000+75п Определить: а) Если университет воспользуется своим положением монопсодиста, то какое число ТА получат работу? Какова при этом будет их з/п. б) Если кривая предложения является бесконечно эластичной при з/п 10000, то какое количество ТА получат работу. Решение:         Рис. . Монопсодия Определяем количество ассистентов преподавателей, исходя из равенства МЕ=МV, т.е. предельные расходы университета (МЕ) равны его предельной полезности (MV) 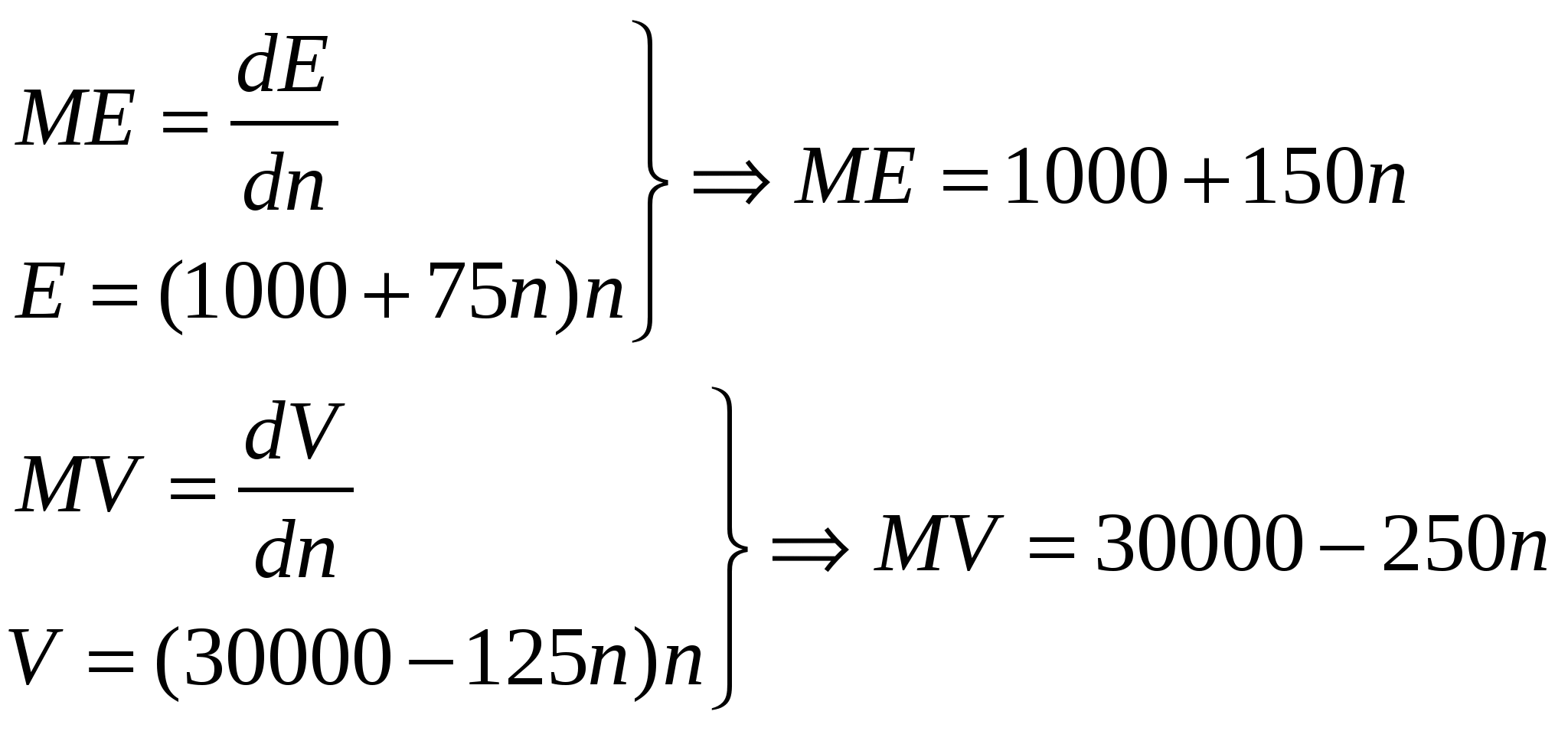 а) Исхода из равенства МЕ=МV  преподавателя, з/п=1000+7573=6475$.б) Если кривая предложения является бесконечно эластичной при з/п 10000, то  Задача 1.15. При цене товара 20 ден. ед. на рынке было 3 покупателя, имеющих прямолинейные функции спроса по цене. Первый купил 25 ед. товара и его эластичность спроса по цене была -1,5; второй купил 20 ед. товара при эластичности спроса по цене -2; третий купил 30 ед. товара при эластичности спроса по цене -2,5. Определить эластичность рыночного спроса по цене. Задача 1.16. Коэффициент перекрестной эластичности спроса на цыплят и свинину составляет 0,4. Определить, как изменится объем покупок цыплят, если при прочих равных условиях цена на свинину увеличится на 20%. Решение: 1. Запишем коэффициент перекрестной эластичности: eС=(QX/QX)/(PY/PY); Отсюда, QX/QX=eС(PY/PY)=0,4*0,2=0,08 (8%), т.е. объем покупок цыплят возрастет на 8%. Задача 1.17. В условиях совершенной конкуренции цена товара равна 160 ден. ед. Функция суммарных затрат предприятия описывается уравнением: TC=10+200Q-4Q2. Определить выпуск предприятия. Решение: 1. Выведем функцию предельных затрат предприятия: MC=200-8Q. 2. Из условия максимизации прибыли следует, что: MC=P; 200-8Q=160; Q=5 ед. Задача 1.18. Рассмотрим фирму, обладающую монопольной властью. Кривая спроса выражается как Р=100-3Q+4А1/2 Кривая совокупных издержек имеет вид С=4Q2+10Q+А Где: А – уровень расходов на рекламу; Р и Q – цена и объем выпуска соответственно. а) Найдите величину А, Q, Р которые максимизируют прибыль фирмы. б) Подсчитайте индекс монопольной власти Лернера – L=(P-MC)/P – для данной фирмы при величинах A, Q, P максимизирующих прибыль. Решение: Предельная выручка равна MR=100-6Q+4A1/2 Предельные издержки равны MC=8Q+10 Максимум прибыли достигается MR=MC  Определим объем рекламы при котором фирма получит максимальную прибыль, для этого дифференцируем прибыль по А 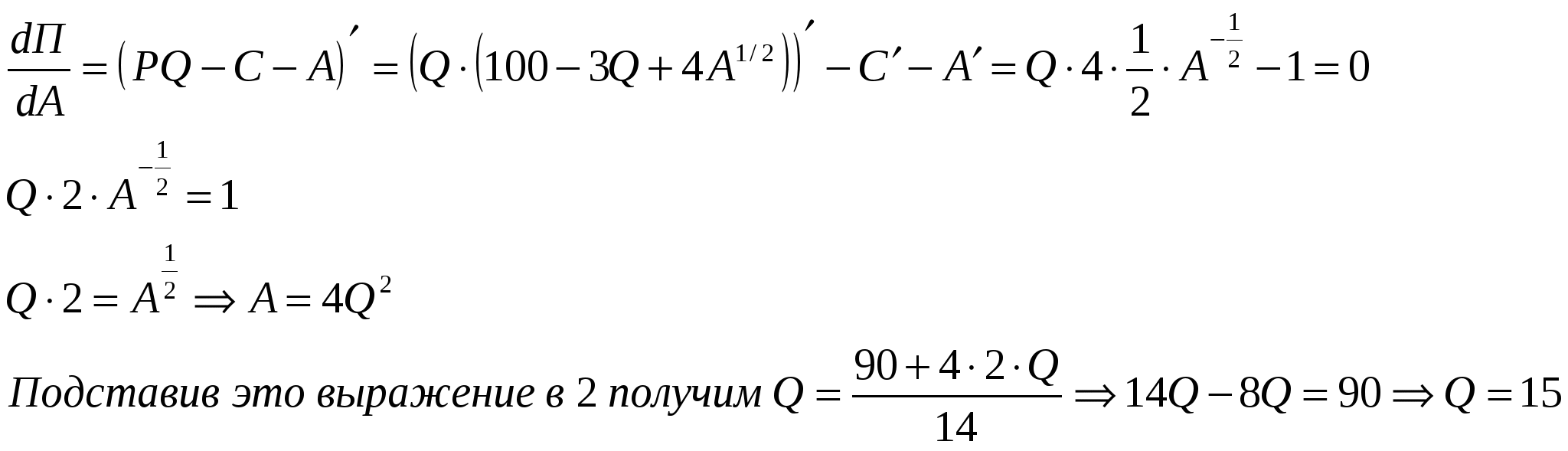 1415=90+4А1/2 А1/2=30; А=900  Задача 1.19.Рассмотрим следующую дуополию. Спрос выражается уравнением: P = 10 – Q, где Q = Q1 + Q2. Функции издержек фирм: C1(Q1) = 4 + 2Q1 и C2(Q2) = 3 + 3Q2. Фирмы ведут себя не кооперативно. Сколько фирма 1 готова заплатить за покупку фирмы 2, если сговор запрещен, а покупка нет. Задача 1.20. Функция спроса на продукцию фирмы – монополиста P = 20 – Q , функция издержек – C = Q^2 + 40. Государство вводит налог в размере 2 денежные единицы на каждую единицу продукции. Определите налоговые поступления и изменение прибыли фирмы-монополиста. Две фирмы производят товар, характеризующийся следующей кривой спроса: P = 150 – Q, их издержки равны C1 = 30Q1 и C2 = 30Q2: Где: Q1 - объем выпуска фирмы 1; Q2 - объем выпуска фирмы 2. Задача 1.21.Посчитай те прибыль в точке, где достигается равновесие Курно. Предположим, фирмы объединяются в картель. Каков будет картельный объем выпуска и прибыль каждой из фирм. Задача 1.22. Спрос монопсодиста на продукцию равен: Qd = 2000 – 15P, где Qd - объем продукции, P -цена. Предложение данной продукции на рынке равно Qs = 100 +5P. Если фирма воспользуется своим правом монопсодиста, то какой объем продукции и по какой цене она закупит. Задача 1.23.Две фирмы конкурируют с помощью цен. Функции спроса на их продукцию следующие: Q1 = 40 - 2P1 + P2 Q2 = 40 + P1 - 2P2 Предположим, что Вы являетесь управляющим одной из этих фирм, и Вы можете:
Задача 1.24.Спрос на бензин характеризуется кривой QД=40-60р, а предложение – QS=10+40р., где Q – объем бензина в млрд.л., р-цена долларов за литр. Правительство вводит акциз в размере 5,0 центов за литр. Определить % снижения потребления бензина, государственные поступления, потери производителя и потребности, а также безвозвратные потери. Решение. До введения налога существовало рыночное равновесие, т.е. QД=QS, после введения правительство хочет получить 5 процентов с литра, т.е. Pd – Рs=0,05. Объем продаж до введения налога равен: 40-60Р=10+40РР=0,3 QS=10+400.3=22 млрд. литров. После введения: 40-60(PS+0.05)=10+40PS PS=0,27$/литр.  млрд. литров, т.е. % снижение объема потребления бензина 5,45%.       Последствия введения налога на бензин (в млрд. литров). Цена покупки бензина на автоколонке возрастет с 03 до 0,32 $/литр, годовые поступления правительству (А+ В – площади) составят: 20,8х0,05=1,04 млрд. $ в год. Потери потребителей (А+С – площади) составят:  Потери производителей (В+Е – площади) составят:  Безвозвратные потери (С+Е – площади) составят: 0,012+0,018=0,03 млрд. $ в год. Обращаем Ваше внимание, что распределение потерь потребителей и производителей зависит от эластичности спроса и предложения. При менее эластичном спросе и более эластичном предложением торговые поступления правительству могут почти полностью состоять из потерь потребителей. Доля налогового бремени (Н.Г.) на потребителя =  , если спрос совершенно не эластичен, а значит Еd=0, то доля налогового бремени равна 1 и оно полностью ложится на плечи потребителей.Задача 1.25.В картель объединились 4 фирмы, имеющие следующие функции издержек: TC1 = 20 + 5Q1^2; TC2 = 25 + 3Q2^2: TC3 = 15 + 4Q3^2: TC4 = 20 + 6Q4^2: Если картель решил установить цену 25 у.ед. за единицу продукции и произвести 10 ед. продукции, как следовало бы разделить производство между фирмами. У какой из фирм наибольшие стимулы выйти из картеля, а у какой наименьшие. Задача 1.26. Компания «Элизабет» производит авиа перевозки только по одному маршруту: Москва – Гонолуну. Спрос на каждый рейс по этому маршруту задается как Q=500 – P. Издержки «Элизабет» составляют 30000 долл. на каждый рейс плюс 100 долл. на каждого пассажира. а) Какова цена, максимизирующая прибыль компании? Сколько людей воспользуются каждым рейсом. Какова прибыль компании за каждый рейс? б) Авиакомпании стало известно, что финансирование издержек за рейс составляют 41000 долл. Продолжат ли компания свою деятельность. Ответ обоснуйте. в) Компания определила, что в Гонолуну летают две разные категории клиентов. Категория А – бизнесмены QA = 260 – 0,4 P Категория В – студенты QB = 240 – 0,6 P Студентов легко выявить, компания решает брать с них другую плату. Решение.
 Для максимизации прибыли предельная выручка равна предельным издержкам, т.е.  Прибыль = 200300 – 100200 – 30000=10000
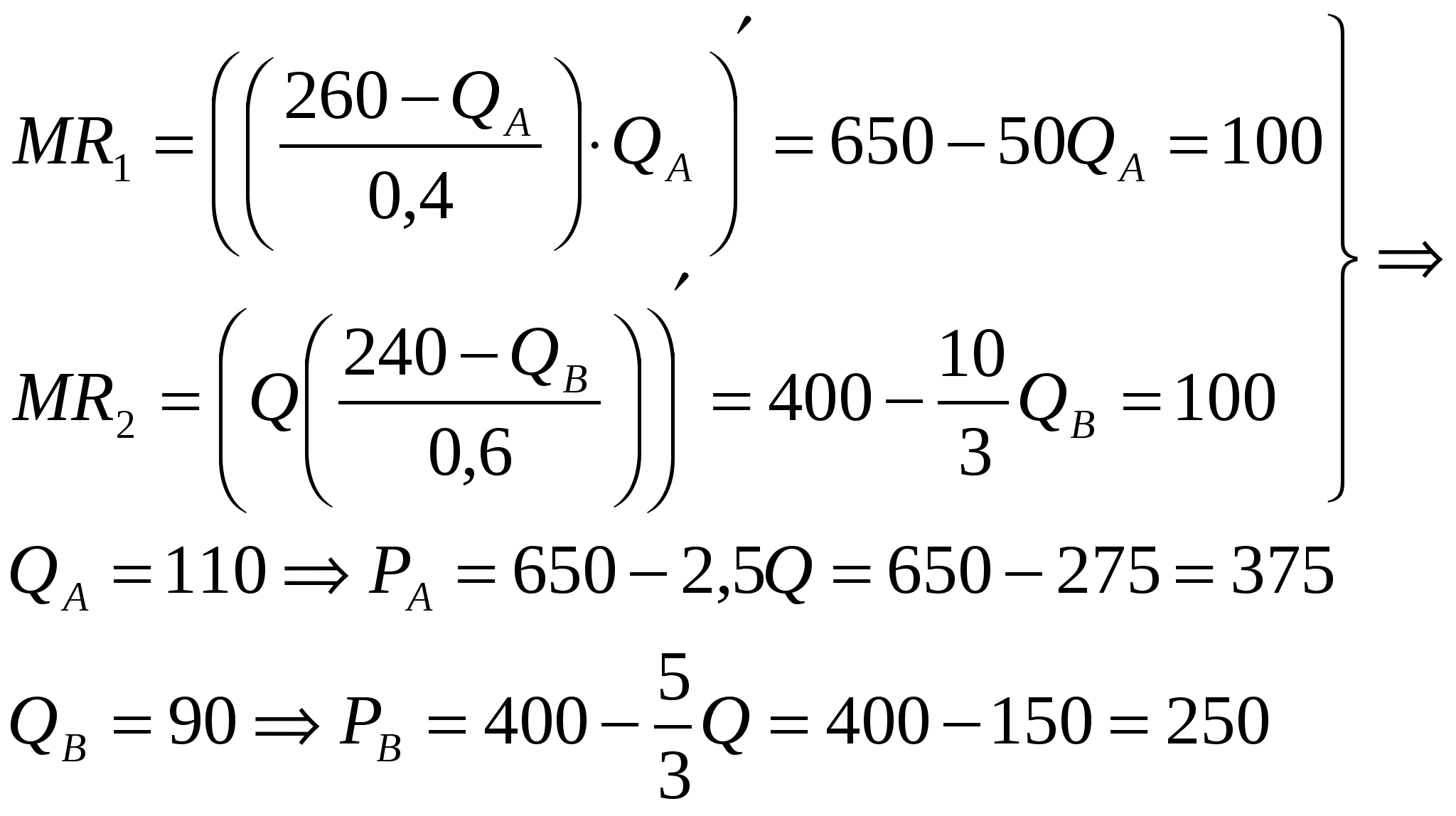  Это произошло за счет того, что спрос бизнесменов менее эластичен, чем спрос студентов. Излишек потребителя равен для бизнесменов  студентов  Излишек потребителя без разбивки на группы  Задача 1.27. Будучи владельцем единственного теннисного клуба в изолированной преуспевающей общине, вы должны решить, какие установить членские взносы и плату за аренду кортов. Имеются два вида игроков в теннис. Спрос постоянных игроков выражается функцией  , где Q – количество часов, проведенных на корте в неделю;Р – средняя плата в час, взимаемая с каждого игрока. Имеются также редкие игроки с функцией спроса  Предположим, что игроков каждого вида по 1000 человека. У Вас имеется множество кортов, поэтому фиксированные издержки равны 5000 долларов в неделю. Так как постоянные и редкие игроки выглядят одинаково, Вы должны брать с них одну и ту же плату. а) Предположим, что Вы хотите чтобы членами клуба были только постоянные игроки. В каком размере Вам следует назначить годовой членский взнос и какую плату (52 недели в году). Чтобы Ваша прибыль была максимальна и в клуб вступили только постоянные игроки. б) Приятель утверждает, что исключив одну группу игроков Вы теряете деньги. Прав ли Ваш приятель. Какие размеры взноса и средней платы максимизируют Вашу прибыль. Чему она равна. в) Предположим, что в Вашу общину приезжают 2000 молодых специалистов, и все они являются постоянными игроками. Изменится ли что-нибудь в Ваших расчетах? Решение. а) При индивидуальном спросе Q=6-P, излишек потребителя равен 18 долл. в неделю, или 936 долл. в год. Взнос, равный 936 долл. поглощает весь излишек потребителя. Еженедельная прибыль 18х1000 – 5000=13000 долл., т.к. плата за аренду корта не взимается, а членские взносы равны 936 долл. в год (18 долл. в неделю). б) Когда имеются два типа клиентов, владелец клуба максимизирует прибыль. Взнос равен излишку потребителя, оставленному после оплаты аренды (Р),  Сумма взносов всех игроков равна:  Доходы от аренды кортов равны:  Тогда максимальный доход   Предельные издержки  Совокупный доход равен  Прибыль равна 20250 – 5000=15250 в) Членский взнос, равный 18 долл. в неделю, привлечет только постоянных игроков. Доход составит 54000 долл. Прибыль 49000 долларов. Аналогичный расчет (б) получим прибыль, 39100, т.е. будут привлекаться только постоянные игроки с годовым взносом 936 долл. Задача 1.28. Многие пункты видеопроката предлагают две альтернативные схемы обслуживания: а) Двухэтапная оплата: вы вносите годовой членский взнос (4$;) и затем небольшая сумма за видеопрокат (2$) б) Прямая плата за прокат – только (4$/день). Каков смысл двухэтапной оплаты? Зачем предлагать клиенту выбор из двух схем, а не просто двухэтапную оплату. Решение. 1. Исследование двухэтапной оплаты позволяет получать излишек потребителя в размере членского взноса (40$) и устанавливать плату за прокат на уровне или чуть выше предельных издержек. Это позволяет привлекать постоянных клиентов. 2. Использование повышенной платы за прокат (4$) позволяет привлекать не только постоянных клиентов и за счет этого расширять рынок сбыта.. Задача 1.29. Вы продаете два товара – первый и второй на рынке, имеющем трех потребителей со следующими субъективными ценами: Субъективная цена (в долл.)
Издержки на производство единицы каждого товара составляют 20 долл. а) Подсчитайте оптимальные цены и прибыль в случае 1) Продажи товаров по отдельности; 2) Чистого комплектования; 3) Смешанного комплектования б) Какая стратегия более выгодна. Почему? Решение:
Объем прибыли (39,95 – 20)4 = 79,8
(79,95 – 40)3 = 119,85
Покупка  Более выгодная стратегия 3. Задача 1.30. Ваша фирма производит два товара, причем спрос на один товар не зависит от спроса на другой. Оба товара производятся при нулевых предельных издержках. Имеются четыре группы потребителя (или четыре группы потребителей) со следующими субъективными ценами:
а) Рассмотрите три альтернативные ценовые стратегии: 1) продажи товаров по отдельности; 2) чистое комплектование; 3) смешанное комплектование. Для каждой из стратегий определите оптимальные цены, которые следует назначить, а также прибыль, которая будет получена. Какая стратегия является наилучшей? б) Предположим теперь, что производство каждого товара связано с предельными издержками равными 350 ем. Какая стратегия является оптимальный теперь? Задача 1.31. Предположим, что Вы являетесь управляющим магазина и должны решить, сколько костюмов заказать на осенний сезон. Если Вы закажете 100 костюмов Ваши расходы составят 180 $/шт., а если 50 костюмов, то – 200 $/шт. Вы знаете, что будете продавать костюмы по 300 $, но не знаете общий спрос. Все не распроданные могут быть возвращены, но лишь за половину заплаченной за них цены. Решение: Без дополнительной информации Вы будете действовать, исходя из того, что вероятность продажи 100 костюмов и продажи всего 50 костюмов равна каждая 0,5. В таблице приведена прибыль, которую Вы получите в каждом случае. Таблица. Прибыль от продажи костюмов.
Без дополнительной информации Вы предпочтете 100 костюмов, если Вы безразличны к риску. При наличии полной информации Вы сможете более правильно выбрать количество костюмов. Так как оба исхода (продажа 50 или 100 костюмов) одинаково вероятны, математическое ожидание Вашей прибыли равно 50000,5+120000,5=8500$ Тогда ценность информации равна 8500-6750=1750 $. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
