C++ Лабораторная работа № 5 КТэ. Тема Циклические вычислительный процесс
 Скачать 1.28 Mb. Скачать 1.28 Mb.
|
Тема № 3. Циклические вычислительный процессЦиклическим называется алгоритм, в котором некоторая часть операция (тело цикла последовательность команд) выполняется многократно. Цикл не может быть бесконечным, т.к. алгоритм должен приводить к результату через конечное число шагов. В цикл обязательно должен входить блок проверки условия. В зависимости от того, где располагается это условие, циклы делятся на циклы типа «пока» (условие располагается перед телом цикла) и циклы типа «до» (условие располагается после тела цикла. Другой виз классификации циклов – это циклы с параметром и циклы с выходом по условию. Лабораторная работа № 5. Циклы с параметромТеорияЦикл с параметром или цикл со счетчиком используется для организации циклов, в которых можно выделить параметр с известным начальным значением, конечным значением и определить закономерность, по которому параметр изменяется при каждой итерации цикла. Итерацией цикла называется каждое повторение исполнения тела цикла Алгоритм работы оператора цикла с параметром можно представить следующей блок-схемой:  Для реализации этого алгоритма оператор цикла с параметром имеет следующий вид: for (парамер=нач.знач.; условие_работы_цикла; изменение_параметра) оператор_тела_цикла; Если тело цикла состоит более чем из одного оператора, эти операторы заключаются в фигурные скобки. Как видно из блок-схемы, в цикле for проверка выполнения условия прекращения работы цикла осуществляется перед первой итерацией, и, таким образом, возможен цикл for, тело которого не выполняется ни разу. В большинстве случаев параметр цикла с каждой итерацией изменяется на одну и ту же величину – шаг. В этом случае блок схема может быть сокращена, и, согласно ГОСТ принято еще одно обозначения цикла с параметром:  Оператор соответствующий такой блок-схеме имеет следующий вид: for (парам.=нач.знач.; парам.<=кон.знач.; парам.=парам.+шаг) Например: for (a=0; a<=3; a=a+0.1) cout<<”sin(“< Если надо считать, сколько раз проработал цикл, то шаг равен 1, и цикл можно назвать не цикл с параметром, а цикл со счетчиком. В этом случае в сокращенной блок-схеме можно не указывать шаг.  Оператор соответствующий такой блок-схеме имеет следующий вид: for (счетчик=нач.знач.; счетчик<=кон.знач.; счетчик++) Тип параметра можно описывать непосредственно в цикле, но при этом следует помнить, что за пределами цикла этот параметр не определен. Например: for (int i=1; i<=10; i++) ПримерыВычислить 10 значений d: d=a2-b2+ab-8, c  , если a<-3 , если a<-3где b= c/3, если -3a0 a+c+4, если a>0 а изменяется с шагом 4, начальное значение а равно -26 . Значение с – произвольное число. Исходные данные: Значение с – вещественное число. Результат: 10 значений d. Тестовый пример: при с=3
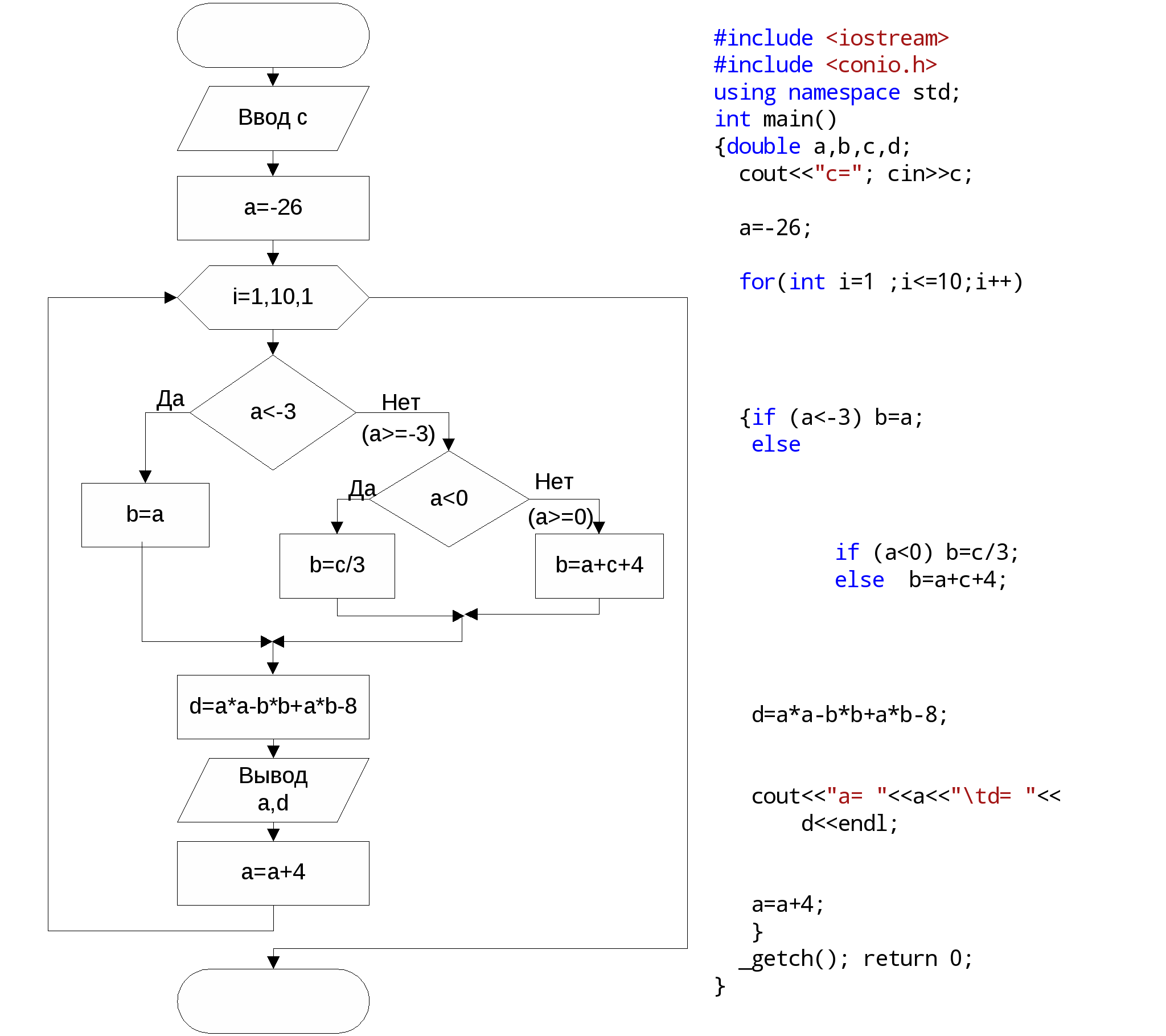 Дано натуральное n <10. Получить n-значное натуральное число. Исходные данные: количество цифр n – целый тип. Результат: d – целый тип. Тестовый пример: проверяется только количество цифр.  Вычислить сумму n вещественных чисел. Исходные данные: n - количество введенных чисел - целый тип; х – переменная, куда помещаются вводимые числа - вещественный тип. Результат: s - сумма введенных чисел – вещественный тип. При вычислении суммы выполняется операция накопления данных в одной переменной, в данном случае в переменной s: s=s+x. Эта операция должна выполняться n раз. Для того чтобы в результате первой операции накопления было получено значение первого х, переменную S предварительно надо очистить, т.е. s=0. Тестовый пример: при n=7 и последовательности:1.2, 3, 5.6, 6.1, -4, -1, 4.2, s=17.1.  В  о многих языках программирования отсутствует стандартная операция возведения в степень. Необходимо написать программу возведения в целую степень вещественного числа. о многих языках программирования отсутствует стандартная операция возведения в степень. Необходимо написать программу возведения в целую степень вещественного числа.Исходные данные: n - степень, в которую возводится число – целый тип. х - число, которое возводится в степень n – вещественный тип. Результат: p – вещественный тип. Возвести в n-ю степень число – значит перемножить это число n раз p  =xxx…x =xxx…xn Операция перемножения х похожа на операцию сложения, только знак «+» заменяется на знак «*». Как и при сложении, в результате первого действия умножения надо получить само число х, т.е., и в этом отличие от суммирования, первоначально p должно быть равно 1. Тестовый пример: При х=4 и n=5, p=1024. Ввести последовательность из n целых чисел. Найти минимальный член этой последовательности. Исходные данные: n - количество введенных чисел - целый тип; а переменная, куда помещаются вводимые числа – целый тип. Результат: min – целый тип. Поиск минимального члена последовательности чисел похож на процедуру определения лучшего результат на соревновании лыжников с раздельным стартом. Когда первый лыжник прибегает на финиш, его результат считается лучшим, т.е. в min записывается этот результат. Затем, когда прибегает очередной лыжник, его результат сравнивается с лучшим (min), и если этот результат меньше, то в значение min записывается этот результат. Следует обратить внимание, что первоначальное значение min не может равняться нулю, так как в результате будет получен этот ноль. Поиск максимального элемента отличается от поиска минимального только проверкой: если новое значение больше текущего максимального, в максимальное значение записывается это новое значение. 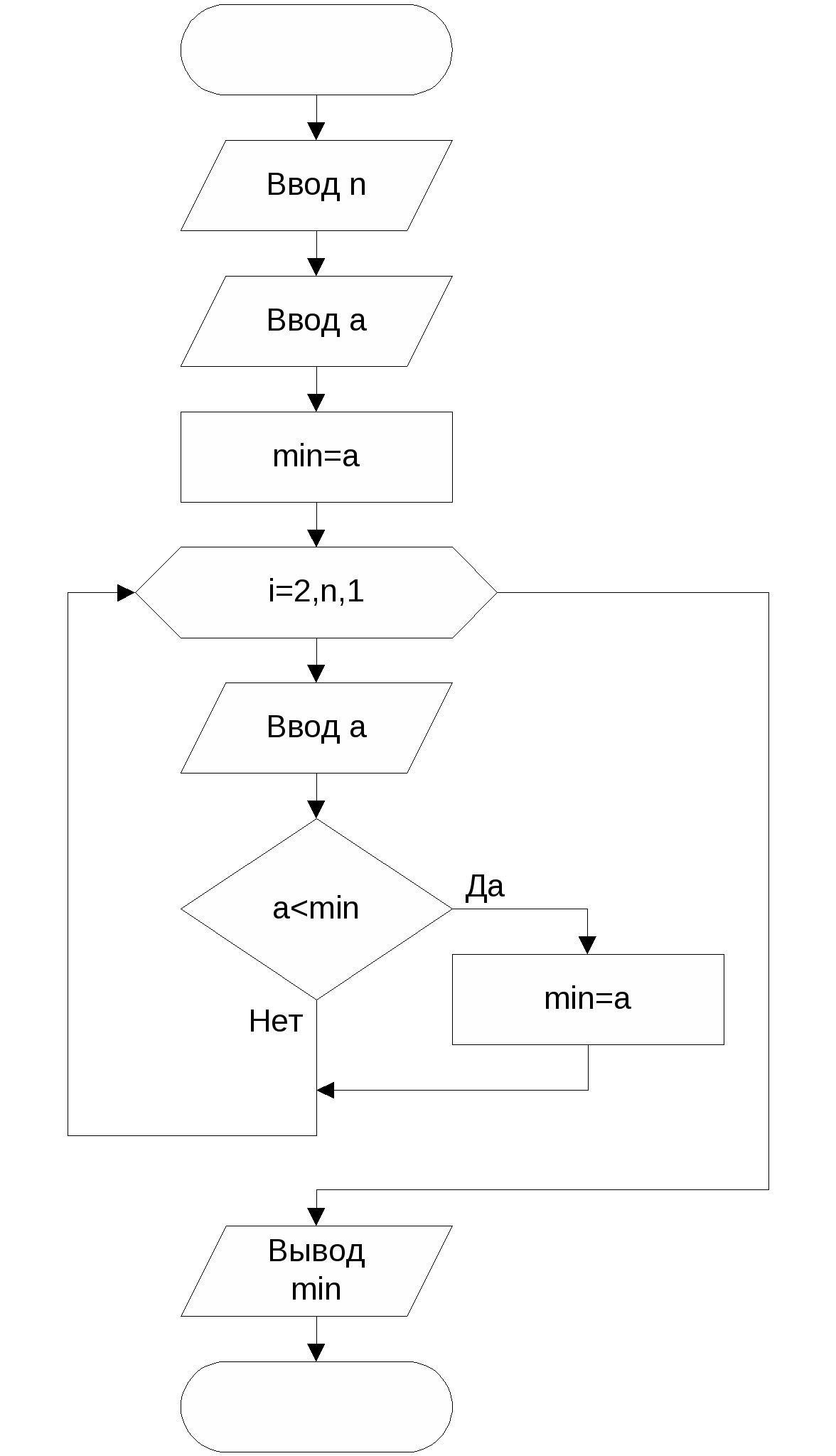 Тестовый пример: при n=7, последовательность: 8, 0, -1, 2, 10, 3, 5, min=-1. 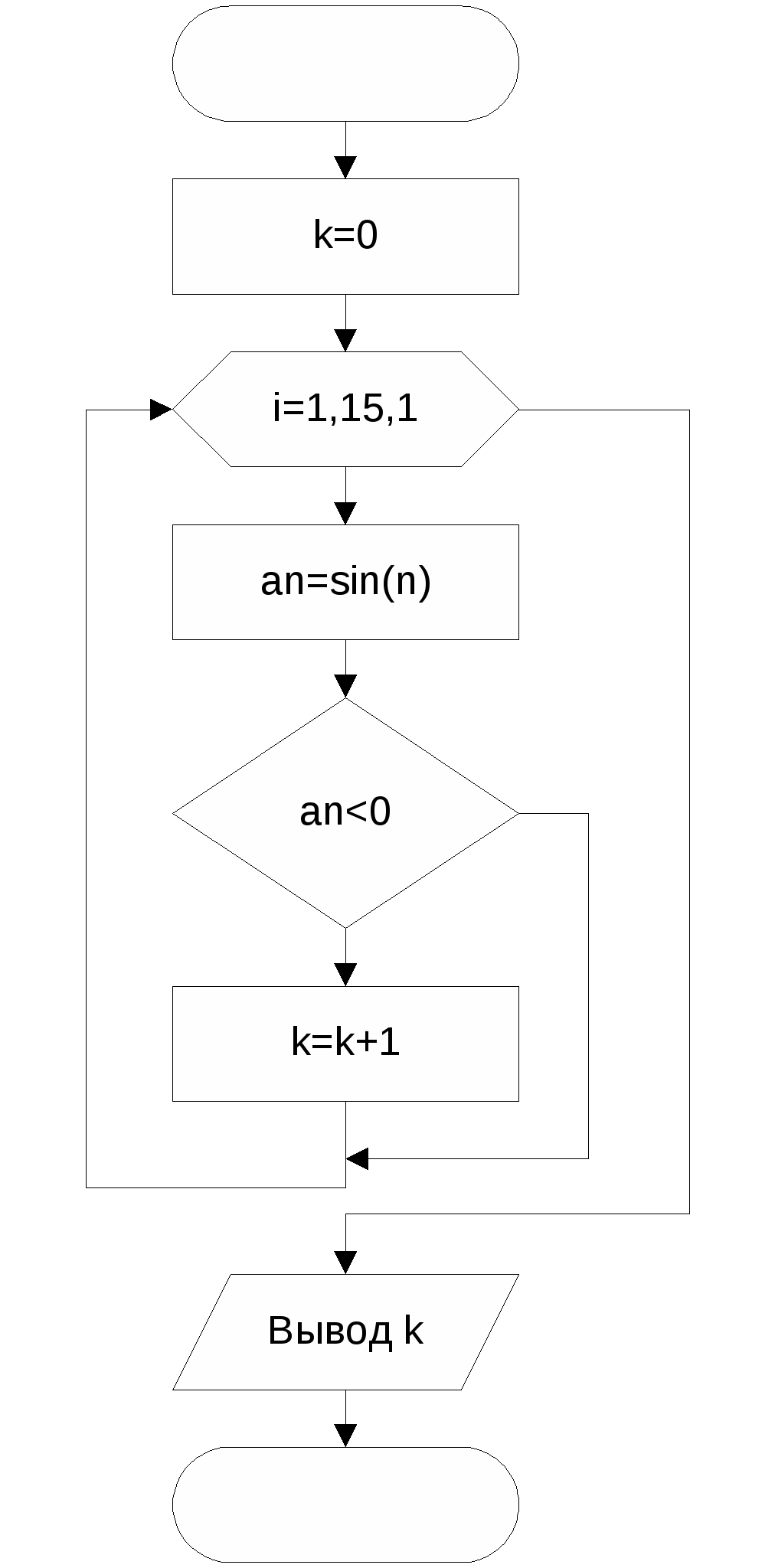 Дана числовая последовательность Исходные данные: количество элементов последовательности – 15. Результат: количество отрицательных элементов k – целый тип. Для нахождения количества отрицательных членов необходимо вычислить член последовательности и сравнить его с 0, если член меньше 0 увеличить k на единицу. В начале задачи k необходимо обнулить. Тестовый пример: С помощью Excel получаем k=6. Рассмотренные алгоритмы относятся к так называемым стандартным алгоритмам. Отметим. что у всех этих алгоритмов много общего. Рассмотрим следующую таблицу:
Вычислить факториал k. Факториалом называется произведение k!=123…k. Исходные данные: k – целый тип. Результат: fact – тип long int. Факториал числа очень быстро растет. Поэтому результат должен иметь длинный целый тип. Тестовый пример: При k=5, fact=120. 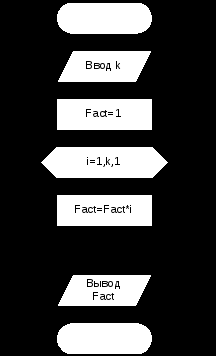 Даны натуральное число n, символы s1, …, sn. Известно, что среди s1, …, sn есть по крайней мере одна запятая. Найти такое натуральное i, что si – первая по порядку запятая; Исходные данные: Количество элементов n целое число, s – вводимый символ. Результат: k – номер первой запятой. Тестовый пример: при n=10 и последовательности ‘4hgj,e,6+,’ k=5. 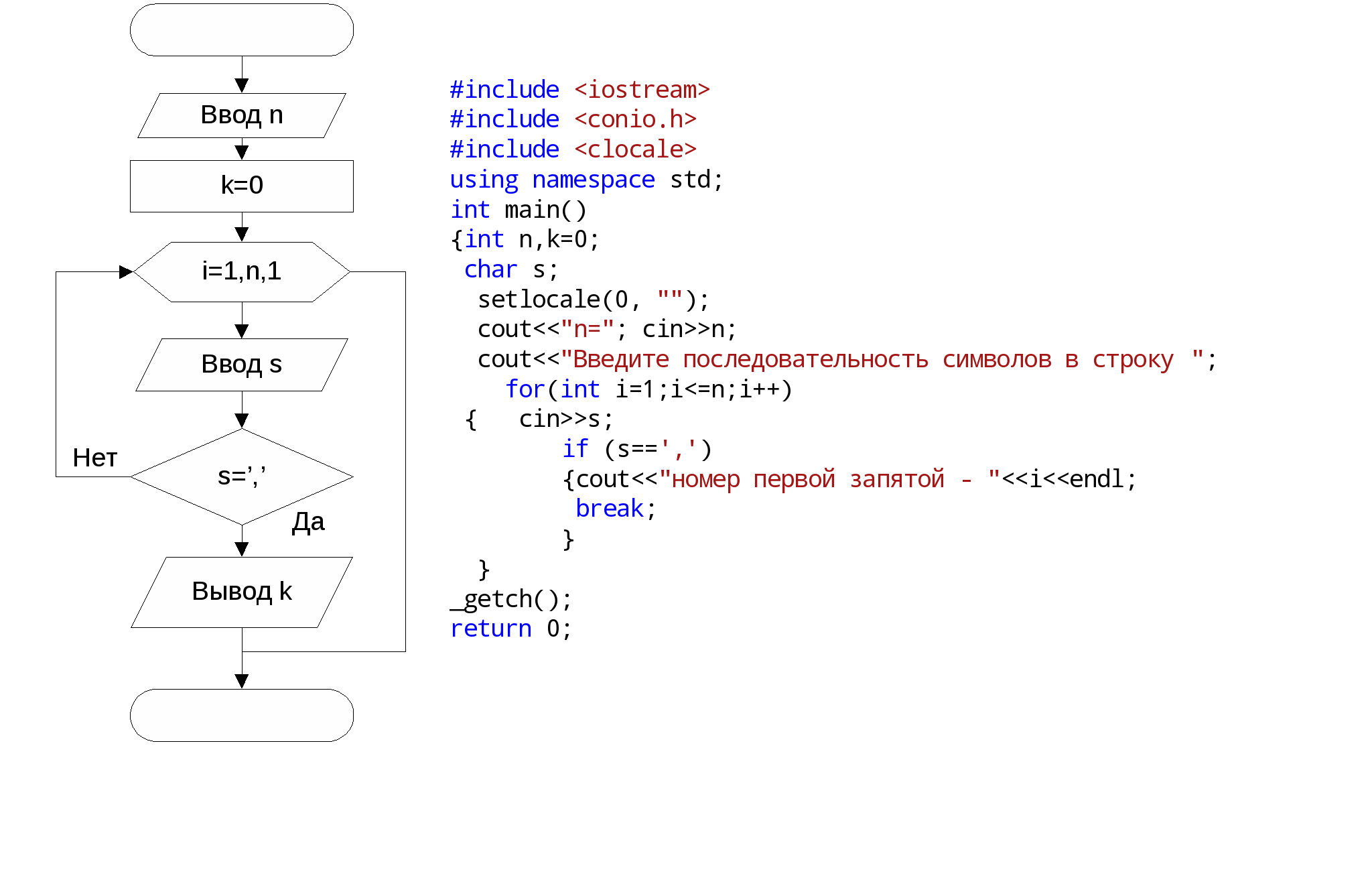 Во многих задачах требуется выполнять вычисления над элементами числовой последовательности, в которой каждый член an является функцией натурального аргумента n. В примере 6 приведен вариант такой последовательности. Часто по элементам числовой последовательности требуется определить формулу для вычисления n-го элемента. Д  ана числовая последовательность {a1=2, a2=5, a3=8, …}. Члены последовательности с четными номерами заменили на обратные им числа (5 на -5). Найти сумму членов последовательности с десятого по тридцать первый включительно. ана числовая последовательность {a1=2, a2=5, a3=8, …}. Члены последовательности с четными номерами заменили на обратные им числа (5 на -5). Найти сумму членов последовательности с десятого по тридцать первый включительно.Исходные данные: начальный член последовательности 10, конечный член последовательности – 31. Результат: Сумма членов последовательности s – целый тип. Необходимо определить формулу для вычисления члена последовательности в зависимости от номера члена. С увеличением номера на 1 член последовательности изменяется на 3, т.е. член зависит от 3*n. При n=1 элемент равен 2. Чтобы получить 2 необходимо из 3*n вычесть 1. Таким образом an=3*n-1. Чтобы определить четность номера достаточно найти остаток от деления номера на 2. Если остаток равен 0, то номер четный. Тестовый пример: с помощью Excel получаем s=-33 С 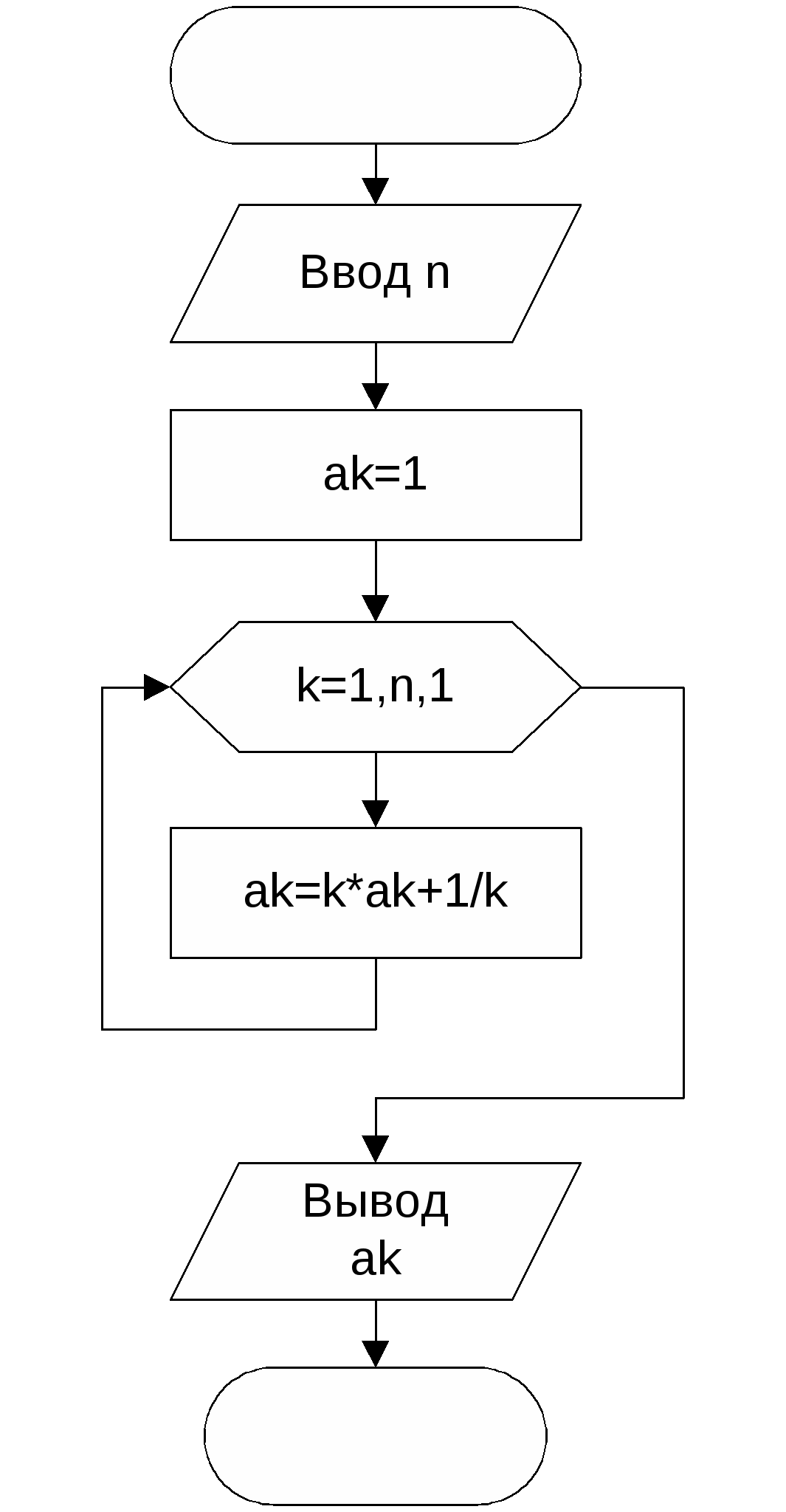 уществуют числовые последовательности, в которых каждый новый член вычисляется через предыдущие. Формула, в которой каждый член последовательности вычисляется через предыдущие, называется рекуррентной. Рекуррентная формула, если она существует, позволяет вычислить любой член последовательности посредством вычисления всех предыдущих членов. уществуют числовые последовательности, в которых каждый новый член вычисляется через предыдущие. Формула, в которой каждый член последовательности вычисляется через предыдущие, называется рекуррентной. Рекуррентная формула, если она существует, позволяет вычислить любой член последовательности посредством вычисления всех предыдущих членов.Пусть a0=1; ak=kak-1+1/k, k=1,2,… . Дано натуральное число n. Получить an. Исходные данные: номер элемента n - целый тип. Результат: n-й элемент последовательности а – вещественный тип. Тестовый пример: с помощью Excel получаем при n=5, an =278.12. Рассмотрим пример более сложной рекуррентной формулы Дана числовая последовательность: {a1=0, a2=4, …, an=an-1-3an-2}. Найти сумму отрицательных элементов при n=25. Исходные данные: количество элементов n - целый тип, значение х - an-2 целый тип, y - an-1 целый тип. Результат: Сумма отрицательных элементов S – целый тип. Для вычисления нового значения an необходимо знать 2 предыдущих значения. Для получения нового значения an надо знать an-1 и an-2 , которые необходимо сохранять в дополнительных переменных. Тестовый пример: с помощью Excel получаем S= -1644128 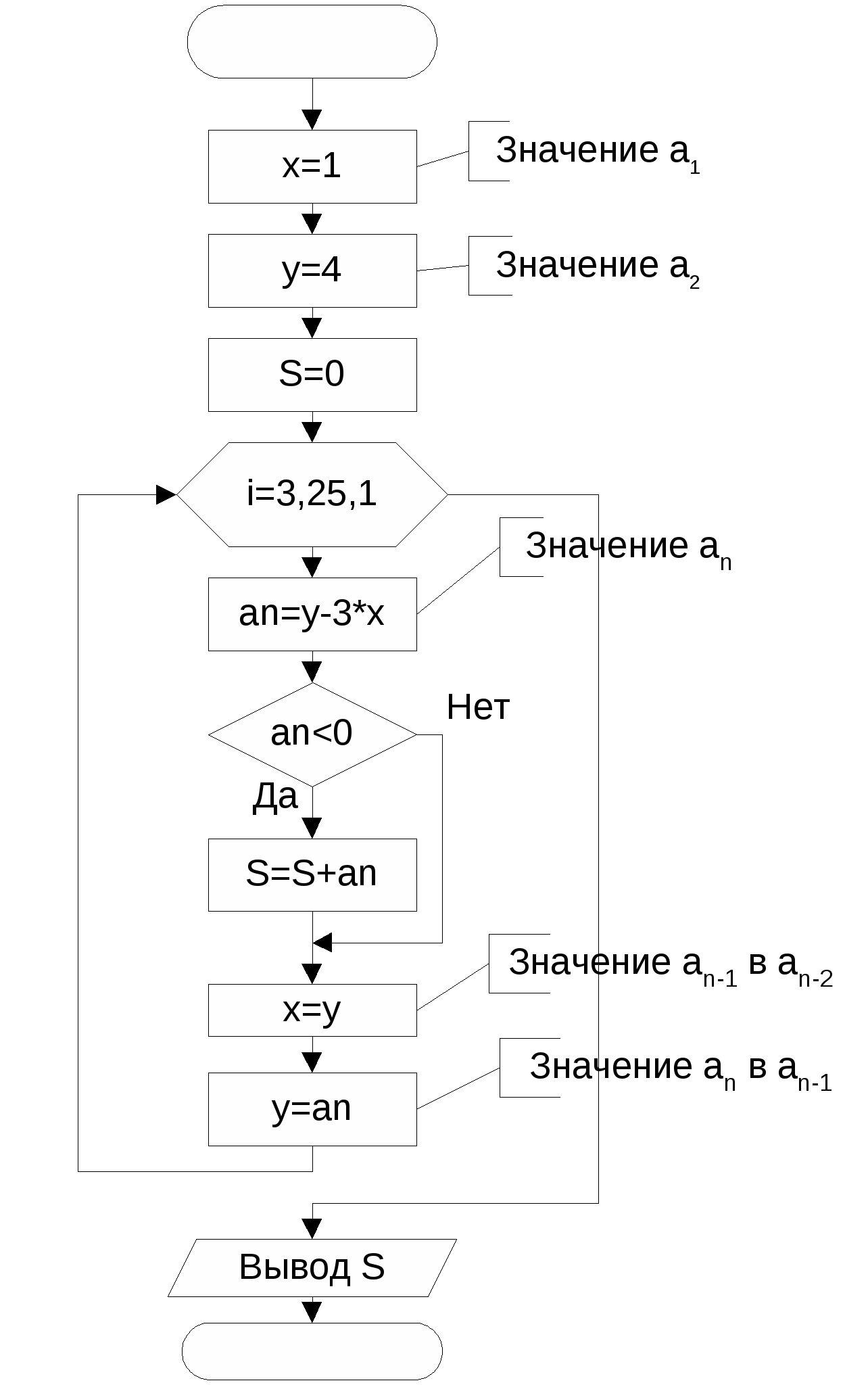  Даны натуральное число n, символы s1, …, sn. Выяснить, имеются ли в последовательности s1, …, sn такие члены последовательности, что si и si+1 совпадает с буквой t. Исходные данные: Количество элементов n целое число, s – вводимый символ. Результат: k – количество пар, равных t. Для сравнения пар введенных символов необходимо сохранять предыдущий введенный символ в переменной а. Тестовый пример: при n=15 в последовательности ‘ertbyttbnvttvcd’ k=2. Дано натуральное число n. Определить, сколько у этого числа делителей (1 и само число не учитывать). Исходные данные: n – целый тип. Результат: количество делителей k- целый тип. Тестовый пример: при n=24, k=6.  Даны натуральное число n, символы. s1, …, sn Подсчитать наибольшее количество идущих подряд запятых. Исходные данные: натуральное число n, вводимые символы s. Результат: Максимальное количество пробелов max целый тип. Если введенный символ равен ‘,’ надо увеличивать количество запятых идущих подряд на 1 (k). Если символ не запятая, надо проверить k, если символ следует сразу же после запятой (k>0) надо сравнить k с максимальным количеством запятых на данный момент. Если k>max, надо изменить значения max. После сравнения надо обнулить k перед поиском количества в новой серии запятых. Тестовый пример: при n=20, последовательность ’23,,wer,,,,,tyu,,,cv’, max=5. 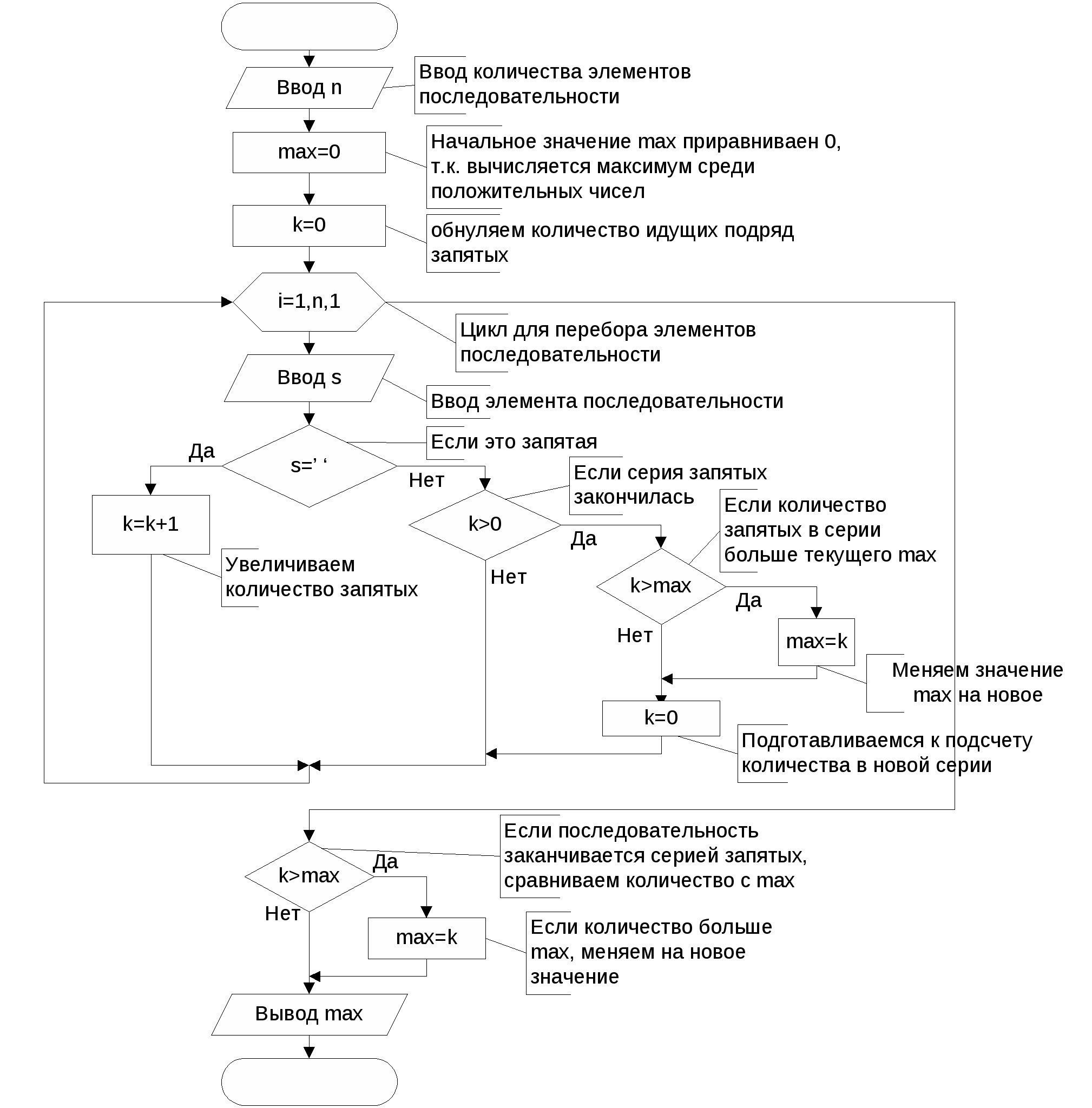 Задание 1 Написать программу и отладить Пример 11 и 13 Контрольные вопросы
Индивидуальные задания
,
Max(|z1|, |z2|, …, |zn|), где 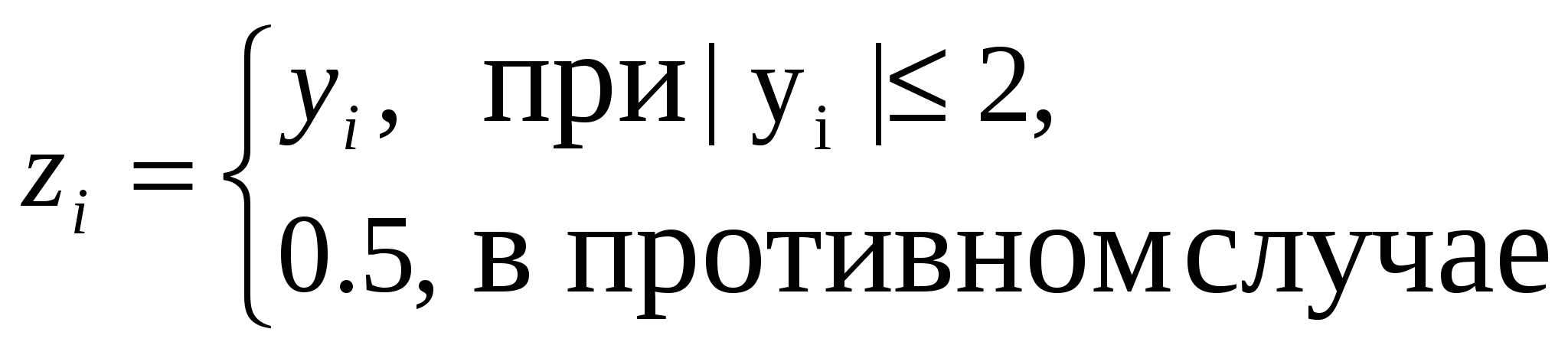
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

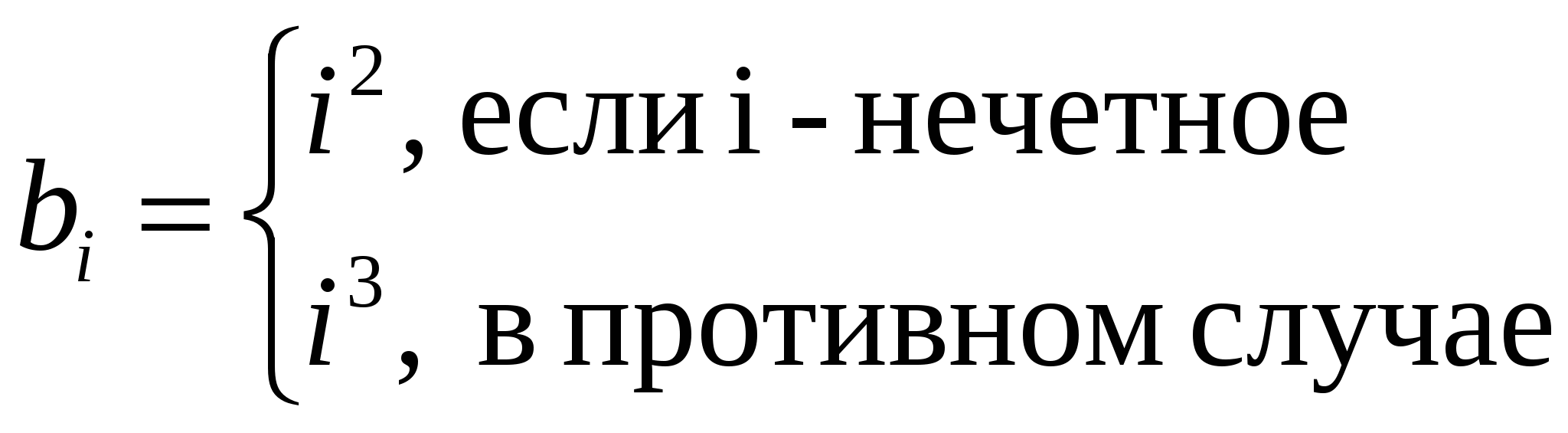
 ычислить , где
ычислить , где