Графы, матрицы и вес. Тема Использование информационных моделей (таблицы, диаграммы, графики)
 Скачать 2.64 Mb. Скачать 2.64 Mb.
|
Ещё пример задания:Р-04. Между населёнными пунктами A, B, C, D, E, F, G построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути между пунктами A и G (при условии, что передвигаться можно только по построенным дорогам). Решение: начнём строить возможные маршруты из пункта A; за 1 шаг можно приехать в B, D или сразу в G (в скобках показаны длины маршрутов): AB(5), AD(12), AG(25) заметим, что G – это целевая точка (конечный пункт), поэтому мы уже имеем один полный маршрут длиной 25 строим двух шаговые маршруты: из B дальше можно ехать в D (возврат в А неинтересен!) ABD (5 + 8 = 13) этот маршрут нет смысла продолжать, поскольку в D можно приехать быстрее: длина уже найденного маршрута AD равна 12 из D можно ехать в B и C: ADB (12 + 8 = 20) ADC (12 + 2 = 14) третий шаг: маршрут ADB продолжать бессмысленно: из B можно вернуться только в A и D продолжаем маршрут ADC (14): ADCE (14 + 4 = 18) ADCF (14 + 5 = 19) ADCG (14 + 10 = 24) в последнем варианте мы приехали в конечный пункт, причем новый маршрут имеет длину 24 < 25, то есть, он короче найденного ранее четвёртый шаг: продолжаем маршрут ADCE: ADCEG (18 + 5 = 23) и маршрут ADCF: ADCFG (19 + 5 = 24) других продолжений (без возврата в уже посещённые пункты) нет, поэтому кратчайший маршрут – ADCEG, он имеет длину 23. Ответ: 23. Заметим, что эти рассуждения можно зарисовать в виде дерева возможных маршрутов. После первого шага: 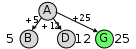 После второго шага:  После третьего шага: 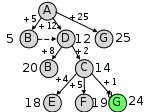 После четвёртого шага: 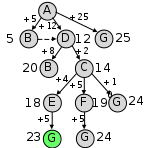 |
