Графы, матрицы и вес. Тема Использование информационных моделей (таблицы, диаграммы, графики)

• Название: Тема Использование информационных моделей (таблицы, диаграммы, графики)
• Дата: 27.09.2022
• Размер: 2.64 Mb.
• Имя файла: Графы, матрицы и вес.doc
• Тип: Документы; #699798
• страница: 3 из 14

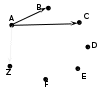
Ещё пример задания:

Р-05. Между населёнными пунктами A, B, C, D, E, F, Z построены дороги с односторонним движением. В таблице указана протяжённость каждой дороги. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет. Например, из A в B есть дорога длиной 4 км, а из B в A дороги нет.

	A	B	C	D	E	F	Z
A		4	6				30
B			3
C				11			27
D					4	7	10
E						4	8
F					5		2
Z	29

Сколько существует таких маршрутов из A в Z, которые проходят через 6 и более населенных пунктов? Пункты A и Z при подсчете учитывать. Два раза проходить через один пункт нельзя.

Решение (1 способ, перебор вариантов):

1. 
   обратим внимание, что числа в таблице нас совсем не интересуют – достаточно знать, что между данными пунктами есть дорога
   
2. 
   нам нужно найти все пути, которые проходят через 6 и более пунктов, считая начальный и конечный; то есть между A и Z должно быть не менее 4 промежуточных пункта
   
3. 
   начнем с перечисления всех маршрутов из А, которые проходят через 2 пункта; по таблице видим, что из A можно ехать в B, C и Z; количество пунктов на маршруте будем записывать сверху:
   

   2	3	4	5	6	7
   AB
   AC
   AZ

4. 
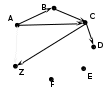
   маршрут AZ нас не интересует, хотя он и пришел в конечный пункт, он проходит меньше, чем через 6 пунктов (только через 2!); здесь и далее такие «неинтересные» маршруты из A в Z будем выделять серым фоном
   
5. 
   теперь ищем все маршруты, проходящие через 3 пункта; из B можно ехать только в C, а из С – в D и Z:
   

   2	3	4	5	6	7
   AB	ABC
   AC	ACD
   	ACZ
   AZ

6. 
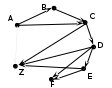
   далее из C едем в D и Z, а из D – в E, F и Z:
   

   2	3	4	5	6	7
   AB	ABC	ABCD
   		ABCZ
   AC	ACD	ACDE
   		ACDF
   		ACDZ
   	ACZ
   AZ

7. 
   строим следующий уровень только для тех маршрутов, которые ещё не пришли в Z:
   

   2	3	4	5	6	7
   AB	ABC	ABCD	ABCDE
   			ABCDF
   			ABCDZ
   		ABCZ
   AC	ACD	ACDE	ACDEF
   			ACDEZ
   		ACDF	ACDFE
   			ACDFZ
   		ACDZ
   	ACZ
   AZ

8. 
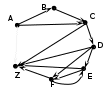
   следущие два уровня дают «интересные» маршруты, проходящие через 6 или 7 пунктов:
   

2	3	4	5	6	7
AB	ABC	ABCD	ABCDE	ABCDEF	ABCDEFZ
				ABCDEZ
			ABCDF	ABCDFE	ABCDFEZ
				ABCDFZ
			ABCDZ
		ABCZ
AC	ACD	ACDE	ACDEF	ACDEFE
				ACDEFZ
			ACDEZ
		ACDF	ACDFE	ACDFEF
				ACDFEZ
			ACDFZ
		ACDZ
	ACZ
AZ

9. 
   на последней схеме зелёным фоном выделены «интересные» маршруты, их всего 6; красным фоном отмечены маршруты, в которых получился цикл – они дважды проходят через один и тот же пункт; такие маршруты запрещены и мы далее их не рассматриваем
   
10. 
    Ответ: 6.
    
11. 
    можно было нарисовать схему возможных маршрутов в виде дерева: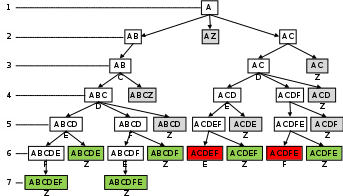
    

Решение (2 способ, через построение графа, М.В. Кузнецова)

1. 
   Построим граф, соответствующий таблице. Наличие значений преимущественно на диагонали таблицы говорит о наличии дорог, последовательно связывающих указанные населенные пункты (A-B, B-C, …). Построение графа начнем с размещения узлов (населенных пунктов), располагая их «по кругу», а затем последовательно изобразим все указанные в таблице дороги. Так как нас интересует только число дорог, проходящих через 6 и более пунктов, то длины дорог (веса ребер) указывать не будем.
   

   Из А исходит три дороги, но ясно, что дорога A-Z нас не интересует.	Из B исходит одна дорога, из С - две…
   Из D исходит три дороги, из Е – две.	Из F выходят две дороги, причём одна возвращает в Е (рисуем новую стрелку, FE и EF – разные дороги).

2. 
   Анализ графа.
   

Общее число пунктов 7. Есть дороги, последовательно связывающие все 7 пунктов, значит 1-й путь: ABCDEFZ.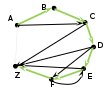



Есть 3 дороги, которые позволяют «проехать мимо» соседнего пункта (AC идёт «мимо» B, DF – мимо E,…), значит, есть 3 способа проехать через 6 пунктов (ACDEFZ, ABCDFZ, ABCDEZ).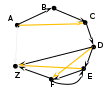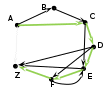

…
Есть одна «обратная дорога», позволяющая изменить порядок прохождения пунктов – FE. Эта дорога при наличии дороги DF, идущей «мимо» Е, создает дополнительные маршруты: один через 7 пунктов ABCDFEZ и один через 6 пунктов ACDFEZ.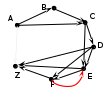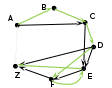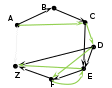

3. 
   Вывод: общее число дорог, соответствующих условию: 1+3+2=6
   
4. 
   Ответ: 6