Тема 1 Спецификация эконометрической модели Ошибки спецификации эконометрической модели имеют место вследствие
 Скачать 1.2 Mb. Скачать 1.2 Mb.
|
|
Тема 11: Проверка статистической значимости эконометрической модели 1. При расчете скорректированного коэффициента множественной детерминации пользуются формулой 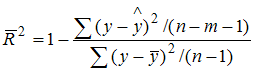 , где … , где …n – число наблюдений; m – число факторов, включенных в модель множественной регрессии 2. Если известно уравнение множественной регрессии 766,67 3. Для регрессионной модели известны следующие величины дисперсий: Тема 12: Оценка значимости параметров эконометрической модели 1. Для уравнения множественной регрессии вида При уровне значимости 0,1 значимыми являются параметры … 2. Если для среднеквадратической ошибки параметра и значения оценки этого параметра линейной эконометрической модели выполняется соотношение , то это свидетельствует о статистической ______ параметра. ненадежности оценки 3. Для уравнения множественной регрессии вида Для данного уравнения при уровне значимости α=0,05 значимыми являются параметры … 4. Проверка статистически значимого отличия от нуля оценок коэффициентов осуществляется путем последовательного сравнения отношений ( –среднеквадратическая ошибка параметра ) с точкой, имеющей распределение … Стьюдента Тема 13: Нелинейные зависимости в экономике 1. Если зависимость объема спроса от цены характеризуется постоянной эластичностью, то моделирование целесообразно проводить на основе … степенной функции 2. Если по результатам анализа поля корреляции замечено, что на интервале изменения фактора меняется характер связи рассматриваемых признаков, прямая связь изменяется на обратную, то моделирование целесообразно проводить на основе … параболы второй степени 3. Нелинейное уравнение регрессии вида полиномиальной … парной 4. Если с увеличением масштабов производства удельный расход сырья сокращается, то моделирование целесообразно проводить на основе … равносторонней гиперболы Тема 14: Виды нелинейных уравнений регрессии 1. Степенной моделью не является регрессионная модель … 2. Среди предложенных нелинейных зависимостей нелинейной по параметрам является … 3. Среди предложенных нелинейных зависимостей нелинейной существенно (внутренне нелинейной) является … 4. Среди предложенных нелинейных зависимостей внутренне линейной является … Тема 15: Линеаризация нелинейных моделей регрессии 1. Для линеаризации нелинейной регрессионной модели используется … логарифмирование 2. Для преобразования внутренне нелинейной функции может быть применен метод … разложения функции в ряд Тейлора 3. Для линеаризации нелинейной функции может быть применен метод … логарифмирования и замены переменных Тема 16: Оценка качества нелинейных уравнений регрессии 1. При расчете уравнения нелинейной регрессии [0,8; 1] 2. По 20 регионам страны изучалась зависимость уровня безработицы y (%) от индекса потребительских цен x (% к предыдущему году) и построено уравнение в логарифмах исходных показателей: 0,64 3. Для регрессионной модели , где – нелинейная функция, – рассчитанное по модели значение переменной , получены значения дисперсий: 0,096 4. Для регрессионной модели , где – нелинейная функция, – рассчитанное по модели значение переменной , получено значение индекса корреляции R = 0,64. Моделью объяснена часть дисперсии переменной , равная … 5. По результатам проведения исследования торговых точек было построено уравнение нелинейной регрессии при уровне значимости можно считать, что эластичность спроса по цене составляет –0,8 Тема 17: Временные ряды данных: характеристики и общие понятия 1. В состав любого временного ряда, построенного по реальным данным, обязательно входит _____ компонента. случайная . 2. Ряд, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, изображен на графике … 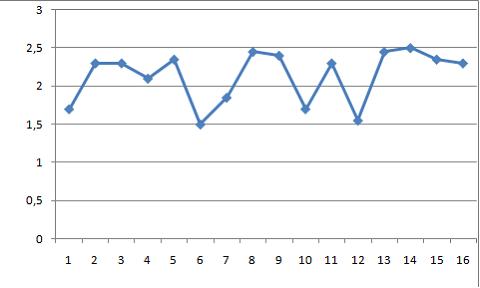 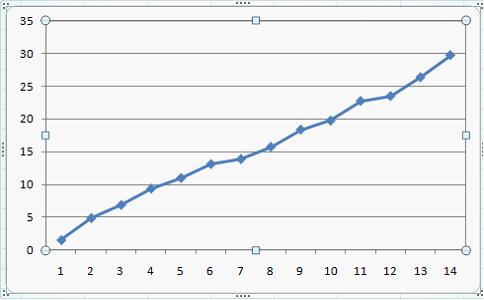 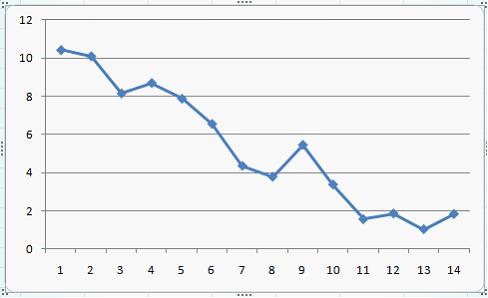 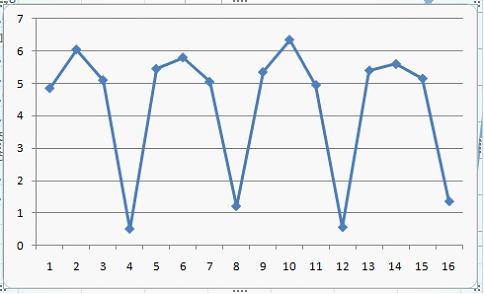 Решение: График ряда, уровни которого образуются как сумма среднего уровня ряда и некоторой случайной компоненты, будет колебаться относительно своего среднего значения. 3. Совокупность значений экономического показателя за несколько последовательных моментов (периодов) времени называется … временным рядом 4. Выраженную положительную тенденцию содержит ряд …  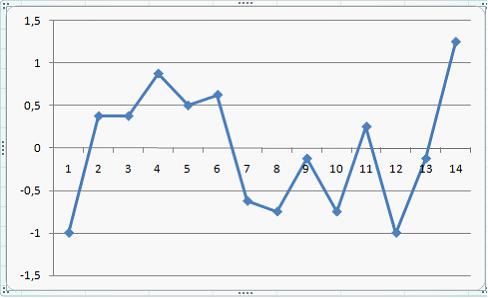 - -  Решение: Ряд имеет выраженную положительную тенденцию, если уровни ряда увеличиваются с увеличением периода времени t. Тема 18: Структура временного ряда 1. Значение коэффициента автокорреляции первого порядка характеризует … тесноту линейной связи 2. Дана автокорреляционная функция временного ряда  Верным будет утверждение, что ряд … Верным будет утверждение, что ряд …имеет выраженную сезонную компоненту с лагом 4 3. Автокорреляционной функцией временного ряда называется последовательность коэффициентов автокорреляции … первого, второго, третьего и последующих порядков 4. Значение коэффициента автокорреляции второго порядка равно (-0,6), следовательно, ряд содержит … тенденцию 5. Автокорреляцией уровней ряда называется корреляционная зависимость между … последовательными уровнями ряда Тема 19: Аддитивная и мультипликативная модели временных рядов 1. Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Для аддитивной модели временного ряда для уровня y3 получено уравнение тренда T = 3,14 + 2,07t. Известны значения компонент: S3 = 1,6; E3 = –0,3. Тогда значение уровня временного ряда y3 будет равно … 10,65 2. Уровень временного ряда (yt) формируется под воздействием различных факторов – компонент: Т (тенденция), S (циклические и/или сезонные колебания), Е (случайные факторы). Для мультипликативной модели временного ряда, содержащего периодические колебания в 4 момента, получены значения сезонных компонент: S1 = 2,087; S2 = 0,632; S3 = 0,931; S4 = 3,256. Известны значения компонент: T5 = 20,6 и E5 = 0,4. Рассчитайте значение уровня временного ряда y5. 17,2 3. Для аддитивной модели временного ряда Y = T + S + E лаг модели равен 4 и известны значения трех скорректированных сезонных компонент: , , . равна … 1 4. Для мультипликативной модели временного ряда Y = T · S · E сумма скорректированных сезонных компонент равна … лагу Тема 20: Модели стационарных и нестационарных временных рядов и их идентификация 1. Известно, что дисперсия временного ряда Y увеличивается с течением времени. Значит, ряд Y … нестационарным 2. Известно, что временной ряд Y порожден случайным процессом, который по своим характеристикам является «белым шумом». Значит, ряд Y … стационарный 3. Известно, что временной ряд Y характеризуется устойчивой тенденцией, то есть его среднее значение меняется. Значит, ряд Y, скорее всего,является … нестационарным 4. Для временного ряда известны характеристики: – среднее и – дисперсия. Если временной ряд является стационарным, то … Тема 21: Общие понятия о системах уравнений, используемых в эконометрике 1. Левая часть системы эконометрических уравнений представлена совокупностью _________ переменных. зависимых эндогенных 2. Модель равенства спроса и предложения, где предложение и спрос являются линейными функциями цены p, состоит из уравнений … 3. Системой эконометрических уравнений не является система линейных _____ уравнений. стандартизованных Тема 22: Классификация систем уравнений 1. При построении систем эконометрических уравнений различают три класса моделей: (1) система независимых уравнений; (2) система рекурсивных уравнений; (3) система одновременных уравнений. Отнесите предложенные модели к соответствующему классу. 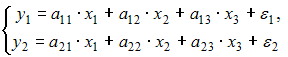 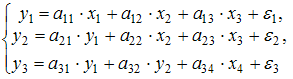 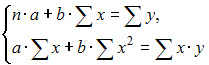 Решение: Модель, в которой – продуктивность коров, можно назвать моделью экономической эффективности сельскохозяйственного производства. Эта модель содержит в правой части только независимые переменные, поэтому она может быть отнесена к классу «система независимых уравнений». Модель, в которой – производительность труда, может быть названа моделью производительности труда и фондоотдачи. Это модель содержит в первом уравнении только независимые переменные, а во втором уравнении в правой части встречается и зависимая переменная ; это значит, что модель можно отнести к классу «система рекурсивных уравнений». Модель, в которой – темп изменения месячной заработной платы, может служить моделью динамики цены и заработной платы. В правых частях обоих уравнений содержатся зависимые переменные, поэтому данная модель может быть отнесена к классу «система одновременных уравнений». Система, в которой y – объем производства, вообще не является какой бы то ни было системой эконометрических уравнений – это система нормальных уравнений для определения параметров парной линейной регрессии. 2. Изучаются модели зависимости спроса и предложения от цены p и прочих факторов. Установите соответствие между видом и классом эконометрических уравнений. (1) 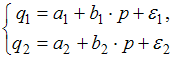 (2) 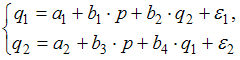 (3) 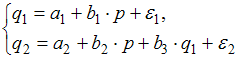 система независимых уравнений 1 система одновременных уравнений 2 система рекурсивных уравнений 3 3. Установите соответствие между видом и классом эконометрических уравнений. (1) 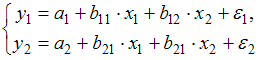 (2) (3) система независимых уравнений 1 система рекурсивных уравнений 2 система одновременных уравнений 3 система нормальных уравнений 4. Установите соответствие между видом и классом системы эконометрических уравнений: (1) 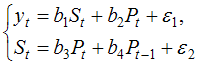 (2) 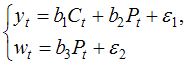 система одновременных уравнений с лаговыми переменными 1 система независимых уравнений 2 система одновременных уравнений без лаговых переменных 5. Установите соответствие между классом и видом системы эконометрических уравнений: (1) система одновременных уравнений (2) система рекурсивных уравнений (3) система независимых уравнений 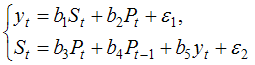 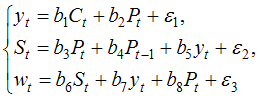 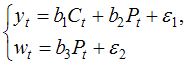 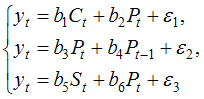 |
