Методичка стат. Стат. Тема 2. Статистическое наблюдение 1
 Скачать 143.52 Kb. Скачать 143.52 Kb.
|
|
Тема №1. «Предмет и метод статистической науки» 1 Тема №2. «Статистическое наблюдение» 1 Тема №3. «Сводка и группировка статистических данных» 2 Тема №4. «Статистические показатели» 3 Тема №5. «Средние величины» 4 Тема №6. «Показатели вариации» 10 Тема №7. «Выборочное наблюдение» 10 Тема №8. «Статистические методы анализа корреляционных связей» 12 Тема №9. «Ряды динамики» 13 Тема №10. «Экономические индексы 15 Тема №1. «Предмет и метод статистической науки» Социально-экономическая статистика – изучает количественную сторону различных массовых экономических и социальных явлений и процессов общественной жизни с учётом их качественной стороны. При этом изучение осуществляется при помощи системы статистических показателей, экономических и социальных явлений, а также экономики народного хозяйства в целом. Отраслевая статистика – осуществляет статистическое изучение отдельных отраслей общественного производства. Тема №2 «Статистическое наблюдение» Статистическое наблюдение – это сбор сведений, заключающийся в регистрации (учете) признаков и фактов, которые характеризуют каждую единицу исследуемой (изучаемой) совокупности. Данные о каждой единице наблюдения являются результатом статистического учета и представляют собой первичную информацию. В результате статистического наблюдения образуется совокупность первичной информации. Статистическое наблюдение должно представлять собой планомерную, систематическую и научно обоснованную работу по сбору массовых данных о явлениях и процессах социально-экономической жизни путем регистрации существенных признаков по заранее разработанной программе. Планомерность статистического наблюдения заключается в том, что оно готовиться по специально разработанному плану и проводится в несколько этапов: • организационно-подготовительные работы, • непосредственный сбор первичных данных, • контроль собранной информации. Системность предполагает, что программа статистического наблюдения входит в программу всего статистического исследования и включает вопросы методологии, организации, техники сбора информации, контроля ее достоверности и оформления итоговых результатов. Научная обоснованность обязывает исследователей подробно изучить объект с точки зрения качеств, свойств и признаков, характеризующих объект; провести экспериментальные расчеты и пробные обследования; разработать новую или подобрать готовую методику проведения статистического наблюдения. Разработка программы наблюдения требует коллективных усилий многих специалистов соответствующих отраслей знаний. Разработка программы наблюдения охватывает следующие программно-методологические вопросы: • постановку цели и задач наблюдения, • определение объекта наблюдения и его границ, • установление единицы наблюдения и отчетной единицы, 2 • составление перечня признаков, характеризующих единицу наблюдения, • выбор методов, видов, форм и способов организации наблюдения. Цель обследования определяет все последующие этапы и действия по проведении статистического наблюдения. Цель определяется исходя из основных гипотез и предполагаемых результатов проводимого исследования. Конкретные задачи исследования определяют те сведения, которые должны быть получены в процессе наблюдения. Тема №3 «Сводка и группировка статистических данных» При изучении понятия группировки следует особо обратить внимание на виды группировочных признаков: они могут быть количественные и качественные (атрибутивные). Количественный признак выражается только в числовом виде, а качественный или атрибутивный выражается вербально, то есть в виде слов и терминов. Такая трактовка группировочных признаков характерна только для статистической сводки и группировки, в других темах, например, «Индексы» данные понятия могут иметь другое содержание. Группировки, выполненные по атрибутивному или качественному признаку, часто называют классификациями или номенклатурой. Как правило, такие группировки часто оформляются в виде классификаторов, создаются статистическими органами и носят характер статистических стандартов. Классификатор представляет собой массив информации, где каждому значению группровочного признака присвоен код, то есть условное цифровое обозначение. Имеется достаточно много классификаторов имеющих силу общероссийских стандартов. Самым распространенным является общероссийский классификатор продукции ОКП. Данный классификатор содержит около 50 тыс. видов продукции по такой иерархии; класс, подкласс, группа, подгруппа, вид. Тема №4 «Статистические показатели» Абсолютные величины — это именованные числа и в зависимости от характера явления или процесса могут иметь разные единицы измерения: натуральные (кг, м, шт. и т.д.); условно-натуральные (одна условная банка консервов, одна условная единица минеральных удобрений и т. д.); Согласно инструкции Госкомстата №106 от 01.11.2000 года за условную банку принимается банка массой 400 г для овощных и фруктовых консервов. Для мясных консервов условной считается банка емкостью 440 г, для мясорастительных – 179 г, для рыбных консервов и консервов из морепродуктов – 350 г; для всех других видов консервов за учетную (условную) единицу принимается банка емкостью 353,4 куб. см. Условное топливо – принятая при расчетах единица учёта органического топлива, то есть нефти и ее производных, природного и специально получаемого при перегонке сланцев и каменного угля, газа, торфа – которая используется для счисления полезного действия различных видов топлива в их суммарном учёте. Основной показатель топлива – удельная теплота сгорания. Для целей сравнения видов топлива введено понятие условного топлива. В СССР и России за единицу условного топлива (у.т.) принималась теплотворная способность 1 кг каменного угля = 29,3 МДж или 7000 ккал. Топливо условное - единица учёта органического топлива, применяемая для сопоставления эффективности различных видов топлива и суммарного учёта их. В качестве единицы т. у. принимается 1 кг топлива с теплотой сгорания 7000 ккал/кг (29,3 Мдж/кг). Соотношение между т. у. и натуральным топливом выражается формулой: 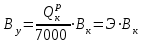 где By – масса эквивалентного количества условного топлива, кг; Вн – масса натурального топлива, кг (твёрдое и жидкое топливо) или м3(газообразное); 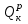 – низшая теплота сгорания данного натурального топлива, ккал/кг или ккал/м3; – низшая теплота сгорания данного натурального топлива, ккал/кг или ккал/м3; 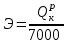 – калорийный эквивалент. – калорийный эквивалент.Пересчет количества топлива данного вида в условное производится с помощью коэффициента, равного отношению теплосодержания 1 кг топлива данного вида к теплосодержанию 1 кг условного топлива. Например, коэффициент пересчета 1 м3 газа горючего природного в 1 единицу условного топлива равен 1,14. Тогда 1 м3 будет эквивалентен 1,14∙7000=7980 ккал (33,4 мдж/м3) теплоты. В процессе изучения видов относительных показателей следует обратить внимание на то, что основной тип задач по этой теме предполагает определение к какому виду относится рассчитываемый в задаче показатель. Наибольшую трудность вызывают, как правило, идентификация относительных величин координации и относительных величин интенсивности. В данном случае следует обратить внимание на тот факт, что относительные величины координации дают соотношение разных структурных единиц самой совокупности и показывают, сколько единиц одной части совокупности приходится на 1, 100, 1000 и больше единиц другой, взятой за базу сравнения, то есть при расчете такого показателя и в числителе, и в знаменателе будут находится абсолютные величины, имеющие одну и туже единицу измерения. При расчете относительной величины интенсивности, котораяхарактеризуются отношением разноименных величин, связанных между собой определенным образом, находится отношение разноименных показателей, то есть абсолютные величины, используемые для расчета такого показателя, будут иметь различные единицы измерения. Тема №5 «Средние величины» При изучении данной темы необходимо обратить особое внимание на правильный выбор средней степенной. Для этой цели используется алгоритм выбора средней степенной, который состоит из следующих этапов: 1. Определить цели и задачи вычисления средней степенной величины. 2. Определить определяющий показатель и формулу его расчета. 3. Выбрать вид средней степенной величины исходя из правила: значение определяющего показателя не должно измениться при замене индивидуальных значений признака на среднее значение. Необходимо особо обратить внимание на тот факт, что пункт алгоритма «определить цели и задачи вычисления средней степенной величины» не является формальным и в зависимости от цели вычислений даже при одних и тех же условиях, но разных целях может получиться и разный вид средней степенной величины. Следует понимать, что средние степенные величины не исчерпываются приведенными в курсе величинами. Рассмотрим конкретный пример связанный с расчетом средних показателей на одном массиве данных, но при этом цели и задачи будут различны. Работа одного вида выполняется на n объектах. С целью контроля за расходом материалов рассмотрим задачу об определении среднего объема работ. Известно, что на i-ом объекте выполнен объем работ Qi и при этом израсходовано Miколичества материалов одного вида. Используя алгоритм выбора средней степенной получаем: В качестве определяющего показателя выберем общий расход материалов при выполнении объемов работ данного вида, на всех n объектах. Запишем формулу для расчета определяющего показателя 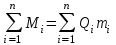 где mi – удельный расход материала на i-ом объекте (работе). Согласно алгоритма выбора средней степенной, значение определяющего показателя не будет изменяться при замене индивидуальных значений признака на среднее значение, то есть должно выполняться следующее соотношение 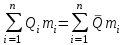 . .Величину не имеющую индекса суммирования, то есть 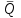 , можно вынести за знак суммирования, то есть выражение для определяющего показателя можно записать в следующем виде , можно вынести за знак суммирования, то есть выражение для определяющего показателя можно записать в следующем виде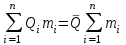 . .Отсюда находим средний объем работ по всем объектам 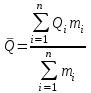 . .Но в данном выражении остается неизвестной величина удельного расхода материала mi на i-ом объекте (работе). Находим его 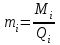 Подставляя найденное значение mi в выражение для расчета среднего объема работ, то есть 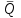 , получаем , получаем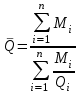 . .Таким образом, средний объем работ по совокупности n объектов вычисляется по средней гармонической взвешенной, в которой в качестве доли признака используется количество материала Mi, а в качестве осредняемого признака Qi. Рассмотрим теперь задачу об определении среднего удельного расхода материалов. Известно, что на i-ом объекте или работе, использующей один и тот же материал, израсходовано Miколичества материалов этого вида, при этом удельный расход материала составил mi. Работы данного вида выполняются на n объектах. В целях контроля за расходом материала необходимо вычислить среднее значение расхода материала данного вида на единицу работы, то есть удельный расход по всем объектам или работам. Используя алгоритм выбора средней степенной получаем: В качестве определяющего показателя выберем общий расход материалов данного вида на всех работах. Запишем формулу для расчета определяющего показателя 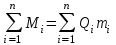 где mi – удельный расход материала на i-ом объекте (работе). Согласно алгоритма выбора средней степенной, значение определяющего показателя не будет изменяться при замене индивидуальных значений признака на среднее значение, то есть должно выполняться следующее соотношение 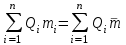 . .Величину не имеющую индекса суммирования, то есть 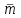 , можно вынести за знак суммирования, то есть выражение для определяющего показателя можно записать в следующем виде , можно вынести за знак суммирования, то есть выражение для определяющего показателя можно записать в следующем виде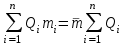 . .Отсюда находим средний удельный расход материалов по рассматриваемому виду работ 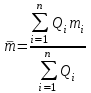 . .Но в данном выражении остается неизвестной величина объема выполненных работ Qi на i-ом объекте (работе). Находим его 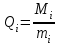 Подставляя найденное значение mi в выражение для расчета среднего удельного расхода то есть 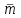 , получаем , получаем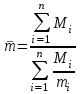 . .Таким образом, средний удельный расход материала вычисляется по средней гармонической взвешенной, в которой в качестве доли признака используется количество материала Mi, а осредняемым признаком является mi. Из всего спектра средних степенных особое место занимает средняя геометрическая, которуюприменяют в тех случаях, когда объем совокупности формируется не суммой, а произведением индивидуальных значений признаков. Этот вид средней используется для вычисления средних коэффициентов (темпов) роста в рядах динамики. Так, в случае одинаковых временных интервалов между и уровнями динамического ряда средняя геометрическая простая имеет такой вид: 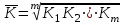 где 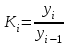 темпы роста; уi, уi-1 — соответственно текущий и предыдущий уровни ряда; т – количество темпов роста (т = п – 1). темпы роста; уi, уi-1 — соответственно текущий и предыдущий уровни ряда; т – количество темпов роста (т = п – 1).Если временные интервалы между и уровнями динамического ряда неравны, то используется средняя геометрическая взвешенная 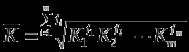 Подчеркнем особенности использования данной формулы: если исходный ряд динамики содержит n уровней ряда, то по этим данным можно вычислить темпы роста только за (n – 1) периодов. Таким образом, для базисного, как правило начального, уровня темп роста не вычисляется из-за недостаточности исходных данных. Это обстоятельство позволяет ряд динами условно разбить на две части: базисный период и изучаемый период (все уровни динамического ряда кроме первого). Обозначив число уровней ряда составляющих изучаемый период через m и приходим к приведенной выше формуле. Следует отметить, что данная формула расчета средних темпов роста в рядах динамики имеет достаточно существенный недостаток. Если в формулу простой средней геометрической подставить значения цепных темпов роста, то получим 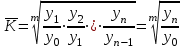 , ,то есть при вычислении среднего темпа роста используется только конечный и начальный уровень ряда динамики, влияние же остальных значений в данном случае учитываться не будет. Это обстоятельство послужило основой для того факта, что в теории статистики данный способ расчета средних темпов роста не считается универсальным, так как очень часто необходимо контролировать темпы роста по каждому периоду, что при подобном способе расчета сделать будет уже невозможно, так как использование среднего тепа роста, рассчитанного по данной формуле будет давать искаженный результат. Данный факт иллюстрирует следующий пример. Рассмотрим расчет темпов роста характеризующих динамику объемов работ (в млрд. рублей), выполненных собственными силами, по виду деятельности «Строительство», в Воронежском регионе за последние пять лет. Соответствующие данные приведены в табл. 1. Таблица 1.
Таким образом суммарный объем выполненных строительных работ за последние пять лет в Воронежском регионе составил 296,6 млрд. руб. Понятно, что данный динамический ряд делится на две расти: за базисный уровень приятны данные 2010 года, а изучаемый период составляет 4 года: 2011, 2012, 2013, 2014. Таким образом, в данной задаче m=4. Находим средний темп роста 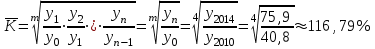 Теперь можно проверить, что уровень 2014 года может быть определен по формуле 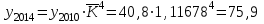 , ,и составляет фактическую величину, достигнутую в этом году. Однако, если использовать данное среднее значение темпа роста для других уровней динамического ряда, то получим следующее: 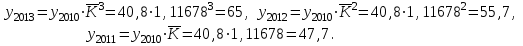 Теперь найдем общий объем произведенных работ в Воронежском регионе за последние пять лет с использованием полученного значения среднего темпа роста. Получим 75,9+65+55,7+47,7+40,8=285 млрд. руб. Таким образом отклонение фактического объема выполненных работ от объемов работ, полученных расчетным путем составляет 11,6 млрд. руб. или 3,9% от базисного периода за который принят 2010 год. Такое отклонение стало возможным из-за особенностей расчета среднего темпа роста, когда используются только два значения из всего рада динамики: первое и последнее. Попробуем применить алгоритм выбора средней степенной величины к данной задаче. 1. Определяем цель и задачи вычисления средней величины. Понятно, что в данном случае задача заключается в получении такой средней величины, которая максимально точно отражала бы данные об объеме выполненных работ как за весь анализируемый период, так и отдельно по годам. 2. Исходя из цели и задач выбираем определяющий показатель и формулу его расчета. В данном случае в качестве определяющего показателя принимается объем выполненных работ за весь анализируемый период, то есть 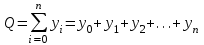 , ,или применительно к нашим исходным данным получаем 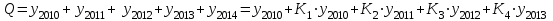 . .Учитывая формулу для расчета цепных темпов роста 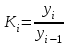 , получаем , получаем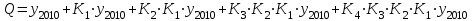 . .3. Выбираем вид средней степенной величины исходя из правила: значение определяющего показателя не должно измениться при замене индивидуальных значений признака на среднее значение. В этом случае последнее выражение преобразуется к виду: 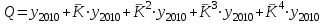 Преобразуя левую часть и приводя подобные получим 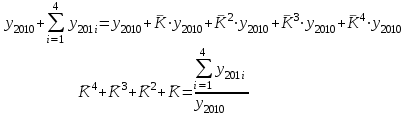 Таким образом, средняя величина темпа роста, удовлетворяющая поставленным условиям, будет находится из решения полученного линейного алгебраического уравнения четвертой степени. Для случая произвольного изучаемого периода, состоящего из n уровней ряда, соответствующее уравнение запишется в виде 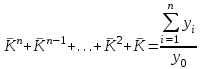 Средняя величина, найденная из данного соотношения, получила название средней параболической. Вполне понятно, что решить данное уравнение аналитически для произвольного случая невозможно, поэтому используются приближенные методы решения. Наибольшее распространение получила следующая форма средней параболической величины 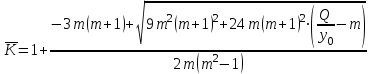 где m – число изучаемых периодов; 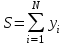 - сумма уровней изучаемого периода; y0 – базисный уровень, то есть период, предшествующий изучаемому. - сумма уровней изучаемого периода; y0 – базисный уровень, то есть период, предшествующий изучаемому.Отсюда средний темп прироста будет составлять 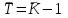 . .Учитывая, что средних величин достаточно много и они не совпадают даже для одной и той же совокупности, естественно возникает вопрос об их соотношении. Это задается правилом мажорантности средних 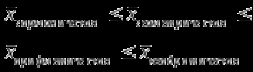 При изучении структурных (позиционных средних) необходимо обратить внимание на тот факт, что для совокупности будет характерным три квартили и девять децилей. Причем вторая квартиль и пятая дециль будут совпадать с медианой данной совокупности. Тема №6 «Показатели вариации» Основное внимание необходимо уделить понятию вариации совокупности и способом ее количественного описания. Показать, что дисперсия имеет основной недостаток, который заключается в том, что единицы ее измерения будут являться квадратом единиц измерения элементов совокупности, например, исходные единицы совокупности измеряются в тоннах (т), тогда единица измерения дисперсии, вычисленной по этой совокупности будет т2 (тонна в квадрате). Естественно, в этом случае очень тяжело судить о степени разбросанности значений совокупности от средней величины. Именно поэтому и вводится новая величина, тесно связанная с дисперсией – среднее квадратическое отклонение (СКО) или стандартное отклонение. Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются индивидуальные значения признака от своего среднего значения. При изучении коэффициента вариации v следует обратить внимание на тот факт, что при изучении нескольких совокупностей имеющих различную природу, а, следовательно, и различные единицы измерения, невозможно сравнивать величину дисперсии, которая будет измеряться в разных величинах. Для таких сравнений необходимо использовать относительную величину. В качестве такой относительной величины и стали использовать коэффициент вариации. В ходе изучения правила сложения (или разложения) дисперсии необходимо пояснить, что изучаемое правило сложения дисперсии справедливо только для случая, когда совокупность сгруппирована по одному единственному признаку. Если же это не так, то для этого случая используются более сложные методы многомерного статистического анализа, который в рамках данного курса не рассматривается. Особо следует обратить внимание на возможность количественного определения тесноты связи между рассматриваемыми признаками на основе использования понятия межгупповой и общей дисперсий, путем вычисления эмпирического корреляционного отношения. Тема №7 «Выборочное наблюдение» В основе выборочного метода лежит предположение о том, что на основании вычисленных характеристик выборочной совокупности можно сделать о значениях характеристик генеральной совокупности. Это предположение получило научное обоснование в виде теоремы Чебышева. Особое внимание необходимо обратить на научно обоснованные способы формирования выборочной совокупности. В ходе отбора единиц выборочной совокупности необходимо обеспечить соблюдение следующих двух правил. а) выборка из генеральной совокупности должна быть проведена случайно, то есть каждая ее единица должна иметь такую же вероятность попасть в выборку, как и остальные (так, например, отобранные наилучшие или наихудшие единицы не отображают действительное распределение признака в генеральной совокупности); б) выборка должна быть осуществлена из однородной совокупности, так как при других обстоятельствах результаты выборки будут не точными и не могут в полной мере представлять генеральную совокупность. Нарушение этих принципов ведет к появлению систематической ошибки репрезентативности, что делает проведенное исследование ошибочным. В ходе обсуждения задач, возникающих при выборочном наблюдении необходимо обратить внимание на определение предельной ошибки выборки. Она определяется согласно теореме Ляпунова Δ = t∙μ где μ – средняя квадратическая ошибка выборки или стандартная ошибка выборки. Коэффициент доверия t при определении предельной ошибки зависит от принятого уровня вероятности Р: так, при t=1,0 значение вероятности Р=0,683; t=1,96 – для вероятности Р = 0,950; t=2,0 – для вероятности Р = 0,954; t=3,0 – для вероятности Р=0,997. Формулы для вычисления средней квадратической ошибки выборки или стандартной ошибки зависят от способа организации выборочного обследования. Для простой случайной бесповторной выборки и механической выборки для средней величины стандартная ошибка будет определяться по формуле 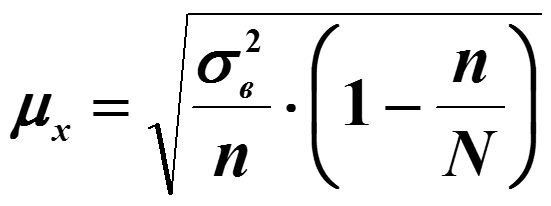 для доли 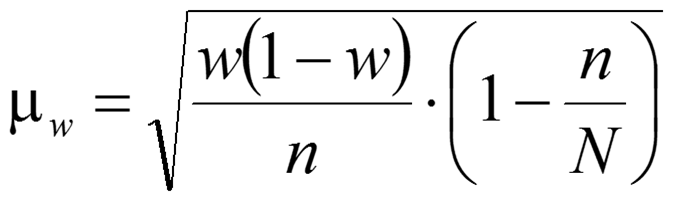 Для более сложных способов формирования выборочной совокупности стандартная ошибка такой выборки μ находится по формулам, известным из специальной литературы. При решении задачи о нахождении необходимой численности выборки, которая с практической достоверностью обеспечивала бы заданную точность выборочных характеристик используются следующие формулы а) для средней 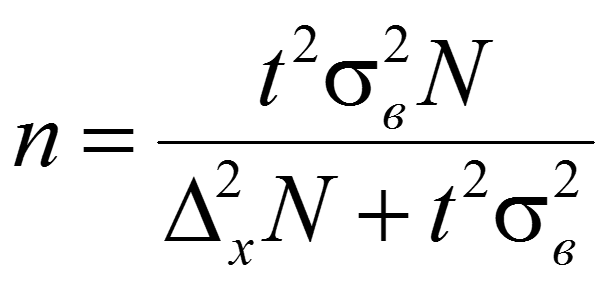 б) для доли 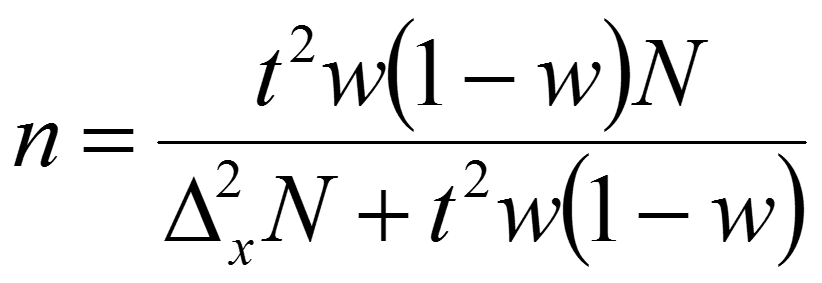 В данном случае в этих выражениях все величины известны или могут быть определены из таблиц, но выборочная дисперсия и для средней величины, и для доли, как правило, остается неизвестной. Возникает вопрос о том, как ее определить. Это возможно сделать одним из следующих способов – принять равной значениям из предыдущих выборочных наблюдений; – по правилу, согласно которому в размахе вариации R=xmax – xminукладывается примерно шесть стандартных отклонений. То есть в этом случае будет справедливо следующее соотношение R/σ = 6 или R2/σ2= 36. Тогда выборочная дисперсия будет определяться из соотношения σ2= R2/36. – по правилу «трех сигм», согласно которому в средней величине укладывается примерно три стандартных отклонения. В этом случае, используя выражение для коэффициента вариации, получим 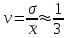 или или 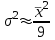 . .Тема №8. «Статистические методы анализа корреляционных связей» В ходе изучения различных социально-экономических явлений приходится сталкиваться с различными типами зависимостей. Как правило, различают функциональную и стохастическую зависимости. Под функциональной понимается такая зависимость, когда одному значению независимого фактора обычно соответствует только одно значение зависимого фактора, то есть с изменением одного фактора изменяется другой. При стохастической связи одному значению независимого фактора соответствует целое множество значений зависимого фактора с определенной вероятностью. Следует подчеркнуть последовательность решаемых задач при анализе корреляционных связей: устанавливается наличие корреляции (связи) между величинами; устанавливается формула линии связи (линии регрессии); определяются параметры линии регрессии по методу наименьших квадратов; определяются значимость установленной зависимости и достовер-ность отдельных параметров. Необходимо особо выделить необходимость проведения исследования адекватности полученной модели. Такое исследование обязательно содержит три этапа: проверка значимости или существенности коэффициента корреляции: выполняется с помощью t-критерия Стьюдента; проверка значимости или существенности коэффициентов, полученного уравнения регрессии: так же выполняется с помощью t-критерия Стьюдента; проверка значимости или предсказательной силы полученного уравнения регрессии: выполняется с помощью критерия Фишера. Значимость или существенность анализируемых параметров означает их отличность от нуля. Материалы данной темы используются в теме «Ряды динамики», как один из методов сглаживания рядов динамики: метод аналитического выравнивания и метод описания сезонных колебаний в рядах динамики. Тема №9 «Ряды динамики» Для оценки свойств динамики в статистике применяются взаимоувязанные характеристики, получившие название аналитических показателей. Среди них наиболее часто используются: абсолютный прирост, темп роста, темп прироста и абсолютное значение одного процента прироста. Но следует отметить, что кроме этого существует огромное количество показателей, которые также характеризуют различные стороны изучаемого явления, но которые в курс статистики не рассматриваются. Особо следует обратить внимание на способы расчета аналитических показателей: как и все статистические показатели они рассчитываются двумя способами: цепным и базисным. Из материала лекций следует определить эти способы расчета и взаимосвязь между показателями, рассчитанными по различным способам. Особо следует обратить внимание на то, что расчет такого показателя, как абсолютное значение одного процента прироста имеет экономический смысл только на цепной основе, поскольку на базисной основе для всех уровней будет получено то же значение показателя — сотая часть базисного (первого) уровня. Это следует из формулы вычисления данного показателя: если в данную формулу подставить исходные данные для базисного способа расчета, то сразу видно, что показатель будет соответствовать 0,01 показателя, приятого за базу сравнения, а так как при базисном способе расчета база сравнения не изменяется, то и значение показателя для всех уровней ряда будет одним и тем же. Каждый ряд динамики можно рассматривать как некую совокупность n меняющихся во времени показателей, которые можно обобщать в виде средних величин. Такие обобщенные (средние) показатели особенно необходимы при сравнении изменений того или иного показателя в разные периоды, в разных странах и т.д. Обобщенной характеристикой ряда динамики может служить прежде всего средний уровень ряда. Способ расчета среднего уровня зависит от того, моментный ряд или интервальный (периодный). В случае интервального ряда его средний уровень определяется по формуле простой средней арифметической величины из уровней ряда, т.е. 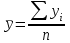 Если имеется моментный ряд, содержащий n уровней (y1, y2, …, yn) с равными промежутками между датами (моментами времени), то такой ряд легко преобразовать в ряд средних величин. При этом показатель (уровень) на начало каждого периода одновременно является показателем на конец предыдущего периода. Тогда средняя величина показателя для каждого периода (промежутка между датами) может быть рассчитана как полусумма значений у на начало и конец периода, т.е. как 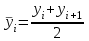 . Количество таких средних будет (n – 1). . Количество таких средних будет (n – 1).Эта средняя известна в статистике как средняя хронологическая для моментных рядов. Такое название она получила от слова «cronos» (время, лат.), так как рассчитывается из меняющихся во времени показателей. В случае неравных промежутков между датами среднюю хронологическую для моментного ряда можно рассчитать как среднюю арифметическую из средних значений уровней на каждую пару моментов, взвешенных по величине расстояний (отрезков времени) между датами, т.е. 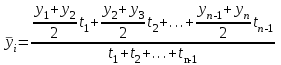 В данном случае предполагается, что в промежутках между датами уровни принимали разные значения, и мы из двух известных (yi и yi+1) определяем средние, из которых затем уже рассчитываем общую среднюю для всего анализируемого периода. Окончательно получаем формулу средней арифметической взвешенной: 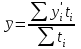 где 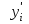 – средние уровни отдельных интервалов времени; ti – длительность соответствующих интервалов – средние уровни отдельных интервалов времени; ti – длительность соответствующих интервалов Рассматривая способы и методы выравнивания динамических рядов необходимо отметить, что в курсе «Статистики» изучаются следующие: а) увеличение интервалов; б) вычисление средних уровней для увеличенных интервалах; в) определение скользящей (подвижной) средней; г) аналитическое выравнивание. Тема №10 «Экономические индексы» При построении индексов используются количественный, качественные и смешанные показатели. В данной теме под количественными показателями понимаются показатели, характеризующие количественную сторону явления, например, объем произведенной продукции в натуральном выражении. Под качественными показателями понимаются показатели, характеризующие изучаемое явление с качественной стороны, например, цена продукции. Но и количественные и качественные показатели в данном случае имеют числовое выражение, просто они характеризуют изучаемое явление с разных сторон. При построении общего индекса физического объема продукции агрегатным способом следует иметь ввиду, в качестве соизмерителя, опять-таки как правило, принимается цена за единицу продукции, отнесенная к базисному периоду, то есть данный индекс запишется так 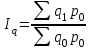 . .В качестве соизмерителя может выступать не только цена, но и другие качественные показатели. Единственное требование, чтобы произведение индексируемой величины на соизмеритель имело экономический смысл. В качестве такого соизмерителя может быть использована, например, себестоимость единицы продукции. В этом случае индекс будет записан в следующем виде 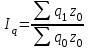 Если использовать в качестве соизмерителя другой качественный показатель – трудоемкость единицы продукции, то тогда индекс запишется так 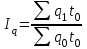 В этом случае такой индекс называют взвешенным по трудоемкости, тем самым подчеркивая, что в качестве соизмерителя использовалась трудоемкость единицы продукции. Следует обратить внимание на тот факт, что построение общих индексов может осуществляться двумя способами: агрегатным и с помощью средневзвешенных индексов. Наиболее часто используемым является агрегатный способ построения общих индексов. Но в том случае, когда для использования этого способа не хватает информации, используют метод средневзвешенных индексов, когда недостающую информацию пытаются заменить известными значениями индивидуальных индексов. |
