Тема 7 для студентов. Тема 7 Определение расстояний. Размер и форма Земли. Параллакс. Значение астрономической единицы. Определение размеров светил
 Скачать 66.4 Kb.
|
|
Тема 7: Определение расстояний. Размер и форма Земли. Параллакс. Значение астрономической единицы. Определение размеров светил. В астрономии нет единого универсального способа определения расстояний. По мере перехода от близких небесных тел к более далеким одни методы определения расстояний сменяют другие, служащие, как правило, основой для последующих. Точность оценки расстояний ограничивается либо точностью самого грубого из методов, либо точностью измерения астрономической единицы длины (а. е.). 1-й способ: По третьему закону Кеплера можно определить расстояние до тел СС, зная периоды обращений и одно из расстояний. 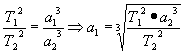 Приближённый метод.2-й способ: угломерный геометрический способ. Им определяют расстояния и до далеких звезд, к которым метод радиолокации неприменим. Геометрический способ основан на явлении параллактического смещения. П 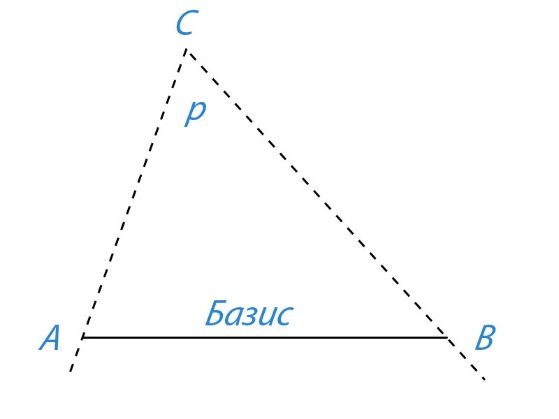 араллактическим смещением называется изменение направления на предмет при перемещении наблюдателя. Параллактические смещения светила тем больше, чем ближе оно к наблюдателю и чем больше перемещение наблюдателя.Параллакс — угол p, под которым из недоступного места (точка C) будет виден отрезок AB, называемый базисом. Базис — тщательно измеренное расстояние от точки A (наблюдатель) до какой-либо достигнутой для наблюдения точки B. Угол, под которым со светила виден экваториальный радиус Земли, перпендикулярный лучу зрения, называютсуточным параллаксом.Средний суточный параллакс Солнца равен 8,794", Луны — 57,04'. С годичным параллаксом связана и основная единица измерения расстояний между звездами —парсек(от параллакс и секунда): 1 пк = = 206 265 а. е. = 3,263 св. года = 3,086 · 1016м. Радиа́н — угол, соответствующий дуге, длина которой равна её радиусу. Радианная мера — угловая мера, в которой за единицу принимается угол в 1 радиан. То есть, радианная мера любого угла — это отношение этого угла к радиану. Из определения следует, что величина полного угла равна 2πрадиан. Определить радианную меру можно и так: радианная мера угла — отношение длины дуги окружности, находящейся между сторонами угла, к радиусу этой окружности, когда центр окружности совпадает с вершиной угла. Поскольку длина дуги окружности пропорциональна её угловой мере и радиусу, длина дуги окружности радиуса R и угловой величины α, измеренной в радианах, равна α ∙ R.   Пусть К - местонахождение наблюдателя, из которого светило видно на горизонте. Из рисунка видно, что из прямоугольного треугольника гипотенуза, расстояние D равно: , так как при малом значении угла если выражать величину угла в радианах и учитывать, что угол выражен в секундах дуги, а 1рад =57,30=3438'=206265", то и получается вторая формула. Угол (ρ) под которым со светила, находящегося на горизонте (? R - перпендикулярно лучу зрения) был бы виден экваториальный радиус Земли называется горизонтальным экваториальным параллаксом светила. Т.к. со светила никто наблюдать не будет в силу объективных причин, то горизонтальный параллакс определяют так: измеряем высоту светила в момент верхней кульминации из двух точек земной поверхности, находящихся на одном географическом меридиане и имеющем известные географические широты из полученного четырехугольника вычисляют все углы (в т. ч. параллакс).  D = 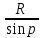 Зная расстояние до светила, можно определить его линейные размеры, если измерить его угловой радиус р. Формула, связывающая эти величины, аналогична формуле для определения параллакса: 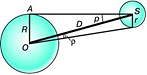 Учитывая, что угловые диаметры даже Солнца и Луны составляют примерно 30', а все планеты видны невооруженному глазу как точки, можно воспользоваться соотношением: sin р ≈ р. Если расстояние D известно, то r = D ρ, где величина ρ выражена в радианах. Задача: Зная горизонтальный параллакс Луны и экваториальный радиус Земли (6378 км), найти расстояние от Земли до Луны. 3 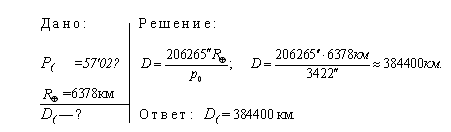 . Способ. Радиолокационный метод. Он заключается в том, что на небесное тело посылают мощный кратковременный импульс, а затем принимают отраженный сигнал. Скорость распространения радиоволн равна скорости света в вакууме: с = 299792458 м/с. Поэтому если точно измерить время, которое потребовалось сигналу, чтобы дойти до небесного тела и возвратиться обратно, то легко вычислить искомое расстояние. Идея непосредственного метода определения расстояния до небесных тел (в частности, расстояния между Землей и Луной) была обоснована отечественными физиками Л. И. Мандельштамом и Н. Д. Папалекси. Радиолокационные наблюдения позволяют с большой точностью определять расстояния до небесных тел Солнечной системы. Этим методом уточнены расстояния до Луны, Венеры, Меркурия, Марса, Юпитера. Для космических полетов необходимо с большой точностью определять значение астрономической единицы. Еще сравнительно недавно астрономическая единица была известна с точностью до нескольких десятков тысяч километров. Из радиолокационных наблюдений Венеры получено следующее значение астрономической единицы: 1 а. е. = (149 597 868 ± 0,7) км. Округленному значению астрономической единицы (149600000км) соответствует параллакс Солнца  = 8,7940′. |