Задание2. Тема. Анализ надежности не восстанавливаемых систем надежность не резервированной системы надежность простейших резервированных систем надежность систем при общем и раздельном резервировании
 Скачать 146.94 Kb. Скачать 146.94 Kb.
|
|
Тема. Анализ надежности не восстанавливаемых систем: надежность не резервированной системы; надежность простейших резервированных систем; надежность систем при общем и раздельном резервировании. Показатели безотказности. Основной изучаемой СВ для невосстанавливаемых изделий является наработка до первого отказа Т0. Если наработка измеряется в единицах времени, то она совпадает с календарным временем для изделий, работающих в режиме ОКРП (однократного применения) и НПДП (непрерывного длительного применения), и с суммарной длительностью выполненных циклов – для работающих в режиме МКЦП (многократного циклического применения). Если отказ может обесценивать часть наработки, то в наработку до отказа включают только ту ее часть, которая не обесценена отказом. Вероятностные характеристики наработки Т0 и являются показателями безотказности НВО (невосстанавливаемые объекты). Их особенность состоит в том, что они определяются по результатам наблюдений за некоторым множеством экземпляров однотипных изделий, но используются в качестве показателя надежности каждого конкретного изделия. Поэтому в дальнейшем кроме вероятностного приводятся и статистическое определение, которое можно использовать как один из способов статистической оценки искомой вероятностной характеристики. Вероятность безотказной работы Р(t) – это вероятность того, что изделие будет работоспособно в течение заданной наработки при заданных условиях эксплуатации: Р(t) = Р(Т0 > t). По статистическим данным об отказах вероятность безотказной работы определяют по формуле: где N0 – число изделий в начале наблюдения; n(t) – число отказавших за время t изделий. В начальный момент времени Р(0) = 1, если при включении отказы невозможны, и 0 < Р(0) < 1, если при включении изделие может отказать. При 27 увеличении времени вероятность Р(t) монотонно уменьшается и для любых технических изделий асимптотически приближается к нулю.Вероятность отказа Q(t) – это вероятность того, что при заданных условиях эксплуатации в течение заданной наработки произойдет хотя бы один отказ, то есть Q (t) = Р(Т0 < t). Отказ и безотказная работа – это противоположные события. Поэтому Q (t) = 1 – Р(t). Из (2) и (4) следует, что  Согласно (3) функцию Q(t) можно трактовать как функцию распределения СВ Т0. Дифференциал функции Q(t) называется элементом вероятности и представляет собой вероятность того, что отказ произойдет в бесконечно малой окрестности точки t: dQ (t) = Р(t ≤ Т0 < t + dt). Частота отказа α(t) – это плотность распределения времени безотказной работы (наработки) изделия до первого отказа. Согласно вероятностному определению: 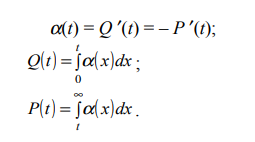 При наблюдении за работой N0 изделий можно определить частоту отказов как отношение числа отказавших в единицу времени изделий к общему числу изделий при условии, что отказавшие изделия не восстанавливаются: 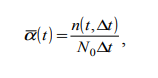 где n(t,∆t) = n(t +∆t / 2) – n(t −∆t / 2) – число отказавших изделий в интервале (t − ∆t / 2;t + ∆t / 2) . Интенсивность отказов λ(t) – это плотность распределения наработки до первого отказа при условии, что отказавшее изделие до рассматриваемого момента времени работало безотказно. Согласно вероятностному определению, 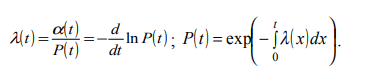 По статистическому определению, интенсивность отказов есть отношение числа отказавших в единицу времени изделий к среднему числу работоспособных на рассматриваемом отрезке времени изделий:  где Nср = N0 – ( n(t +∆t / 2) + n(t −∆t / 2) )/2. Поскольку существует однозначная связь между функциями Р(t), Q (t), α(t) и λ(t), достаточно задать лишь одну из них, чтобы по формулам связи найти все остальные, то есть в смысле полноты сведений о надежности изделия эти функции эквивалентны. Они определяются по статистическим данным о количестве отказов невосстанавливаемых изделий. Если же до начала интересующего нас интервала времени изделие уже проработало в течение времени τ, то для оценки надежности необходимо вводить условные показатели при условии, что изделие уже некоторое время проработало безотказно. Рассмотрим некоторые из этих параметров, считая, что одна из функций Р(t), Q (t), α(t) или λ(t) – известна. Вероятность безотказной работы Р(τ, t) в интервале (τ,τ + t) – это вероятность того, что отказа не будет в интервале τ + t, при условии, что его не было в течение времени τ :  где Р(t) – функция (1). Прочие показатели надежности определяются по формулам 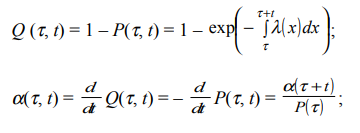  Средняя наработка до первого отказа T0 есть математическое ожидание наработки до первого отказа Т0. Используя определение элемента вероятности (6), можно записать: 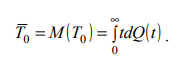 Если функция Q (t) дифференцируема при всех t > 0, то из (11) и (7) получим: 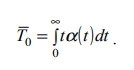 Заменяя в (11) d Q (t) на d P (t), интегрируя по частям и учитывая свойства функции P (t), имеем 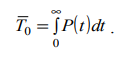 Отсюда следует, что средняя наработка до первого отказа равна площади под кривой P (t) на всей полуоси (0, ∞). По результатам наблюдения за работой до отказа всех N0 изделий можно составить следующую статистическую оценку средней наработки до первого отказа: 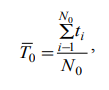 где ti – наработка до отказа i – го изделия. Средняя остаточная наработка до отказа (τ) T0 есть математическое ожидание СВ Т0 – τ при условии, что Т0 > τ . Используя функции (9) и (10), составим выражение для средней остаточной наработки до первого отказа: 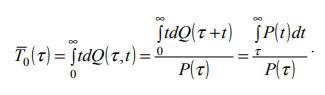 При τ = 0 функции (9), (10) и (13) совпадают с (1), (4), (7), (8) и (11). Показатели долговечности. При определении показателей долговечности вводятся следующие СВ: ресурс Тр – суммарная наработка изделия от начала эксплуатации до перехода в предельное состояние, установленное в технической документации; срок службы Тс – календарная продолжительность службы изделия от начала его эксплуатации до перехода в предельное состояние. Различают средний, гамма-процентный и назначенный ресурсы (срок службы). Средний и гамма-процентный ресурсы (срок службы) – это, соответственно, математическое ожидание СВ Тр (Тс) и квантиль по уровню вероятности γ, выраженному в процентах. Назначенный ресурс (срок службы) – это суммарная наработка (календарная продолжительность), по достижении которой эксплуатация изделия прекращается независимо от его технического состояния. Остаточный ресурс Тро (срок службы Тсо) – это суммарная наработка (календарная продолжительность) от момента контроля технического состояния до перехода в предельное состояние. Аналогично вводятся понятие остаточного срока хранения Тхро. Для СВ Тро, Тсо, Тхро используются те же характеристики, что и для Тр, Тс, Тхр. Показатели сохраняемости. Для оценки сохраняемости рассматривают характеристики СВ – срока сохраняемости, определяемой как календарная продолжительность хранения и/или транспортирования изделия, в течение которой сохраняются в заданных пределах значения параметров, характеризующих способность изделия выполнять заданные функции. В качестве показателей сохраняемости используют средний и гамма-процентный сроки сохраняемости. Практическое занятие №1 Расчет показателей надежности не резервированных не восстанавливаемых систем Задача 1.6. На испытание поставлено N = 400 изделий. За время t = 3000 час отказало 200 изделий, т.е. n(t) = 400 – 200 = 200. За интервал времени ∆t, где t = 100 час, отказало 100 изделий, т.е. n(t) = 100. Требуется определить Р(3000), P(3100), f (3000), λ(3000). Решение: По формуле (1.1) находим  Используя формулы (1.3) и (1.4), получим Задача 1.7. На испытание поставлено 100 однотипных изделий. За 4000 час отказало 50 изделий. За интервал времени 4000 - 4100 час отказало ещё 20 изделий. Требуется определить f(t), λ(t) при t = 4000 час. Решение: В данном случае N=100; t=4000 час; Δt =100 час; Δn(t)=20; n(t)=50. Задача 1.8. На испытание поставлено 100 однотипных изделий. За 4000 час отказало 50 изделий. Требуется определить P0(t) и Q0 (t) при t = 4000 час. Решение: В данном случае N= 100; n(t)=100-50=50; N-n(t)=100-50=50. По формулам определяем: Р(4000)=50/100=0,5 q(4000)=50/100=0,5 Задача 1.9. В течение 1000 час из 10 гироскопов отказало 2. За интервал времени 1000 - 1100 час отказал еще один гироскоп. Требуется определить f(t), λ(t) при t =1000 час. Решение: В данном случае N=10; t=1000 час; Δt =100 час; Δn(t)=1; n(t)=8. f*(1000)=1/10*100=1*10-2 1/час λ*(1000) = 1/ 100*8 = 1,25*10 1/час Задача 1.10. На испытание поставлено 1000 однотипных электронных ламп. За первые 3000 час отказало 80 ламп. За интервал времени 3000 - 4000 час отказало еще 50 ламп. Требуется определить P0(t) и Q0 (t) при t = 4000 час. Решение: В данном случае N= 1000; n(t)=1000-80-50=870; N-n(t)=1000-870=130. По формулам определяем: q*(t) = 1000-870/1000=1,3*10-2 1/час p*(t) = 870/1000=8,7*10-2 1/час Задача 1.11. На испытание поставлено 1000 изделий. За время t = 1300 час вышло из строя 288 штук изделий. За последующий интервал времени 1300-1400 час вышло из строя еще 13 изделий. Необходимо вычислить P0(t) при t = 1300 час и t =1400 час; f(t), λ(t) при t =1300 час. Решение: В данном случае N=1000; t=1300 час; Δt =100 час; Δn(t)=13; n(t)=288; n(1300)=1000-288=712;n(1400)=1000-288-13=699 Задача 1.12. На испытание поставлено 45 изделий. За время t = 60 час вышло из строя 35 штук изделий. За последующий интервал времени 60-65 час вышло из строя еще 3 изделия. Необходимо вычислить P0(t) при t = 60час и t = 65 час; P0(t) при t = 60 час. Решение: В данном случае N=45; t=60 час; Δt =5 час; Δn(t)=3; n(t)=35; n(60)=45-35=10; n(65)=45-35-3=7 Задача 1.13. В результате наблюдения за 45 образцами радиоэлектронного оборудования, которые прошли предварительную 80 - часовую приработку, получены данные до первого отказа всех 45 образцов, сведенные в табл.1.2. Необходимо определить mt. Таблица 1.2.  Решение: Задача 1.14. На испытание поставлено 8 однотипных изделий. Получены следующие значения ti (ti - время безотказной работы i-го изделия): t1 = 560 час; t2 = 700 час; t3 = 800 час; t4 = 650 час; t5 = 580 час; t6 = 760 час; t7 = 920 час; t8 = 850час. Определить статистическую оценку среднего времени безотказной работы изделия. Решение: Стат оценка ср вр-ни безотк работы 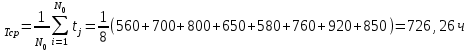 Задача1.15. За наблюдаемый период эксплуатации в аппаратуре было зарегистрировано 6 отказов. Время восстановления составило: t1 = 15 мин; t2 = 20 мин; t3 = 10 мин; t4 = 28 мин; t5 = 22 мин; t6 = 30 мин. Требуется определить среднее время восстановления аппаратуры mtâ . Решение: Среднее время восстан-ния аппаратуры Задача1.16. На испытание поставлено 1000 изделий. За время t = 11000 час вышло из строя 410 изделий. За последующий интервал времени 11000-12000 час вышло из строя еще 40 изделий. Необходимо вычислить P0(t) при t = 11000 час и t = 12000 час, а также f(t), λ(t) при t = 11000 час. Решение: P*(11000)=n(t)/N=590/1000=0,59 P*(12000)=n(t)/N=40/1000=0,04 f*(11000)=Δn(t)/N*Δt=40/1000*1000=0,04*10-3 1/час λ*(е)= Δn(t)/Δt*n(t)=40/1000*590=0,07*10-3 1/час |
