№ СЛАЙДА
|
ЧТО ДОЛЖНО БЫТЬ В СЛАЙДЕ
|
ЧТО НУЖНО ЗНАТЬ
|
1
|
Тема дипломной работы
Выполнил: студент группы Ф.И.О. студента
Научный руководитель:и.о.доцента к.т.н. Крахмалева Ю.Р.
|
|
|
2-4 слайд см. Введение ДР
|
|
2
|
Актуальность темы. При решении как теоретических, так и прикладных задач в самых различных разделах математики возникает класс специальных функций. Особое место в классе специальных функций занимают так называемые, функции- интегралы, изучение которых основано на функциях, зависящих от параметра. В связи с широким применением в различных приложениях данной теории и развитием компьютерных технологий возникает необходимость нахождения более рациональных путей практической реализации функций, зависящих от параметра. Одним из таких путей предлагается применение систем компьютерной математики.
|
|
3
|
Научная новизна. Методика вычисления функций, зависящих от параметра, посредством пакета компьютерной математики Maple открывает возможность использования в фундаментальных исследованиях.
Практическая значимость. Методика вычисления функций, зависящих от параметра, посредством пакета компьютерной математики Maple освобождает процесс вычисления от рутинных выкладок с минимальной затратой по времени.
|
|
4
|
Целью работы является исследование функций, зависящих от параметра и их практическая реализация посредством пакета компьютерной математики Maple.
Объект исследования. Функции, зависящие от параметра  : :
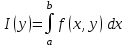
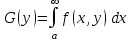
Предмет исследования: методы математического анализа
|
|
5
|
Название слайда: Определение функции от параметра
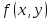 определена для всех значений определена для всех значений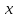 в некотором промежутке в некотором промежутке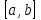 и всех значений и всех значений в множестве в множестве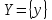 , , 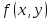 интегрируема на интегрируема на 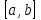 при каждом постоянном значении при каждом постоянном значении из из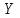 . Тогда собственный интеграл . Тогда собственный интеграл
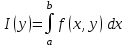
называется функцией от параметра  . .
Определение 1. Если для функции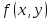 выполняются условия: выполняются условия:
1)при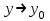 существует конечная предельная функция при существует конечная предельная функция при 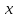 : : 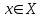
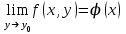
2) для любого числа 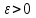 найдется такое не зависящее от найдется такое не зависящее от 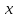 число число 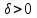 , что , что
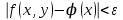
при 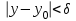 сразу для всех сразу для всех 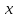 из из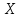 , то , то
функция 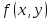 стремится к предельной функции стремится к предельной функции 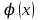 равномерно относительно равномерно относительно 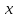 в области в области 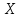 . .
|
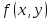 интегрируема на интегрируема на 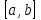 при каждом постоянном значении при каждом постоянном значении из из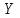 : :
интегрирование понимается в собственном или в несобственном смысле.
Определение 1 можно распространить на случай несобственного числа 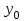 (например, (например,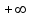 ). И в этом случае, неравенство ). И в этом случае, неравенство 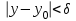 заменяется на неравенство заменяется на неравенство 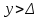 . .
|
6
|
Название слайда: Непрерывность функции от параметра
Теорема 1.Если функция 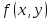 является интегрируемой по является интегрируемой по 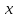 в в 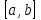 , при этом равномерно стремиться при , при этом равномерно стремиться при 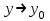 к к 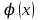 относительно относительно 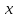 , тогда справедливо равенство: , тогда справедливо равенство:
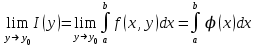 (1) (1)
Следствие. Если функция 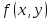 является непрерывной по является непрерывной по 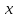 в в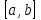 при постояном при постояном  ; при возрастании ; при возрастании  стремится к непрерывной же предельной функции, при этом монотонно возрастает, то имеет место (1). стремится к непрерывной же предельной функции, при этом монотонно возрастает, то имеет место (1).
Теорема 2 .Пусть функция 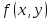 определена в прямугольнике определена в прямугольнике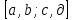 и является непрерывной, как функция от двух переменных, ,тогда можно утверждать, что и является непрерывной, как функция от двух переменных, ,тогда можно утверждать, что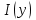 будет также непрерывной функцией от параметра будет также непрерывной функцией от параметра  в промежутке в промежутке 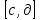 . .
|
Записать формулу можно в сокращенном виде:
.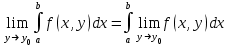 , ,
что означает:предельный переход по параметру допустим под знаком интеграла.
|
7
|
Название слайда: Дифференцируемость функции от параметра
Правило Лейбница вычисления производной функции 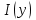 выполняется при допущении существования частной производной по аргументу выполняется при допущении существования частной производной по аргументу  : : 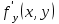 подынтегральной функции подынтегральной функции 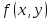 : :
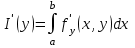 . (2) . (2)
Теорема 3 .Если функция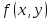
1)определена в прямоугольнике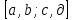 ; ;
2) непрерывна по аргументу 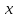 в в 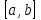 при всяком при всяком  в в 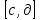 ; ;
3) существует 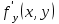 , которая непрерывна как функция , которая непрерывна как функция 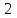 -х переменных, -х переменных,
Тогда справедлива формула (2)при любом значении  из из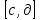 . .
|
Формула (2) записана в обозначениях Лагранжа. Существует запись правила Лейбница в обозначениях Коши:
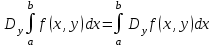
Если принимается перестановка знаков производной по аргументу  интеграла по аргументу интеграла по аргументу 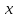 , то можно утверждать , что функция , то можно утверждать , что функция 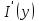 дифференцируема по параметру под знаком интеграла. Введенное правило Лейбницем для вычисления производной по параметру носит название «правилоЛейбница». дифференцируема по параметру под знаком интеграла. Введенное правило Лейбницем для вычисления производной по параметру носит название «правилоЛейбница».
Для применения правила Лейбница нужны условия, которые рассматриваются в теореме 3.
|
8
|
Название слайда: Интегрирование функции от параметра
Теорема 4.Если функция 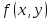 непрерывна (по обеим переменным) в прямоугольнике непрерывна (по обеим переменным) в прямоугольнике 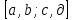 , то функция , то функция 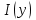 интегрируема на интегрируема на 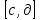 и имеет место формула (3) : и имеет место формула (3) :
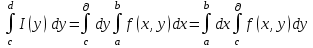
Пример 1. Проинтегрировать по параметру :
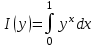 . .
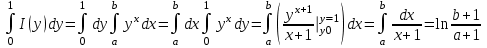
Пример 2. Проинтегрировать по параметру :
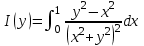
в прямоугольнике 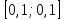 . .
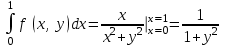 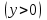 , ,
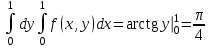 . .
в то время как:
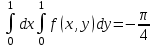
|
При наличии формулы (3), говорят что функцию 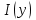 можно интегрировать по параметру можно интегрировать по параметру  под знаком интеграла(взятого по переменной под знаком интеграла(взятого по переменной 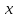 ). ).
Функция 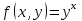 в прямоугольнике в прямоугольнике 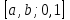 , где , где 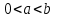 непрерывна. Условия теоремы 4 соблюдены. непрерывна. Условия теоремы 4 соблюдены.
Условия теоремы не выполнены: налицо разрыв в точке 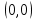 . .
|
8
|
Название слайда: Несобственные интегралы, зависящие от параметра
Пусть функция 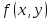 определена при всех определена при всех 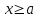 , при всех , при всех  и некоторого множества и некоторого множества 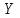 и при каждом фиксированном и при каждом фиксированном  : : 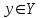 интегрируема на интегрируема на 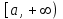 . Функция . Функция
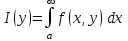
называется несобственным интегралом первого рода, зависящим от параметра.
Пусть функция 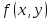 определена при всех определена при всех 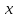 : : 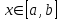 и при всех и при всех  : :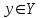 и при каждом фиксированном и при каждом фиксированном  является неограниченной при является неограниченной при 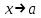 . Функция . Функция
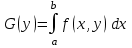
называется несобственным интегралом второго рода, зависящим от параметра.
Так как
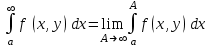
то
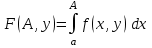 . .
|
При этом 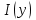 является сходящимся является сходящимся
Наряду с несобственным интегралом первого рода, вводится определение несобственного интеграла второго рода.
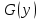 интеграл сходящийся интеграл сходящийся
Это определение несобственного интеграла:
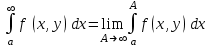
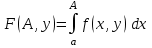 функцию от функцию от 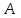 и и  , при , при 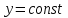 и и 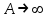 имеет пределом имеет пределом 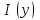 . Если стремление . Если стремление 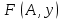 к к 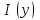 происходит равномерно относительно происходит равномерно относительно  в области в области 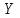 , то интеграл называют равномерно сходящимся относительно , то интеграл называют равномерно сходящимся относительно  для указанных значений параметра. для указанных значений параметра.
|
9
|
Название слайда: Интегрирование несобственного интеграла, зависящего от параметра
Теорема 5. Пусть функция 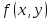 определена и непрерывна (как функция двух переменных) для значений определена и непрерывна (как функция двух переменных) для значений 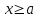 и значений и значений  в промежутке в промежутке 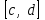 . Если функция . Если функция
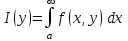
сходится равномерно относительно  : :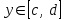 , то имеет место формула: , то имеет место формула:
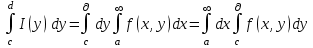
Пример 3. Найти значение интеграла
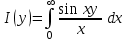 . .
Решение .Рассмотрим 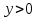 . Вводим замену переменных . Вводим замену переменных 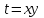 , тогда , тогда 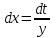 , тогда: , тогда:
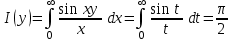 ; ;
При 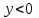 произведем замену переменной, полагая произведем замену переменной, полагая 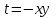 , , 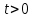 , имеем: , имеем:
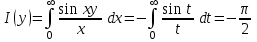
При 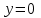 интеграл интеграл 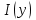 равен нулю. Следовательно, равен нулю. Следовательно,
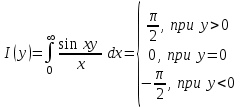 . .
|
|
10
|
Пример 4. Найти значение интеграла
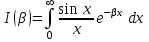 , ,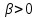 . .
Решение.
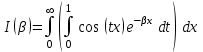 , ,
так как
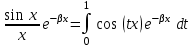 . .
Функция
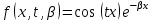
удовлетворяет условиям Теоремы 5, тогда
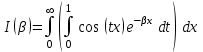 . .
Функция 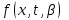 является непрерывной на промежутке является непрерывной на промежутке 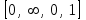 . где . где 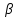 пусть принимает фиксированное значение , а пусть принимает фиксированное значение , а 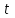 является параметром. Так как для является параметром. Так как для 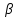 : : 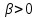 интеграл интеграл 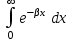 сходится и выполняется : сходится и выполняется :
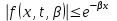
при 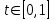 , то , то 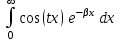 сходится равномерно на сходится равномерно на 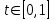 . Применяя интегрирование по частям, получим: . Применяя интегрирование по частям, получим:
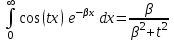 . .
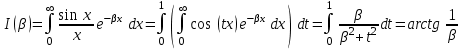
|
|
10
|
Название слайда: Интегрирование функций от параметра в Maple
restart;
Int((sin(x*y))/x,x=0..+infinity)=int((sin(x*y))/x,x=0..+infinity);
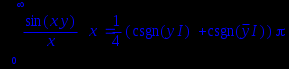
assume(y>0);
Int((sin(x*y))/x,x=0..+infinity)=int((sin(x*y))/x,x=0..+infinity);
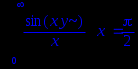
assume(y<0);
Int((sin(x*y))/x,x=0..+infinity)=int((sin(x*y))/x,x=0..+infinity);
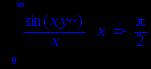
assume(y=0);
Int((sin(x*y))/x,x=0..+infinity)=int((sin(x*y))/x,x=0..+infinity);
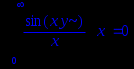
|
Рассмотрим решение в пакете компъютерной математики Maple. Значение функции, зависящей от параметра в таких случаях может зависить от знака параметра или каких-либо других ограничений. Вводим команду вычисления интеграла отложенного и прямого действия:
Для получения явного аналитического результата вычислений следует сделать какие- либо предположения о значении параметров, тем самым наложить на них ограничения. Для того используем assume(expr) , где expr – неравенство, которое содержит ограничение для параметра
|
11
|
Название слайда: Интегрирование функций от параметра в Maple
restart;
Int((exp(-betta*x)*(sin(x))/x),x=0..+infinity)=int((exp(-betta*x)*(sin(x))/x),x=0..+infinity);
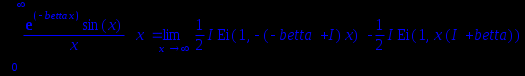 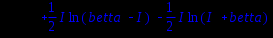
restart;
assume(betta>0);
Int((exp(-betta*x)*(sin(x))/x),x=0..+infinity)=int((exp(-betta*x)*(sin(x))/x),x=0..+infinity);
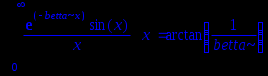
|
Значение интеграла в системе Maple показывает определение несобственного интеграла, но не его значение.
Решение примера выполнялось при 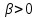 . Введем это ограничение и реализуем решение в системе Maple. . Введем это ограничение и реализуем решение в системе Maple.
Этот же результат получен и при решении примера, используя метод интегрирования по частям. Как видим, система находит выражение функции, зависящей от параметра без каких-либо трудностей.
|
12
|
Заключение(см. заключения ДР)
Разделом математики, в котором изучается функции, их задание и их поведение в определенной области является математический анализ. Один из способов задания функций основан на использовании интегралов, зависящих от параметров. Этот способ распространен в теории специальных функций.
В дипломной работе проводится исследование функций, зависящих от параметра и их практическая реализация посредством компьютерной математики Maple. В результате исследований показана ограниченность интегрирования функций, зависящих от параметра в системе. Разработана методика вычисления функций, зависящих от параметра посредством пакета компьютерной математики Maple, которая освобождает процесс вычисления от рутинных выкладок с минимальной затратой по времени.
|
|
13
|
Спасибо за внимание!
|
|
 Скачать 206.62 Kb.
Скачать 206.62 Kb.