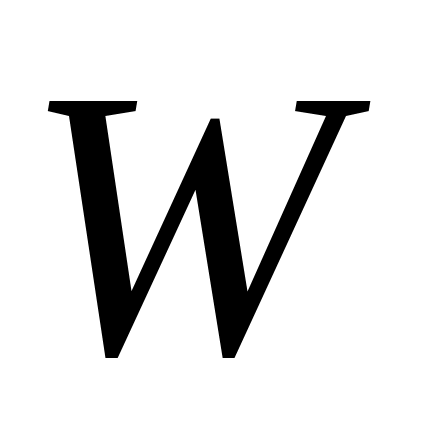 равен единице, если все ранжировки экспертов одинаковы, и равен нулю, если все ранжировки различны, т. е. совершенно нет совпадения. равен единице, если все ранжировки экспертов одинаковы, и равен нулю, если все ранжировки различны, т. е. совершенно нет совпадения.
Коэффициент конкордации, вычисляемый по формуле (2.10) или (2.11), является выборочной оценкой истинного (теоретического) значения коэффициента и, следовательно, представляет собой случайную величину. Для определения значимости оценки коэффициента конкордации необходимо знать распределение частот для различных значений числа экспертов 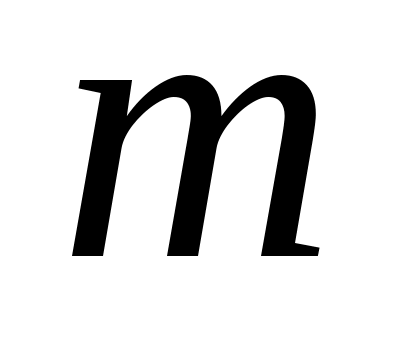 и количества альтернатив и количества альтернатив 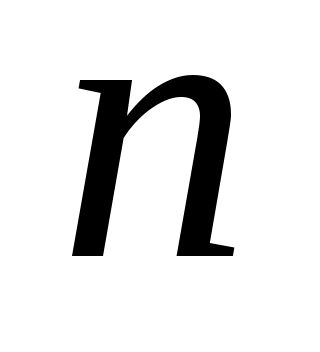 . .
Для малых значений 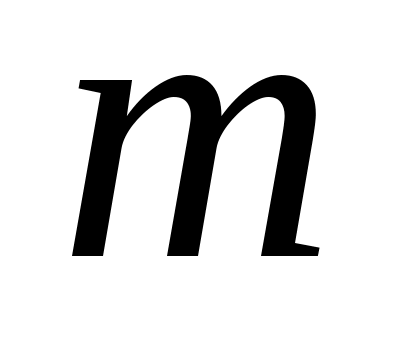 и и 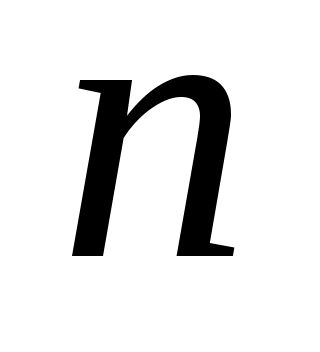 ( (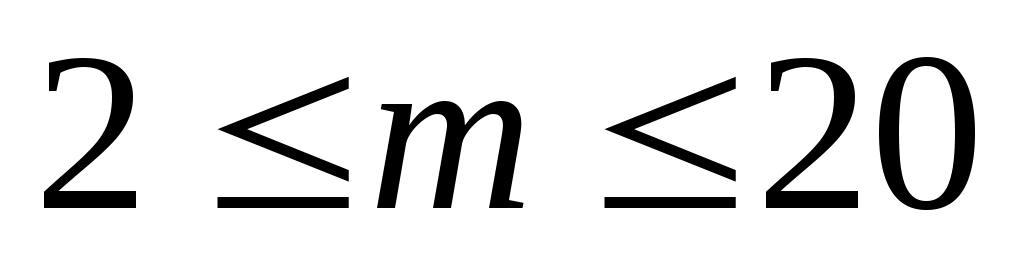 , , 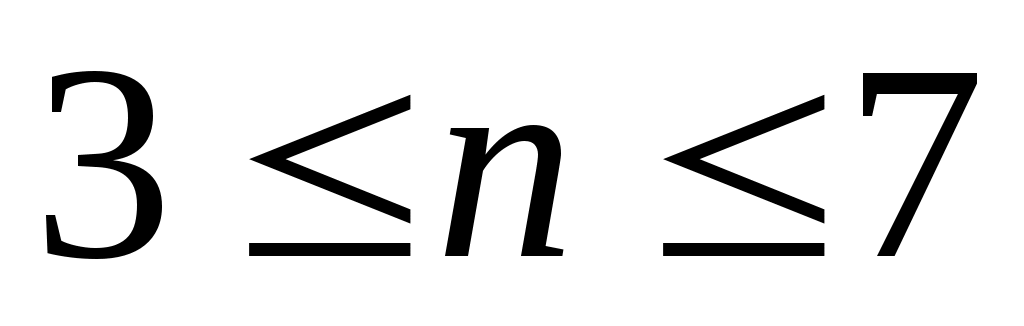 ) с помощью соответствующих таблиц 3П – 6П значений величины ) с помощью соответствующих таблиц 3П – 6П значений величины 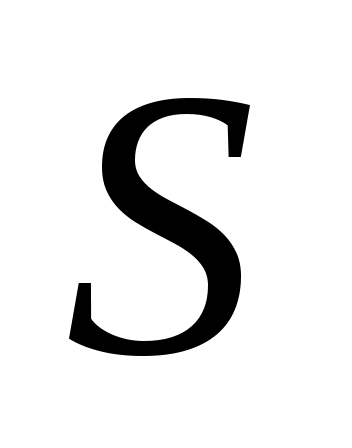 , приведенных в Приложении, где , приведенных в Приложении, где
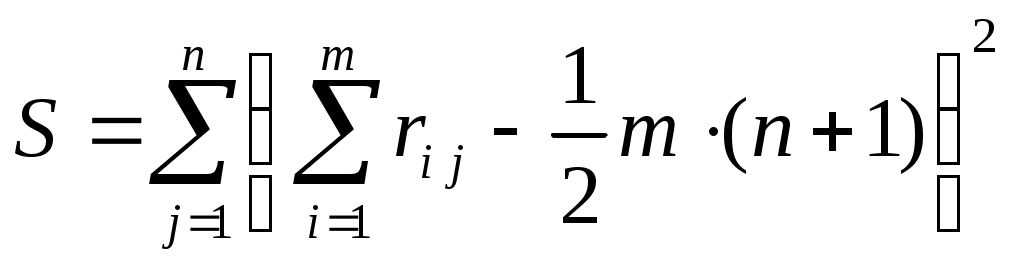 , ,
может быть получен ответ на вопрос о том, как сильно могут отклоняться от нуля выборочные значения коэффициента конкордации 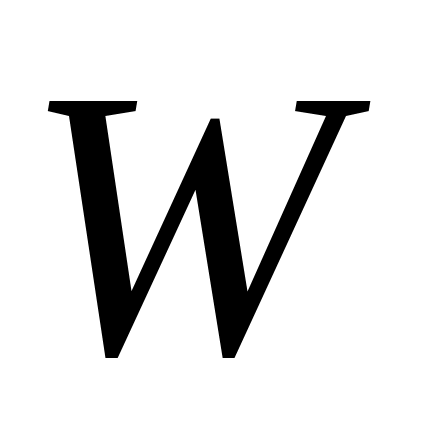 в ситуации, когда значение теоретического коэффициента конкордации в ситуации, когда значение теоретического коэффициента конкордации 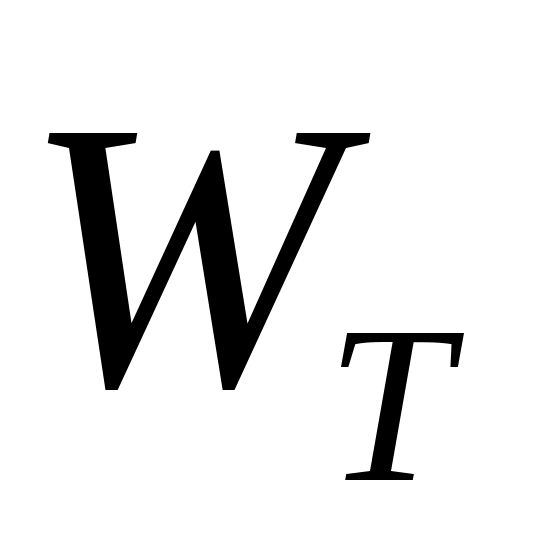 свидетельствует о полном отсутствии связи между анализируемыми ранжировками. свидетельствует о полном отсутствии связи между анализируемыми ранжировками.
«Входами» в эту таблицу является тройка чисел (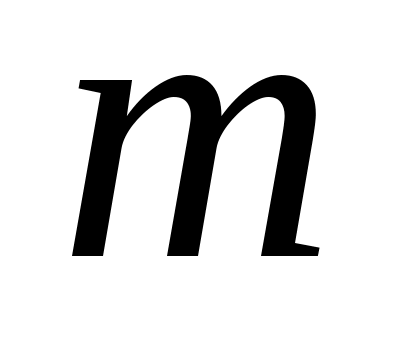 , , 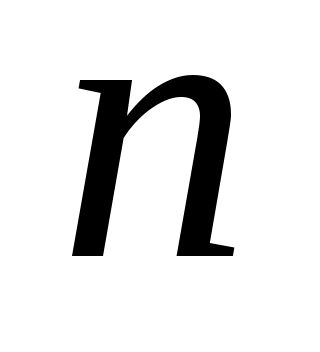 , , 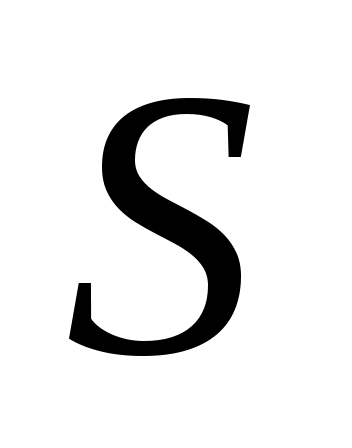 ), «выходом» ‑ вероятность ), «выходом» ‑ вероятность 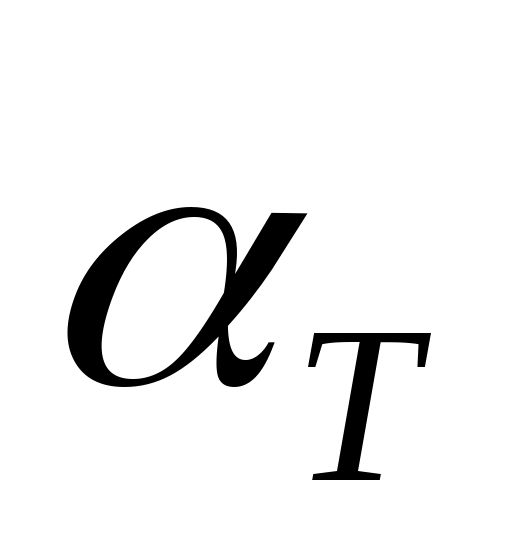 того, что величина того, что величина 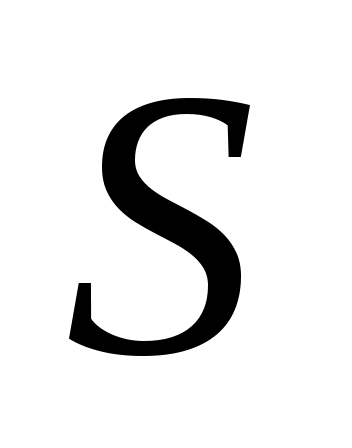 может быть такой, какой она является в нашей выборке, или большей в условиях отсутствия связи между ранжировками в генеральной совокупности. Если окажется, что эта вероятность меньше принятой нами величины уровня значимости критерия может быть такой, какой она является в нашей выборке, или большей в условиях отсутствия связи между ранжировками в генеральной совокупности. Если окажется, что эта вероятность меньше принятой нами величины уровня значимости критерия  (например, (например, 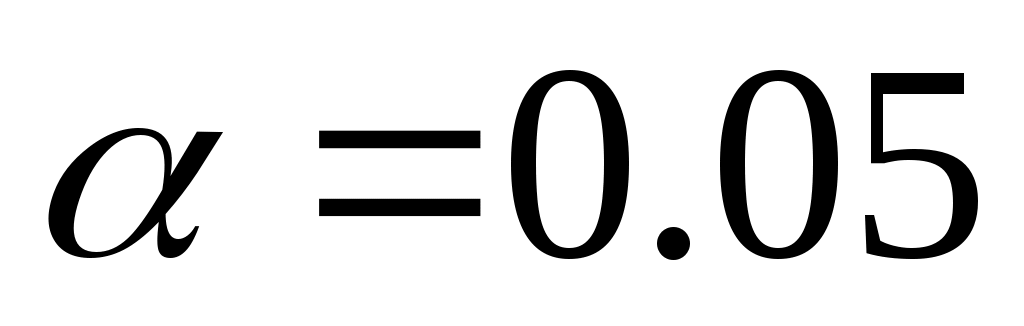 ), т.е. ), т.е. 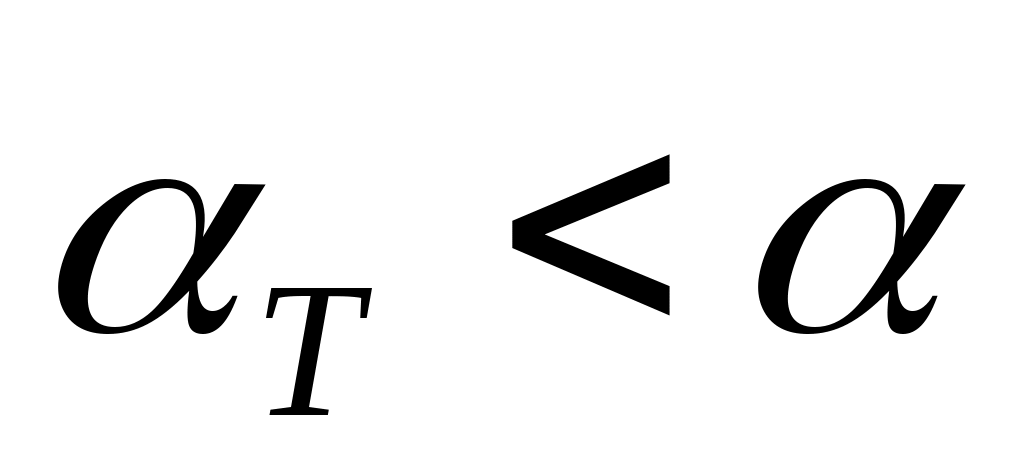 , то гипотезу об отсутствии связи следует отвергнуть, т.е. признать статистическую значимость анализируемой связи. , то гипотезу об отсутствии связи следует отвергнуть, т.е. признать статистическую значимость анализируемой связи.
Таблица 7П критических значений коэффициента конкордации 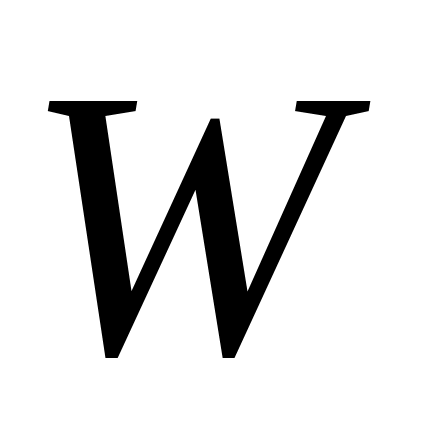 построена несколько иначе. В ней при уровне значимости построена несколько иначе. В ней при уровне значимости 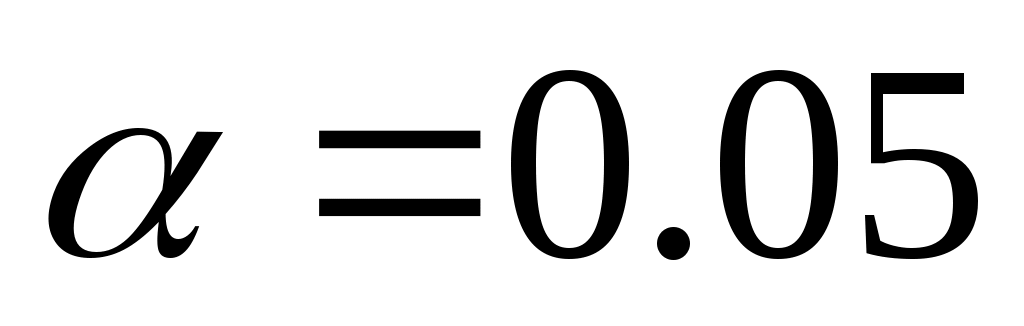 и в соответствии со «входами» ( и в соответствии со «входами» (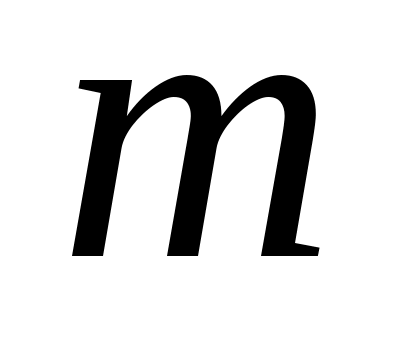 , ,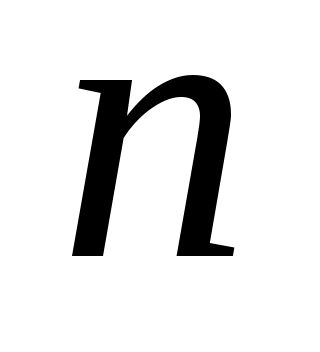 ) даны «критические» значения ) даны «критические» значения 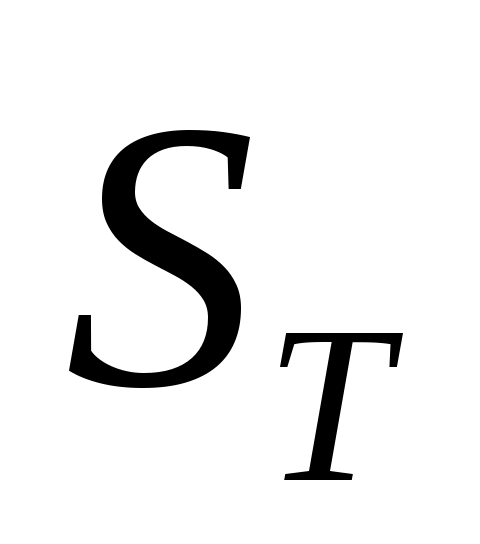 величины величины 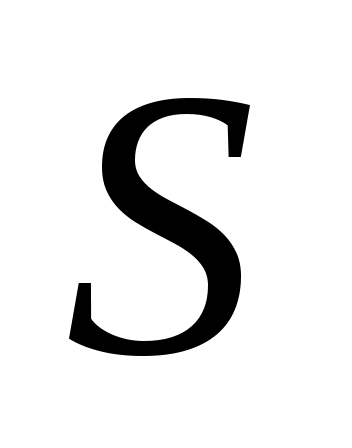 , т.е. такие значения, при превышении которых следует отвергать гипотезу об отсутствии связей между ранжировками (признавать их статистическую значимость). , т.е. такие значения, при превышении которых следует отвергать гипотезу об отсутствии связей между ранжировками (признавать их статистическую значимость).
См. пример 2.5, 2.6.
Для больших значений 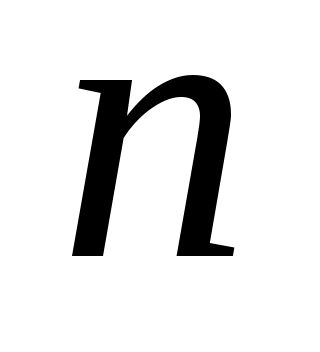 и и 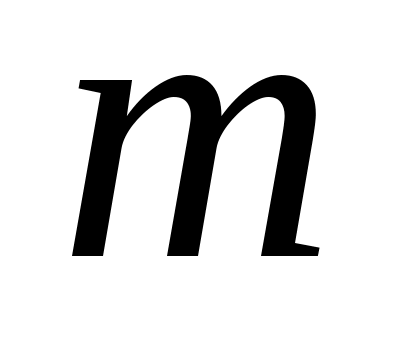 можно использовать известные статистики. При числе альтернатив можно использовать известные статистики. При числе альтернатив 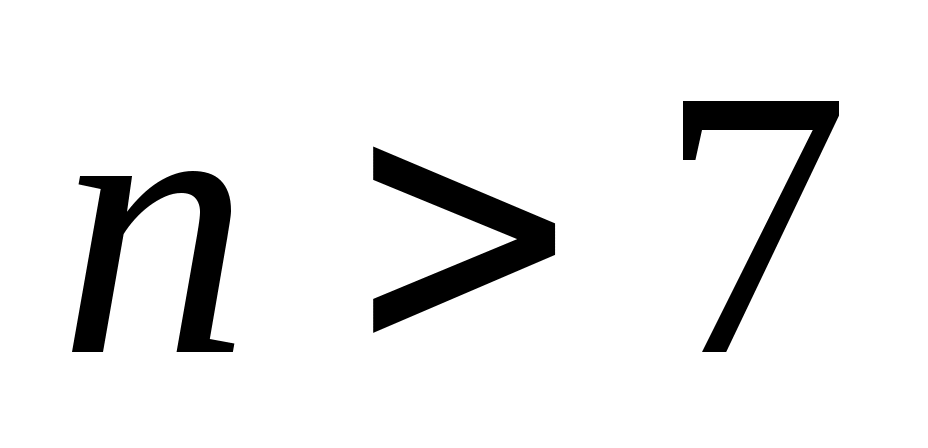 оценка значимости коэффициента конкордации может быть произведена по критерию оценка значимости коэффициента конкордации может быть произведена по критерию 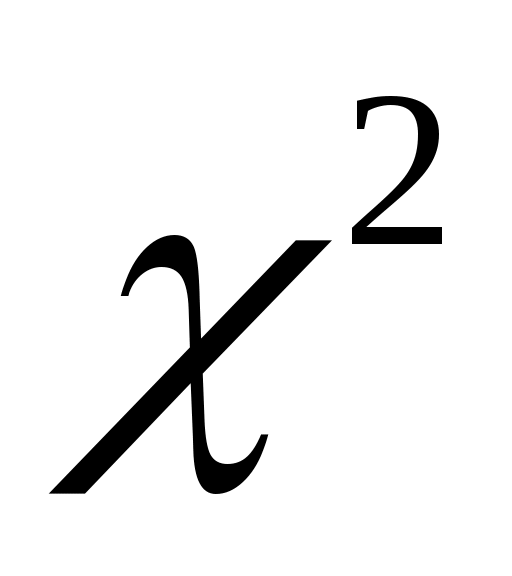 . Величина . Величина 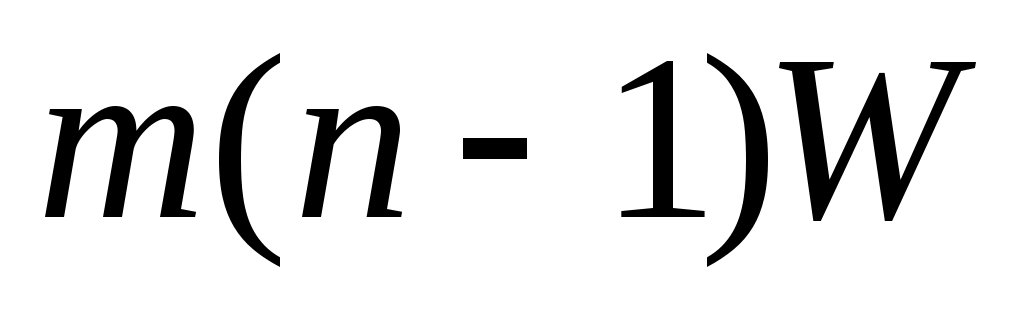 имеет имеет 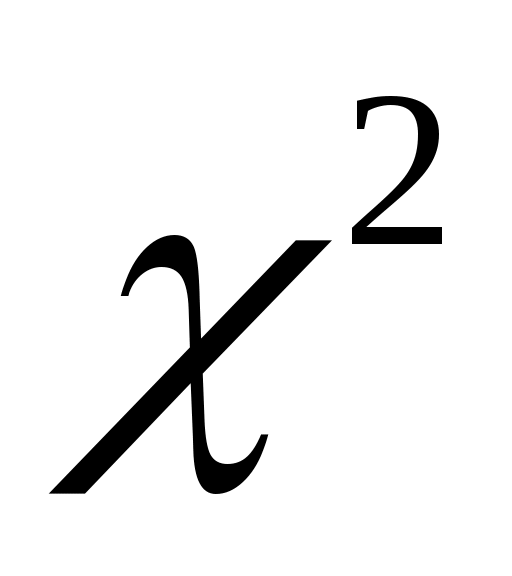 распределение с распределение с 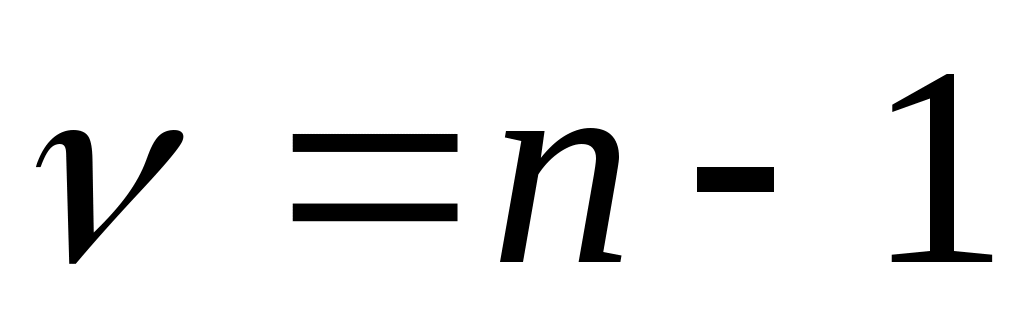 степенями свободы. Для оценки значимости степенями свободы. Для оценки значимости 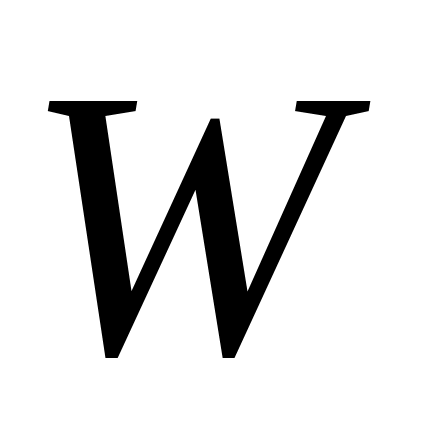 выбирают уровень значимости критерия выбирают уровень значимости критерия  (часто равный (часто равный 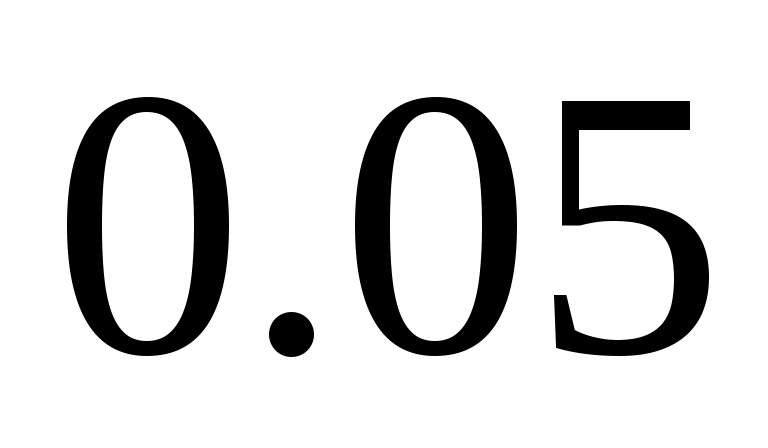 ), определяют по таблице 8П при ), определяют по таблице 8П при 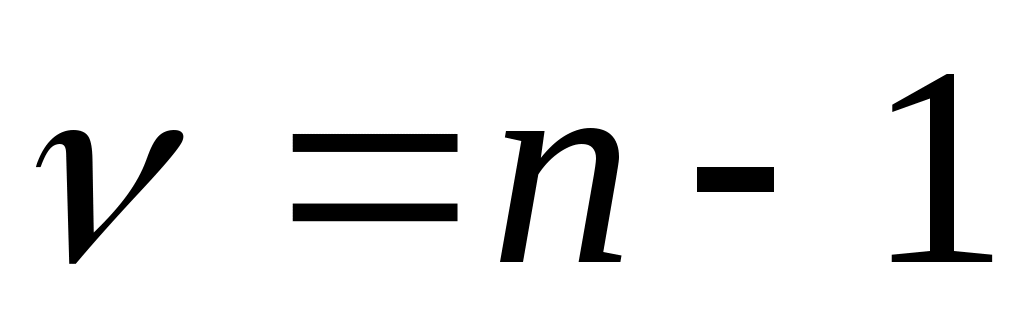 величину величину 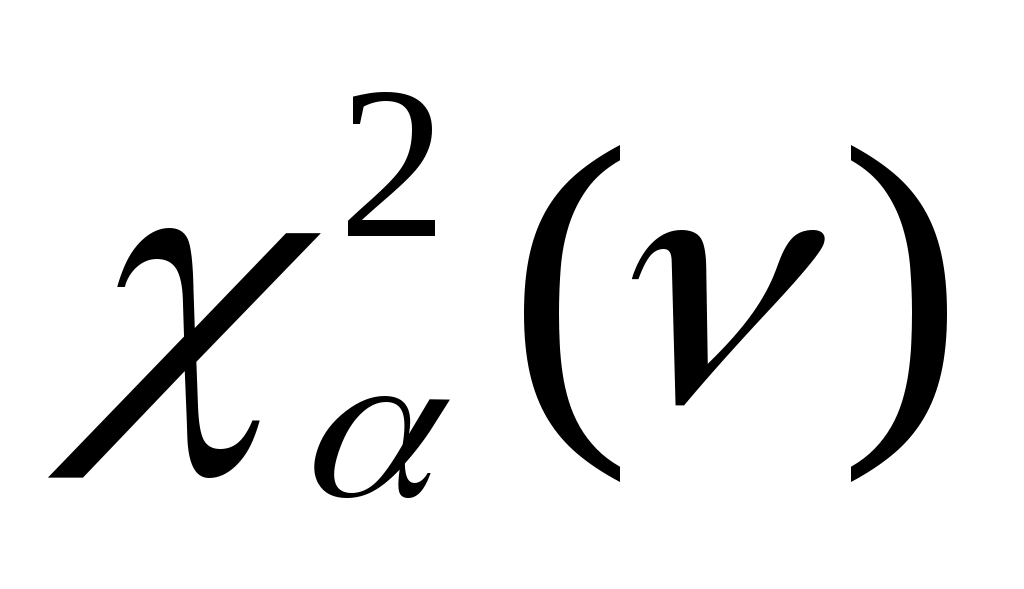 и если и если 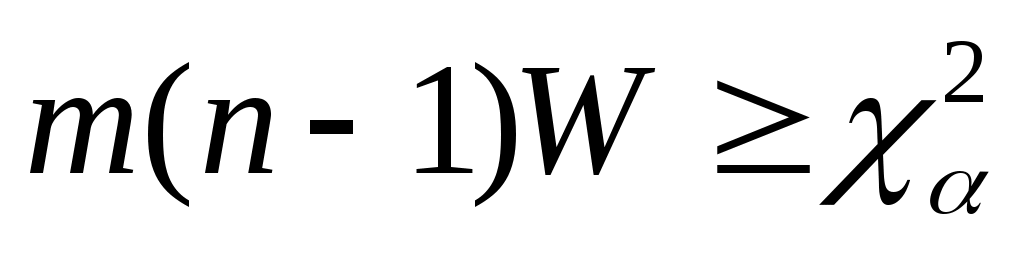 , то гипотезу об отсутствии связи между ранжировками следует отвергнуть (т.е. , то гипотезу об отсутствии связи между ранжировками следует отвергнуть (т.е. 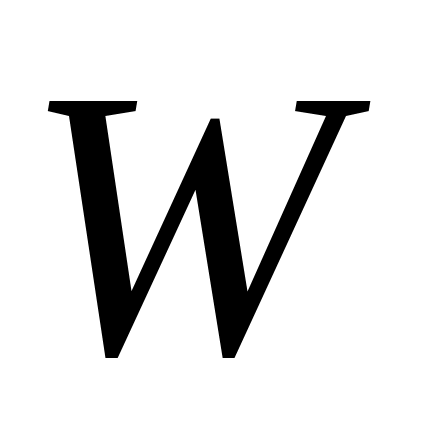 статистически значимое) и считать, что ранжировки связаны. статистически значимое) и считать, что ранжировки связаны.
Следующий пример иллюстрирует то, как оценивается значимость коэффициента конкордации Кендалла по критерию 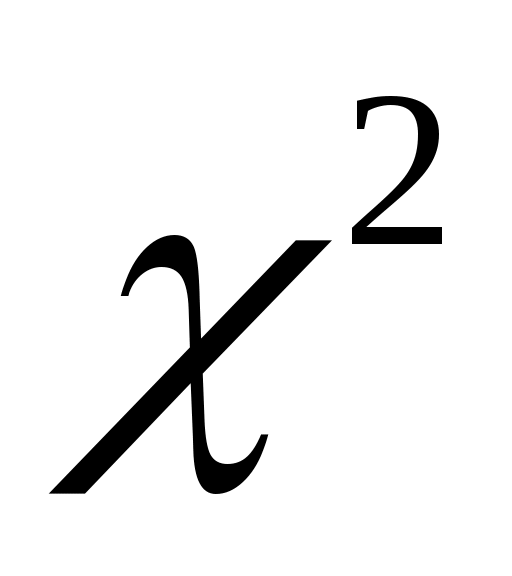 . .
См. пример 2.7.
Энтропийный коэффициент конкордации определяется формулой:
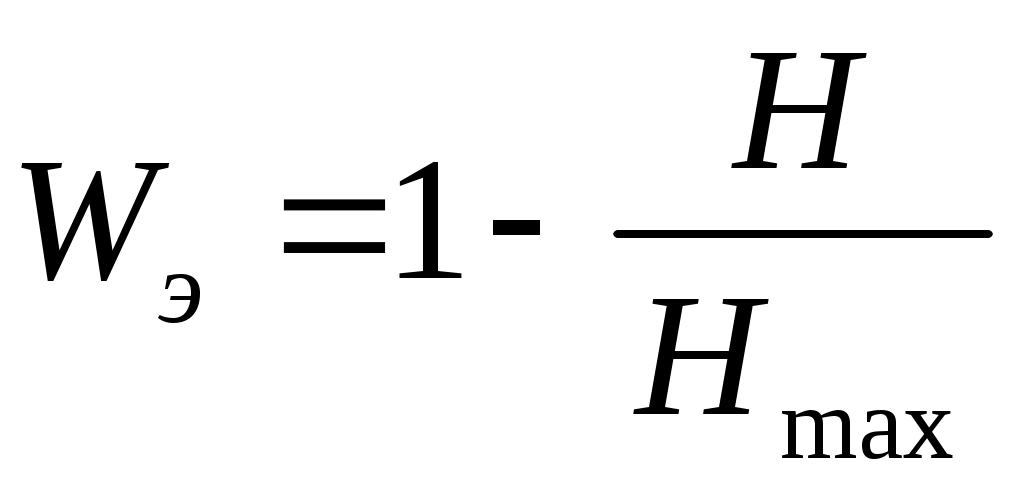 , ,
где  – энтропия, вычисляемая по формуле: – энтропия, вычисляемая по формуле:
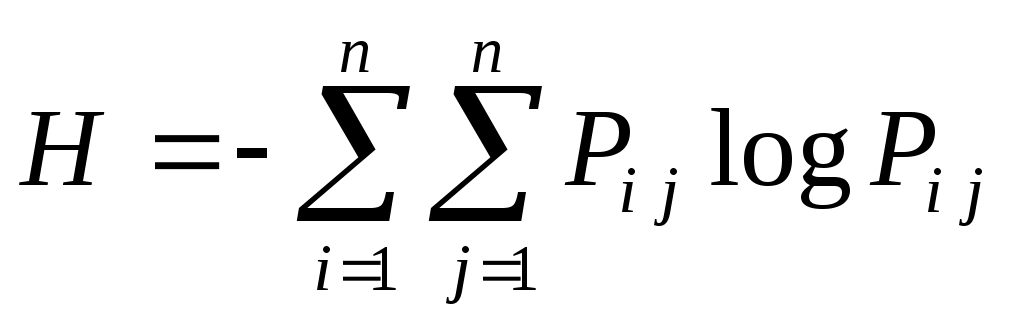 , (2.12) , (2.12)
где 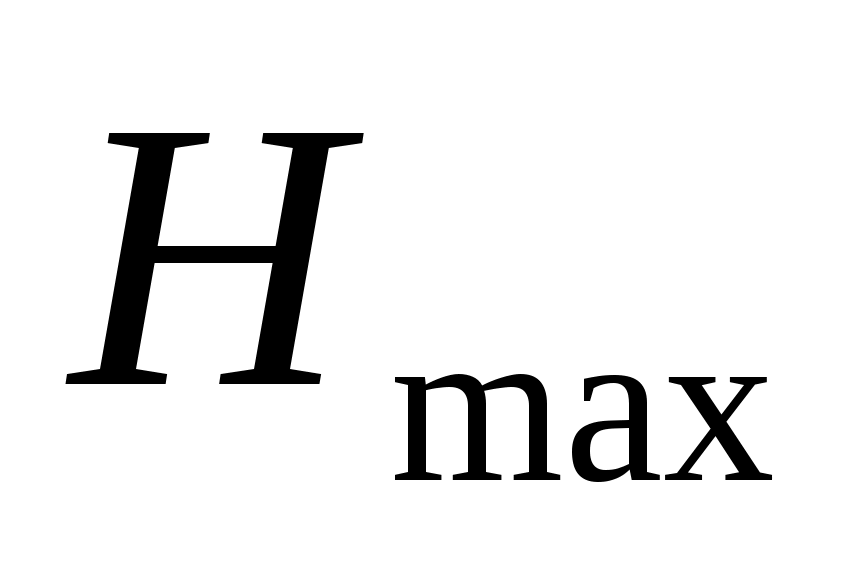 – максимальное значение энтропии, – максимальное значение энтропии, 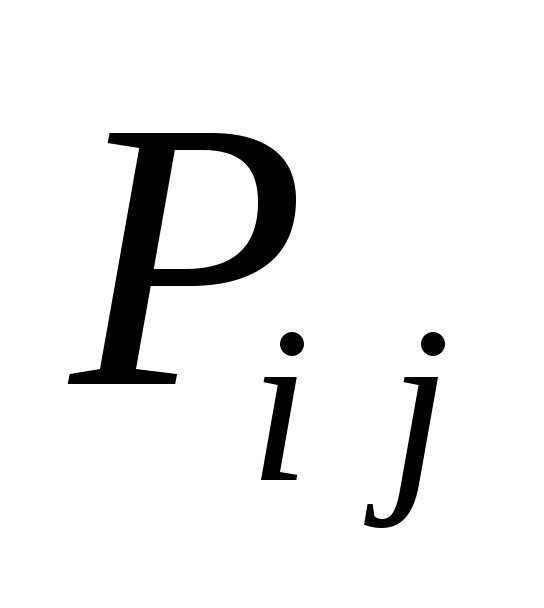 – оценки вероятности присвоения – оценки вероятности присвоения 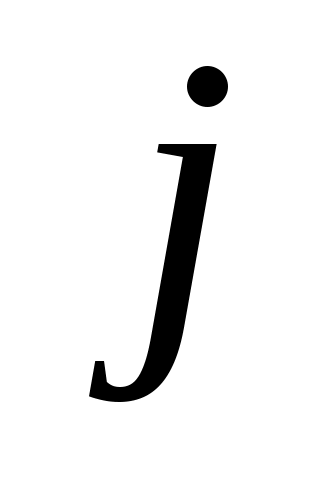 -го ранга -го ранга 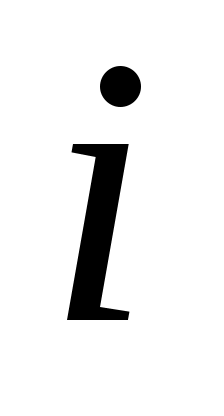 -му объекту. Эти оценки вероятностей вычисляются в виде отношения количества экспертов -му объекту. Эти оценки вероятностей вычисляются в виде отношения количества экспертов 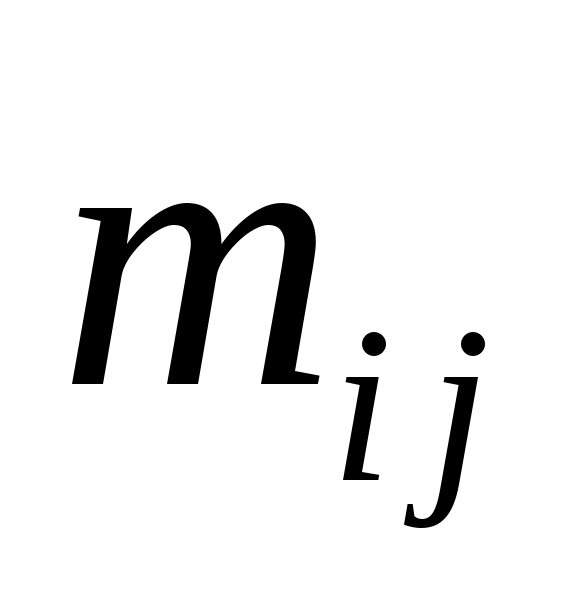 , приписавших альтернативе , приписавших альтернативе  ранг ранг 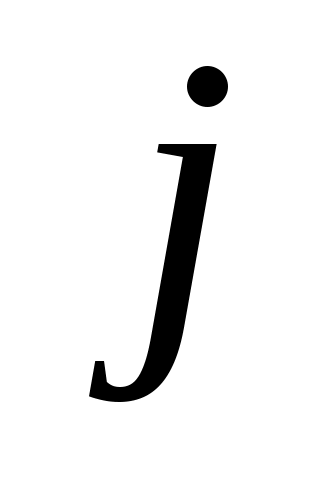 , к общему числу экспертов , к общему числу экспертов 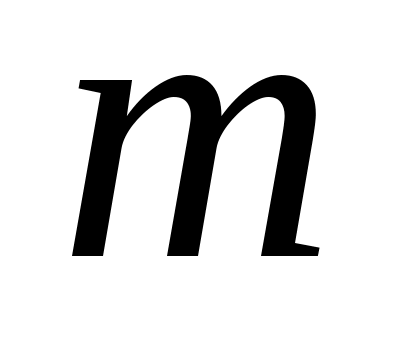 : :
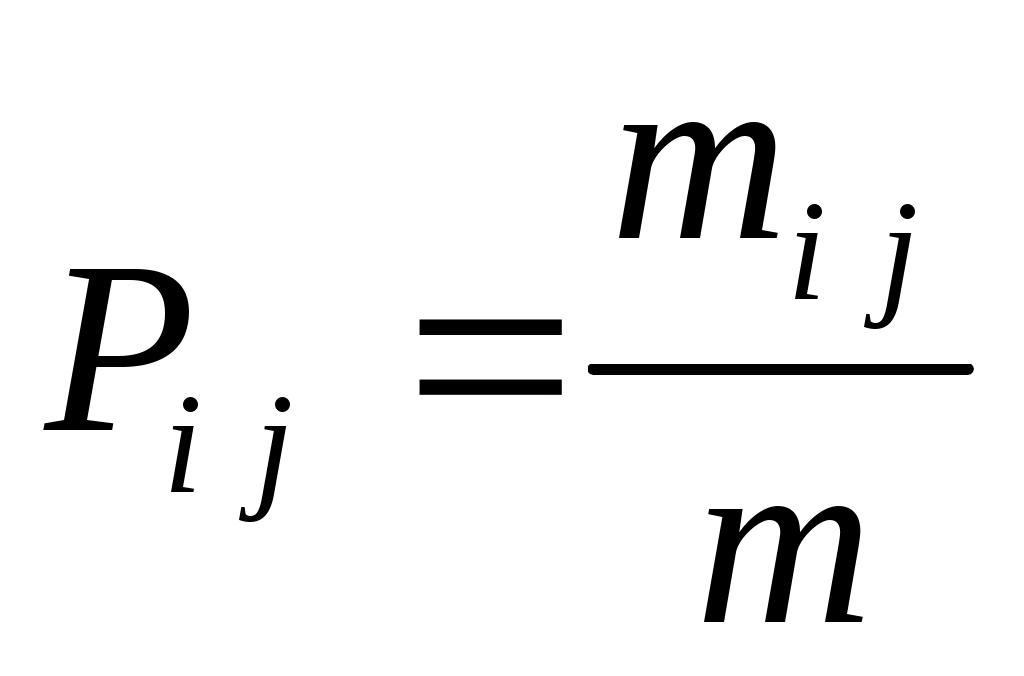 . .
Максимальное значение энтропии достигается при равновероятном распределении рангов, т. е. когда 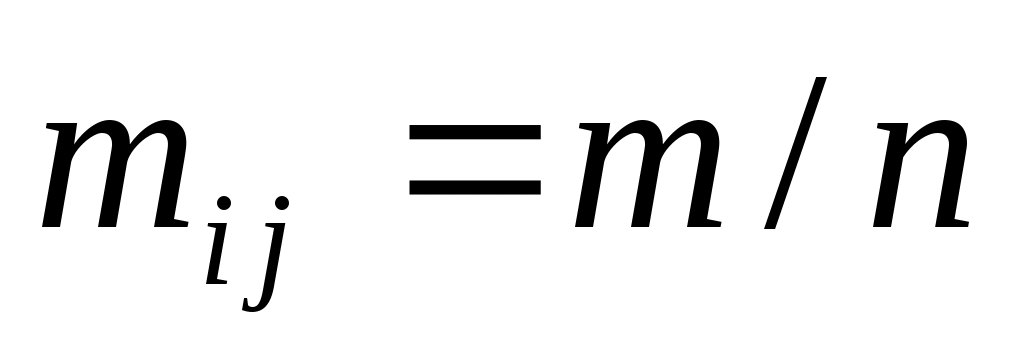 . Тогда . Тогда
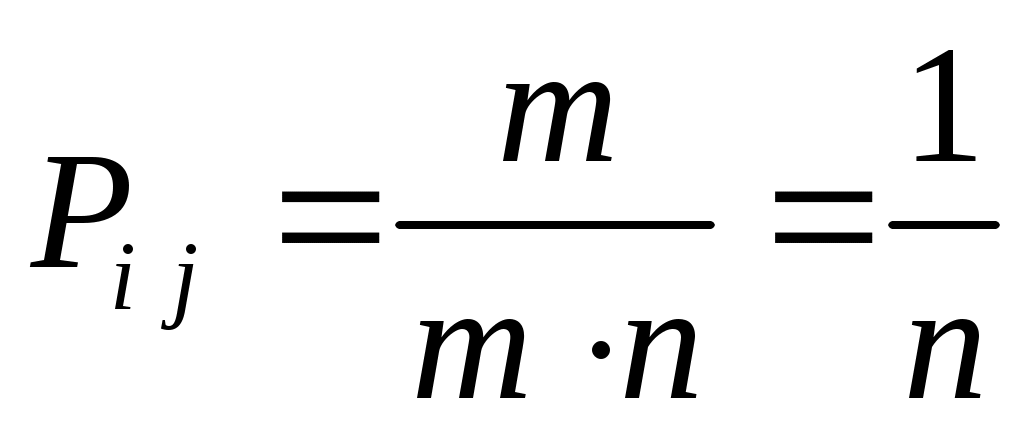 . .
Подставляя это соотношение в формулу (2.12), получаем:
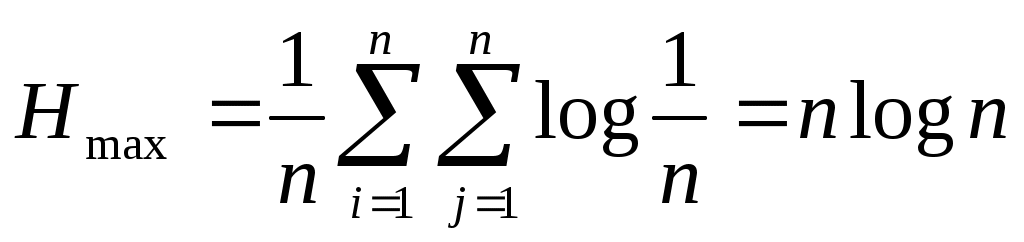 . .
Значения энтропийного коэффициента конкордации согласия изменяются в интервале: 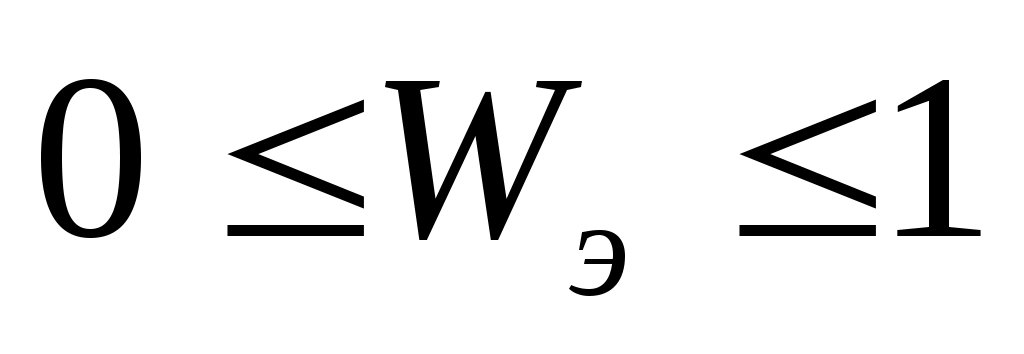 . При . При 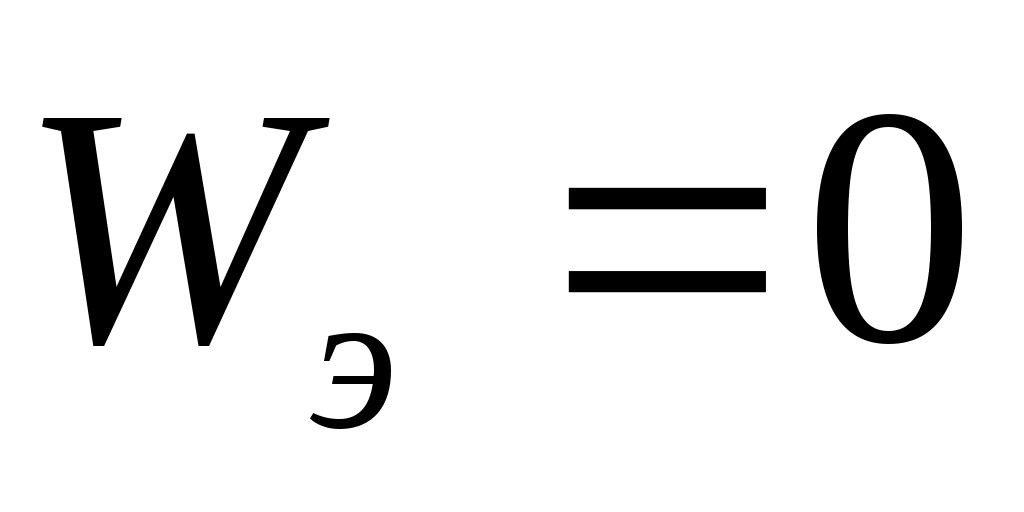 распределение альтернатив по рангам равновероятно, поскольку в этом случае распределение альтернатив по рангам равновероятно, поскольку в этом случае 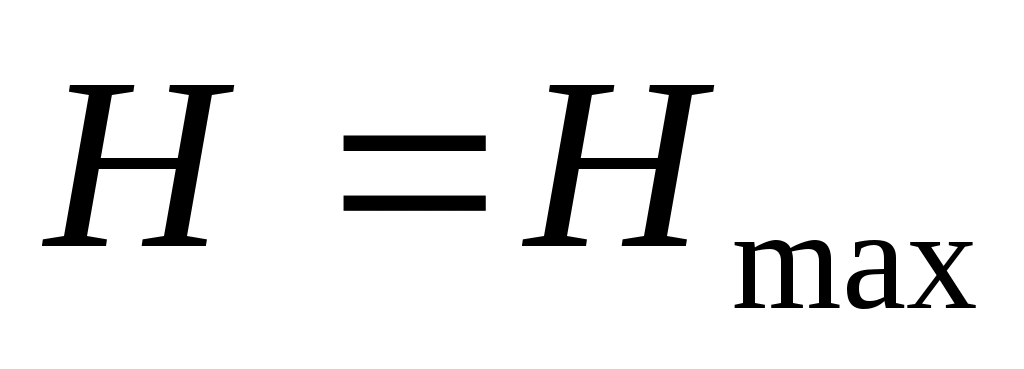 . Данный случай может быть обусловлен либо невозможностью ранжировки объектов по сформулированной совокупности показателей, либо полной несогласованностью мнений экспертов. Значение . Данный случай может быть обусловлен либо невозможностью ранжировки объектов по сформулированной совокупности показателей, либо полной несогласованностью мнений экспертов. Значение 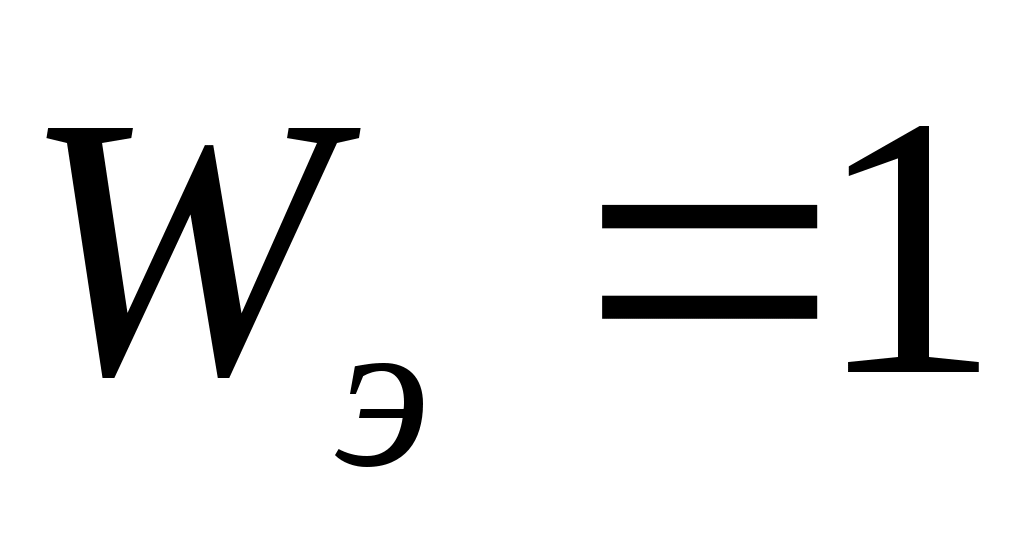 достигается при достигается при 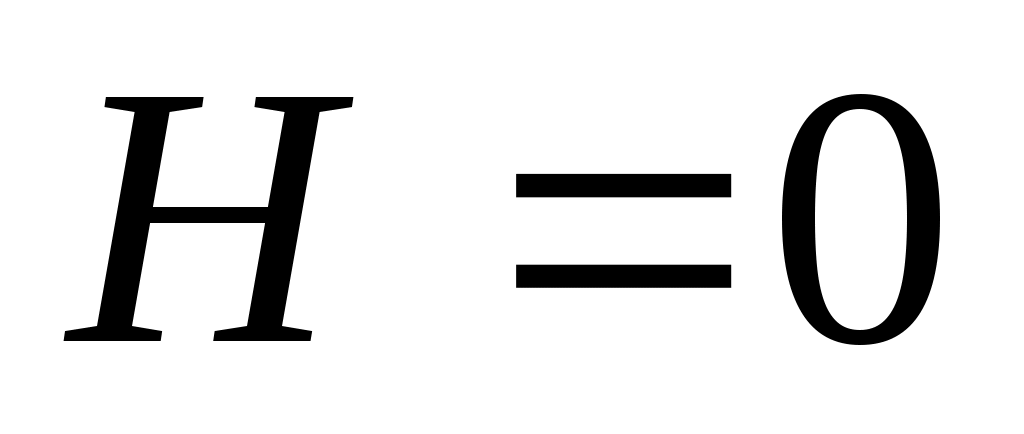 , когда все эксперты дают одинаковую ранжировку. , когда все эксперты дают одинаковую ранжировку.
Сравнительная оценка дисперсионного и энтропийного коэффициентов конкордации показывает, что эти коэффициенты дают примерно одинаковую оценку согласованности мнений экспертов при близких ранжировках. Однако, если, например, вся группа экспертов разделилась на подгруппы, причем ранжировки в этих подгруппах противоположные, то коэффициенты конкордации имеют разные значения. В таких случаях энтропийный коэффициент конкордации позволяет зафиксировать факт разделения мнений на противоположные группы. Объем вычислений для энтропийного коэффициента конкордации несколько больше, чем для дисперсионного коэффициента конкордации.
|
 Скачать 0.92 Mb.
Скачать 0.92 Mb.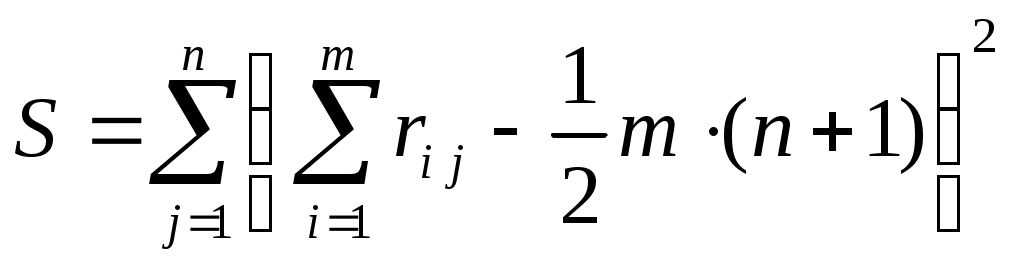 ,
,