Экспертные оценки. Тема 2 Экс. оценки-1 (1). Тема экспертные оценки. Методы и применение
 Скачать 0.92 Mb.
|
|
2.7. Методы обработки экспертной информации, оценка компетентности и согласованности мнений экспертов Наличие как числовых данных, так и содержательных высказываний экспертов приводит к необходимости применения количественных и качественных методов обработки результатов экспертного оценивания. Для обработки результатов группового экспертного оценивания проблемы, для решения которой имеется необходимый информационный потенциал (достаточный уровень знаний и опыта), можно применять методы математической статистики, основанные на осреднении данных. В зависимости от целей экспертного оценивания и выбранного метода опроса при обработке результатов опроса возникают следующие задачи: – построение обобщенной оценки альтернатив на основе индивидуальных оценок экспертов; – построение обобщенной оценки на основе парного сравнения альтернатив каждым экспертом; – определение относительных весов альтернатив; – определение согласованности мнений экспертов; – определение зависимостей между ранжировками; – оценка надежности результатов обработки. Задача построения обобщенной оценки альтернатив по индивидуальным оценкам экспертов возникает при групповом экспертном оценивании. Решение этой задачи зависит от использованного экспертами метода измерения. Рассмотрим алгоритмы обработки результатов экспертного оценивания множества альтернатив. Пусть  экспертов произвели оценку  альтернатив по  показателям. Результаты оценки представим в виде величин  , где  – номер эксперта ( ), – номер альтернативы ( ),  – номер показателя (признака) сравнения. Если оценка альтернатив произведена методом ранжирования, то величины представляют собой ранги. Если оценка альтернатив выполнена методом непосредственной оценки, то величины представляют собой числа из некоторого отрезка числовой оси или баллы.Рассмотрим случай, когда величины получены методом непосредственной оценки, т. е. являются числами или баллами. Для получения групповой оценки альтернатив в этом случае можно воспользоваться средним значением оценки каждого объекта: ,  ,где  – групповая оценка -й альтернативы,  – коэффициенты весов показателей сравнения альтернатив;  – коэффициенты компетентности экспертов.Обычно используют нормированные коэффициенты весов показателей и компетентности экспертов:  ,  .Коэффициенты весов показателей могут быть определены экспертным путем. Если  – коэффициент веса -го показателя, даваемый -м экспертом, то средний коэффициент веса -го показателя по всем экспертам равен: .Коэффициенты компетентности экспертов можно вычислить по апостериорным данным, т. е. по результатам оценки альтернатив. Основной идеей этого вычисления является предположение о том, что компетентность экспертов должна оцениваться по степени согласованности их оценок с групповой оценкой объектов. Пусть экспертов оценили альтернатив, используя одну и ту же шкалу интервалов. Тогда мы имеем матрицу оценок  ,  ,  , где  – оценка -го эксперта для -го объекта.Алгоритм, предложенный Евлановым Л.Г. и Кутузовым В.А., основан на итеративной процедуре корректировки коэффициентов компетентности  ,  ,  – номер итерации. Этот алгоритм состоит из следующих основных процедур.Алгоритм 2.1 Первоначально на шаге  значения коэффициентов компетентности равны между собой:  , .Затем на шагах  коэффициенты компетентности корректируются по формулам: ,  , , ,  .Применение алгоритма 2.1 иногда дает неудовлетворительные результаты. Нами предложены новые алгоритмы, основанные на итеративной процедуре корректировки коэффициента компетентности. На каждой итерации вычисляется взвешенная групповая оценка каждой альтернативы (объекта). Затем вычисляются отклонения индивидуальных оценок экспертов от групповой оценки и коэффициенты компетентности экспертов, оценки которых близки к групповым оценкам, повышаются, а коэффициенты компетентности экспертов, оценки которых далеки от групповых оценок, понижаются. Ответ на вопрос, близко или далеко расположены оценки эксперта от групповой оценки, дает выбор нормы, описывающей расстояние между оценками. В зависимости от выбора нормы порождается соответствующий вариант алгоритма. В разработанных нами алгоритмах вычисляются специальные поправочные коэффициенты (  ) в аддитивной (алгоритм 2.2) или в мультипликативной форме (алгоритм 2.3).Алгоритмы 2.2, 2.3 1. , начальные значения коэффициентов компетентности: ,  , выбрать величины параметров  ,  ,  (например,  ,  ).2.  .3. Вычислить средние групповые оценки:  , .4. Вычислить поправочные коэффициенты, которые обратно пропорциональны норме Гельдера отклонения -го в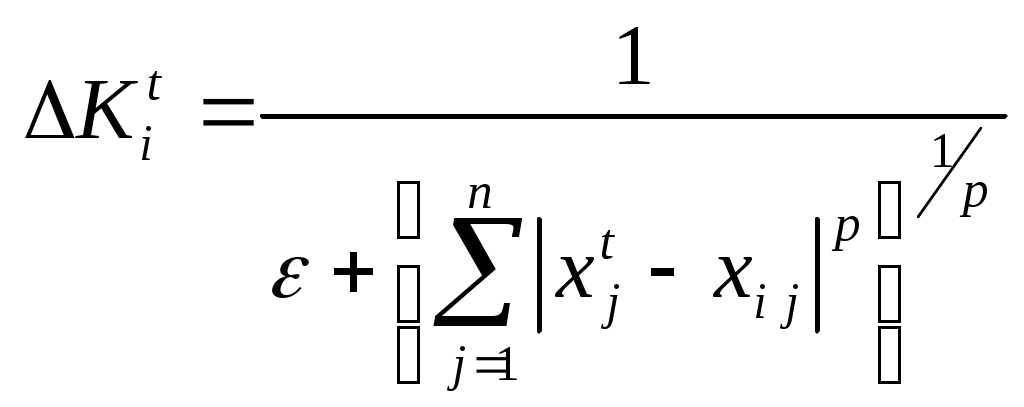ектора экспертных оценок (оценки -го эксперта) от средней групповой оценки:при   , ,  ;при 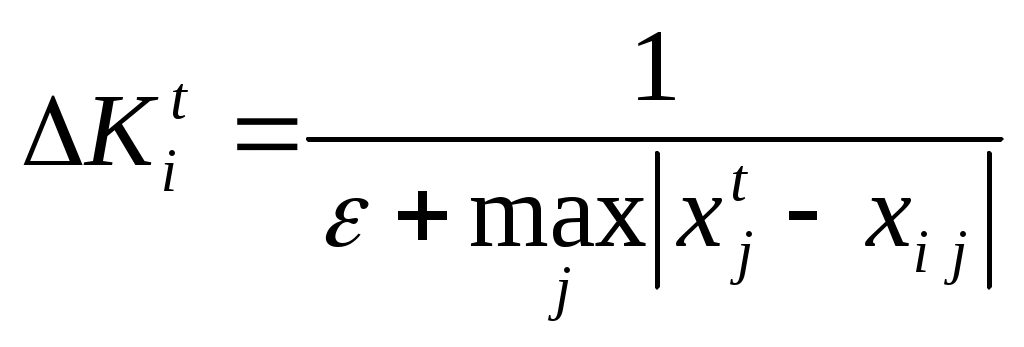  , , .5. Скорректировать коэффициенты компетентности: для аддитивного варианта – алгоритма 1.2:  , ;для мультипликативного варианта – алгоритма 1.3:  , .6. Нормализовать коэффициенты компетентности: 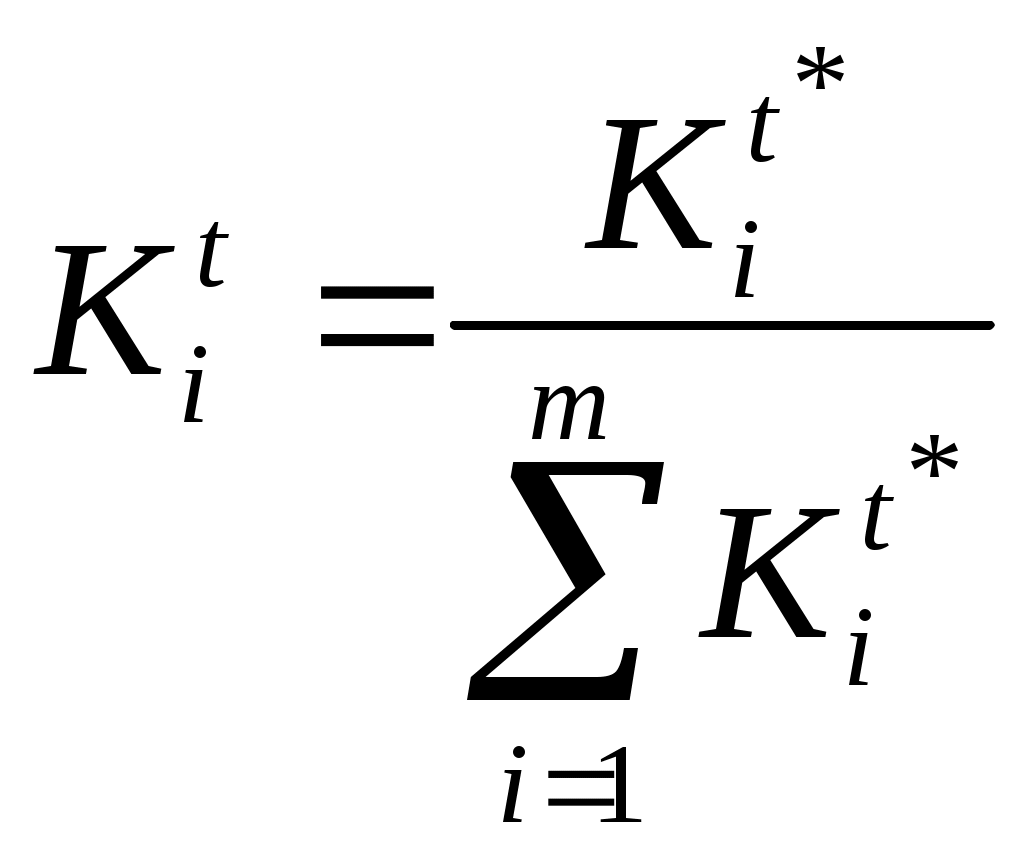 , .7. Проверить выполнение условия останова:  .Если оно выполнено, то вычисления прекратить, запомнить полученные значения коэффициентов компетентности и средние групповые оценки. Если условие останова не выполнено, то перейти к п. 2. Свойства алгоритмов 2.2, 2.3, включая их сходимость, зависят от выбора параметров и вида корректировки коэффициентов компетентности. Алгоритмы тестировались при различных и . Значения сильно влияют на скорость сходимости. С другой стороны, слишком малое приводит к слишком большому коэффициенту для наиболее компетентного эксперта при небольших коэффициентах для остальных экспертов. При очень больших все коэффициенты близки к  . Наилучшие и наиболее правдоподобные результаты в тестовых примерах получены при  . По результатам проведенного анализа можно полагать, что точность коэффициентов компетентности зависит от согласованности со шкалой индивидуальных оценок, и поэтому рекомендуется нормализовать оценки перед запуском алгоритма.Рассмотрим теперь случай, когда экспертов оценили альтернатив  , , используя одну и ту же шкалу порядка. Тогда мы имеем матрицу рангов  , , , где  – ранговая оценка -го эксперта для -й альтернативы. Обработка результатов ранжирования заключается в построении обобщенной ранжировки. Для построения такой ранжировки введем пространство ранжировок и метрику в этом пространстве. Каждая ранжировка множества альтернатив -м экспертом есть точка  в пространстве ранжировок.Ранжировку 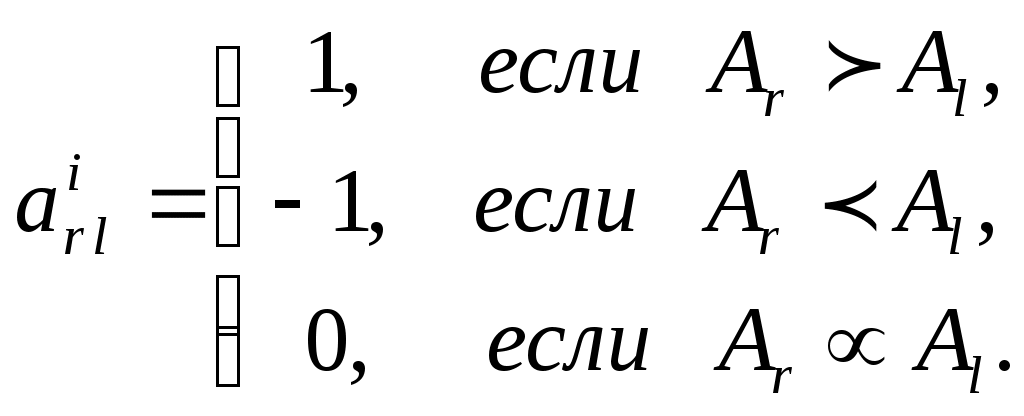можно представить в виде матрицы парных сравнений  ,  ,  , элементы которой определяется следующим образом: Очевидно, что  , т. к. каждая альтернатива эквивалентна самой себе. Элементы матрицы антисимметричны:  . Если все ранжируемые объекты эквивалентны, то все элементы матрицы парных сравнений равны нулю. Будем считать, что точка в пространстве ранжировок, соответствующая такой матрице, является началом отсчета.Метрика  при выполнении некоторых аксиом (неотрицательности, независимости от перестановок, перенумерации объектов, правило треугольника и др.) определяется по известной формуле: .Используя введенную метрику, можно определить обобщенную ранжировку как точку, которая наилучшим образом согласуется с точками, представляющими собой ранжировки экспертов. На практике наилучшее согласование чаще всего определяется как медиана или средняя ранжировка. Медиана – точка в пространстве ранжировок, сумма расстояний от которой до всех точек – ранжировок экспертов является минимальной: |