Экспертные оценки. Тема 2 Экс. оценки-1 (1). Тема экспертные оценки. Методы и применение
 Скачать 0.92 Mb.
|
 .Средняя ранжировка определяется как точка, сумма квадратов расстояний от которой до всех точек – ранжировок экспертов является минимальной:  .Если учитывается компетентность экспертов, то медиана и средняя ранжировка определяются из условий:  ,  ,где  – коэффициент компетентности  -го эксперта.Если ранжировка объектов производится по нескольким показателям, то определение медианы вначале производится для каждого эксперта по всем показателям, а затем вычисляется медиана по множеству экспертов. Основным недостатком рассмотренного выше подхода определения обобщенной ранжировки является трудоемкость расчетов. Естественный способ отыскания  или  перебором всех точек пространства ранжировок с увеличением количества объектов также становится неприемлемым, т. к. при этом очень быстро растет размерность пространства и, следовательно, объем вычислений.Расхождение обобщенных ранжировок при различных критериях возникает при малом числе экспертов и несогласованности их оценок. Если мнения экспертов близки, то обобщенные ранжировки, построенные по критериям медианы и среднего значения, будут совпадать. Сложность вычисления медианы или средней ранжировки привела к необходимости применения более простых способов построения обобщенной ранжировки. Перейдем к рассмотрению вопросов оценки согласованности мнений экспертов. При обработке результатов ранжирования часто возникает задача определения зависимости между ранжировками двух и более экспертов, задача оценки связи между достижением различных целей при решении одной и той же совокупности проблем или задача оценки взаимосвязи между различными признаками. Решение данных задач приводится с помощью оценки ранговой корреляции. Под ранговой корреляцией понимается статистическая связь между ранжировками. Данная связь анализируется на основании исходных статистических данных, представленных ранжировками  экспертов  альтернатив в виде матрицы  ,  ,  , где  – ранговая оценка -го эксперта для  -й альтернативы. Статистический анализ дает ответ на вопрос о том, есть ли какая-то согласованность (или связь) между упорядочениями анализируемых альтернатив. Рассмотрим случай оценки связи между ранжировками двух экспертов  -м и  -м экспертами ( ,  ). В этих задачах мерой взаимосвязи может служить коэффициент ранговой корреляции, например коэффициент ранговой корреляции Спирмена. Представим вычисление коэффициента ранговой корреляции Спирмена в виде следующего алгоритма. 1. Произвести ранжировки оцениваемых альтернатив двумя экспертами:  ,  ,где  ,  – векторы рангов, выставляемых соответственно -м и -м экспертами.2. Вычислить коэффициент ранговой корреляции Спирмена 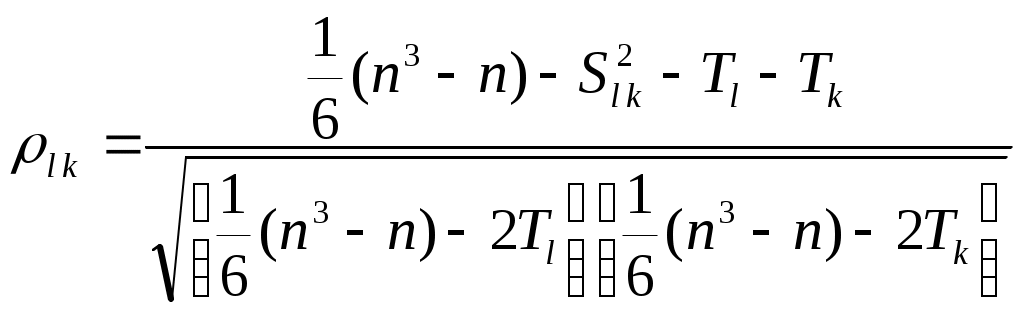 : , (2.6) ,  ,  ,где  – показатель связанных рангов в -й ранжировке;  – число групп равных рангов в -й ранжировке;  – число равных рангов в  -й группе связанных рангов в -й ранжировке.Коэффициент корреляции Спирмена изменяется от  до  . Равенство единице достигается при одинаковых ранжировках, т. е. когда  . Значение  имеет место при противоположных ранжировках. При равенстве коэффициента корреляции нулю ранжировки считаются линейно независимыми.Рассмотренный коэффициент корреляции Спирмена (2.6) является выборочной характеристикой ранговой связи. Опишем точность оценки соответствующих истинных (теоретических) значений выборочной характеристики. Поясним, что в данном случае понимается под теоретическими характеристиками. Представим себе конечную генеральную совокупность, состоящую из  альтернатив  ,  . каждая из которых снабжена двумя порядковыми номерами:  имеет номера  ,  ,  . Предполагается, что оцениваемое экспертами множество альтернатив , образуется как случайная выборка объема , взятая из генеральной совокупности альтернатив . При работе с выборкой производится естественная перенумерация альтернатив и их рангов, не меняющая их упорядоченности в генеральной совокупности.Теоретическое (истинное) значение коэффициента корреляции Спирмена вычисляется по формуле аналогичной формуле (2.6): 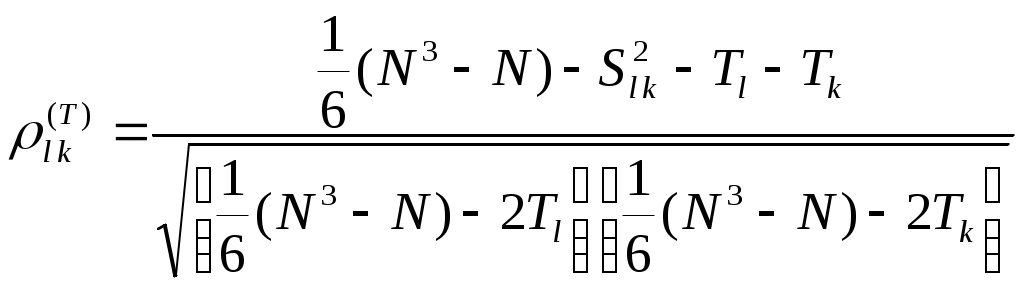 ,  , , .Проверка статистически значимого отличия от нуля рангового коэффициента корреляции проводится при «не слишком малых» 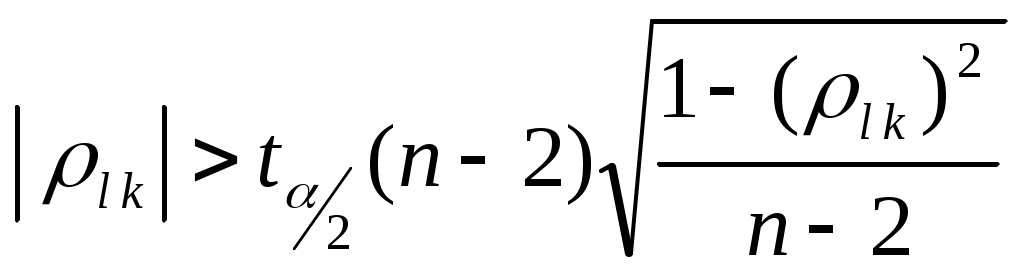( ) и заданном уровне значимости критерия  с помощью неравенства: , (2.7)где  ‑  -ная точка распределения Стьюдента с  степенями свободы,  (см.табл. 1П).Выполнение неравенства (2.7) приводит к необходимости отвергнуть гипотезу об отсутствии статистически значимой ранговой корреляционной связи. В случае небольших объемов выборок при  статистическая проверка гипотезы об отсутствии ранговой корреляционной связи производится с помощью специальных таблиц. Таблица 2П значений вспомогательной величины  позволяет при малых построить то пороговое значение  , при превышении которого по абсолютной величине коэффициентом Спирмэна  следует признать наличие статистически значимой связи между сравниваемыми ранжировками (отвергается гипотеза об отсутствии корреляционной связи). Задавшись уровнем значимости критерия и числом сравниваемых альтернатив , определяем из таблицы 2П величину  , соответствующую нашему и значению (или приблизительно равному  ). Тогда , (2.8)где  См. пример 2.4. Рассмотрим оценку согласованности мнений экспертов, когда число экспертов больше двух. В качестве меры согласованности мнений группы экспертов часто используются дисперсионный коэффициент конкордации (или согласованности) Кендалла и энтропийный коэффициент конкордации. Коэффициент конкордации Кендалла. Пусть  – матрица результатов ранжировки, полученной в результате оценки альтернатив экспертами, т. е. – ранг, присваемый -м экспертом -й альтернативе.Составим суммы рангов по каждому столбцу. В результате получим вектор с компонентами:  ,  .Величины  рассмотрим как реализации случайной величины и найдем оценку дисперсии. Как известно, оптимальная по критерию минимума среднего квадрата ошибки оценка дисперсии определяется формулой: ,где  – оценка математического ожидания, равная .Дисперсионный коэффициент конкордации определяется как отношение оценки дисперсии к максимальному значению этой оценки:  , (2.9)где  , так как  .Для случая отсутствия связанных рангов (все альтернативы разные) дисперсионный коэффициент конкордации определяется по формуле Кендалла: 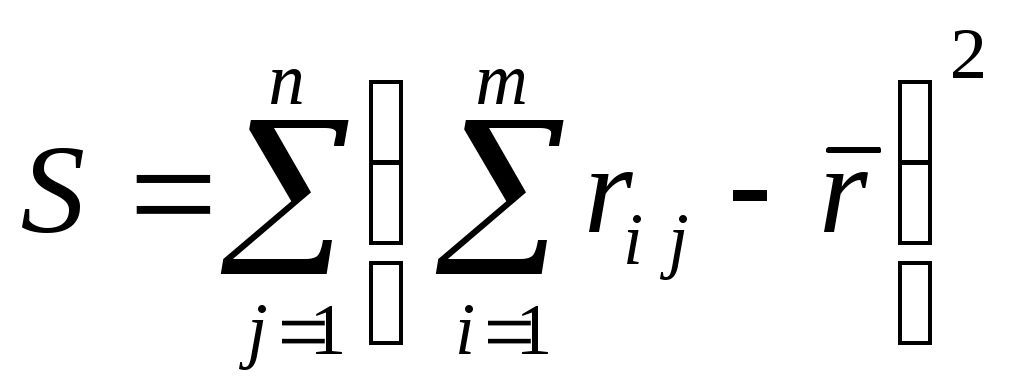 ,  . (2.10)Если в ранжировках имеются связанные ранги, то максимальное значение дисперсии в знаменателе формулы (2.10) становится меньше, чем при отсутствии связанных рангов. При наличии связанных рангов дисперсионный коэффициент конкордации вычисляется по следующей формуле: 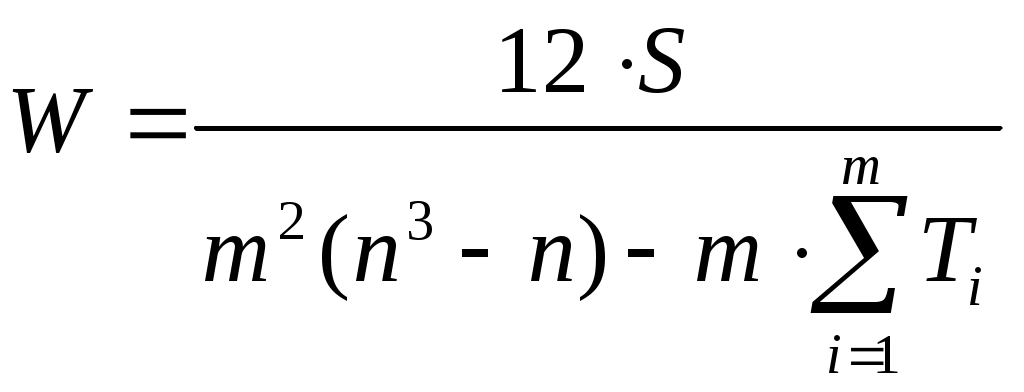 ,  (2.11)где – показатель связанных рангов в -й ранжировке; – число групп равных рангов в -й ранжировке;  – число равных рангов в -й группе связанных рангов в -й ранжировке.Если совпадающих рангов нет, то  ,  и, следовательно,  . В этом случае формула (2.11) совпадает с формулой (2.10).Коэффициент конкордации |