ответы по физике. Ответы по физике. 1. Понятие материальной точки и абсолютно твёрдого тела. Материальная точка
 Скачать 1 Mb. Скачать 1 Mb.
|
|
1.Понятие материальной точки и абсолютно твёрдого тела. Материальная точка (частица) — простейшая физическая модель в механике — обладающее массой тело, размерами, формой, вращением и внутренней структурой которого можно пренебречь в условиях исследуемой задачи. Положение материальной точки в пространстве определяется как положение геометрической точки. В классической механике масса материальной точки полагается постоянной во времени и независящей от каких-либо особенностей её движения и взаимодействия с другими телами. Абсолютно твёрдое тело - система материальных точек, расстояния между которыми не меняются в процессе движения. Реальное тело можно считать абсолютно твёрдым, если в условиях данной задачи его деформации пренебрежительно малы. 2. Путь и перемещение, скорость и ускорение - представление в прямоугольной системе координат. Путь — длина участка траектории материальной точки в физике. Перемещение(вкинематике) — изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Также перемещением называют вектор, характеризующий это изменение. Обладает свойством аддитивности. Длина отрезка — это модуль перемещения, в Международной системе единиц (СИ) измеряется в метрах. Можно определить перемещение, как изменение радиус-вектора точки: . Модуль перемещения совпадает с пройденным путём в том и только в том случае, если при движении направление скорости не изменяется. При этом траекторией будет отрезок прямой. В любом другом случае, например, при криволинейном движении, из неравенства треугольника следует, что путь строго больше. Скорость — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта; по определению, равна производной радиус-вектора точки по времени. Этим же словом называют и скалярную величину — либо модуль вектора скорости, либо алгебраическую скорость точки, т. е. проекцию этого вектора на касательную к траектории точки. Мгновенная скорость точки определяется как предел отношения перемещения к малому промежутку времени, за которое оно совершено. Более строго: В декартовых координатахВ прямоугольной декартовой системе координат: В то же время Таким образом, координаты вектора скорости — это скорости изменения соответствующей координаты материальной точки: Ускорение — физическая величина, определяющая быстроту изменения скорости тела, то есть первая производная от скорости по времени. Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени: 3. Тангенциальная и нормальная компоненты ускорения. 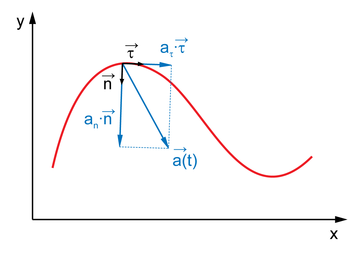 Тангенциальное ускорение — компонента ускорения, направленная по касательной к траектории движения. Характеризует изменение модуля скорости. Величину тангенциального ускорения как проекцию вектора ускорения на касательную к траектории можно выразить так: где — путевая скорость вдоль траектории, совпадающая с абсолютной величиной мгновенной скорости в данный момент. Нормальное ускорение — компонента ускорения точки, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной (вторая компонента, тангенциальное ускорение, характеризует изменение модуля скорости). Направлено к центру кривизны, также называю "центростремительным ускорением". или где — нормальное (центростремительное) ускорение, — (мгновенная) линейная скорость движения по траектории, — (мгновенная) угловая скорость этого движения относительно центра кривизны траектории, — радиус кривизны траектории в данной точке. (Связь между первой формулой и второй очевидна, учитывая ). 4. Элементарный угол поворота как вектор. Угловая скорость и угловое ускорение. Связь между линейными и угловыми характеристиками движения. Движение твердого тела, при котором две его точки О и О' остаются неподвижными, называется вращательным движением вокруг неподвижной оси, а неподвижную прямую ОО' называют осью вращения. Пусть абсолютно твердое тело вращается вокруг неподвижной оси ОО' (рис. 2.12). 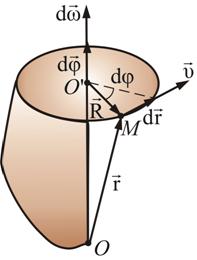 Рис. 2.12 Проследим за некоторой точкой М этого твердого тела. За время dt точка М совершает элементарное перемещение dr. При том же самом угле поворота dφ, другая точка, отстоящая от оси на большее или меньшее расстояние, совершает другое перемещение. Следовательно, ни само перемещение некоторой точки твердого тела, ни первая производная , ни вторая производная не могут служить характеристикой движения всего твердого тела. За это же время dt радиус-вектор , проведенный из точки 0' в точку М, повернется на угол dφ. На такой же угол повернется радиус-вектор любой другой точки (т.к. тело абсолютно твердое, в противном случае расстояние между точками должно измениться). Угол поворота dφ характеризует перемещение всего тела за время dt. Удобно ввести – вектор элементарного поворота тела, численно равный dφ и направленный вдоль оси вращения ОО' так, чтобы, глядя вдоль вектора, мы видели вращение по часовой стрелке (направление вектора и направление вращения связаны «правилом буравчика»). Элементарные повороты удовлетворяют обычному правилу сложения векторов: Угловой скоростью называется вектор , численно равный первой производной от угла поворота по времени и направленный вдоль оси вращения в направлении ( и всегда направлены в одну сторону).
Если ω – const, то имеет место равномерное вращение тела вокруг неподвижной оси. Пусть v – линейная скорость точки М. За промежуток времени dt точка М проходит путь dr = vdt. В то же время dr = Rdφ (dφ - центральный угол). Тогда, можно получить связь линейной скорости и угловой:
В векторной форме . Вектор ортогонален к векторам и и направлен в ту же сторону, что и векторное произведение . Наряду с угловой скоростью вращения используют понятия периода и частоты вращения. Период Т – промежуток времени, в течение которого тело совершает полный оборот (т.е. поворот на угол φ = 2π). Частота ν – число оборотов тела за 1 секунду. При вращении с угловой скоростью ω имеем: , , . Введем вектор углового ускорения для характеристики неравномерного вращения тела:
Вектор направлен в ту же сторону, что и при ускоренном вращении , а направлен в противоположную сторону при замедленном вращении 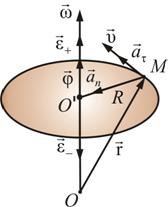 Как и любая точка твердого тела, точка М имеет нормальную и тангенциальную составляющие ускорения. Выразим нормальное и тангенциальное ускорение точки М через угловую скорость и угловое ускорение:
Обратите внимание. Все кинематические параметры, характеризующие вращательное движение (угловое ускорение, угловая скорость и угол поворота), направлены вдоль оси вращения. Формулы простейших случаев вращения тела вокруг неподвижной оси: равномерное вращение ε = 0; ω = const; φ = φ0 ± ωt, равнопеременное вращение . 5. Первый закон Ньютона. Принцип относительности Галилея. Инерциальные системы отсчёта. I закон Ньютона: Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока оно не будет выведено из этого состояния воздействием со стороны других тел. Принцип относительности Галилея: Никакими механическими опятами, проведёнными в равномерно движущейся системе, невозможно определить: двигается ил эта система или покоится. Инерциальная система отсчёта (ИСО) — система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно или покоятся. Эквивалентной является следующая формулировка, удобная для использования в теоретической механике]: «Инерциальной называется система отсчёта, по отношению к которой пространство является однородным и изотропным(если поворот системы отсчета на произвольный угол не приведет к изменению результатов измерений), а время — однородным». Законы Ньютона, а также все остальные аксиомы динамики в классической механике формулируются по отношению к инерциальным системам отсчёта. 6. Преобразования Галилея, инварианты преобразования. Преобразования Галилея — в классической механике и нерелятивистской квантовой механике преобразования координат и скорости при переходе от одной инерциальной системы отсчета (ИСО) к другой. Преобразования Галилея опираются на принцип относительности Галилея, который подразумевает одинаковость времени во всех системах отсчета («абсолютное время»). Если ИСО S' движется относительно ИСО S с постоянной скоростью вдоль оси , а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид: или, используя векторные обозначения, (последняя формула остается верной для любого направления осей координат). Как видим, это просто формулы для сдвига начала координат, линейно зависящего от времени (подразумеваемого одинаковым для всех систем отсчета). Из этих преобразований следуют соотношения между скоростями движения точки и её ускорениями в обеих системах отсчета: Уравнения, остающиеся неизменными при переходе от одной системы отсчёта к другой, называются инвариантными. 7. Второй закон Ньютона. Сила, как характеристика взаимодействия между механическими телами. Принцип линейной суперпозиции сил. Формулировка: Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует. где — ускорение тела, — сила, приложенная к телу, а — масса материальной точки. Или, в ином виде: Формулировка второго закона Ньютона с использованием понятия импульса: В инерциальных системах отсчёта производная импульса материальной точки по времени равна действующей на неё силе. где — импульс (количество движения) точки, — её скорость, а — время. Принцип суперпозиции: Результат воздействия на частицу нескольких внешних сил, есть сумма результатов воздействия каждой из них. 8.Импульс тела и импульс силы. Формулировка второго закона Ньютона. Импульс (Количество движения) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости: . Импульс служит мерой того, насколько велика должна быть сила, действующая в течении определённого времени, чтобы остановить или разогнать его с места до данной скорости. Импульс силы — это векторная физическая величина, равная произведению силы на время её действия, мера воздействия силы на тело за данный промежуток времени (в поступательном движении). За конечный промежуток времени эта величина равна определённому интегралу от элементарного импульса силы, где пределами интегрирования являются моменты начала и конца промежутка времени действия силы. В случае одновременного действия нескольких сил сумма их импульсов равна импульсу их равнодействующей за то же время. 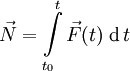 II закон Ньютона: Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует. Современная формулировка: В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки. Обычно этот закон записывается в виде формулы: где — ускорение тела, — сила, приложенная к телу, а — масса материальной точки. Или, в ином виде: Формулировка второго закона Ньютона с использованием понятия импульса: В инерциальных системах отсчёта производная импульса материальной точки по времени равна действующей на неё силе. где — импульс (количество движения) точки, — её скорость, а — время. 9. Третий закон Ньютона. Область действия законов Ньютона. Современная формулировка
Закон утверждает, что силы возникают лишь попарно, причём любая сила, действующая на тело, имеет источник происхождения в виде другого тела. Иначе говоря, сила всегда есть результат взаимодействия тел. Существование сил, возникших самостоятельно, без взаимодействующих тел, невозможно. Законы Ньютона являются основными законами механики. Из них могут быть выведены многие уравнения движения механических систем. Законы Ньютона позволяют объяснить закономерность движения планет, их естественных и искусственных спутников. В земных условиях они позволяют объяснить течение воды, движение многочисленных и разнообразных транспортных средств. 10. Силы в механике. Сила трения, сухое и вязкое трение. Класс упругих сил. Силы в механике Все многообразие встречающихся в природе взаимодействий сводится всего лишь к четырем типам. Это гравитационное электромагнитное, ядерное (или сильное) и слабое взаимодействие. В механике Ньютона можно рассматривать только гравитационное и электромагнитное взаимодействия. В отличие от короткодействующих ядерного и слабого взаимодействия, гравитационное и электромагнитное взаимодействия – дальнодействующие: их действия проявляются на очень больших расстояниях.
Сила трения Сила трения — это сила, возникающая при соприкосновении двух тел и препятствующая их относительному движению. Причиной возникновения трения является шероховатость трущихся поверхностей и взаимодействие молекул этих поверхностей. Сила трения зависит от материала трущихся поверхностей и от того, насколько сильно эти поверхности прижаты друг к другу. В простейших моделях трения считается, что сила трения прямо пропорциональна силе нормальной реакции между трущимися поверхностями. В целом же, в связи со сложностью физико-химических процессов, протекающих в зоне взаимодействия трущихся тел, процессы трения принципиально не поддаются описанию с помощью простых моделей классической механики. Разновидности силы трения При наличии относительного движения двух контактирующих тел силы трения, возникающие при их взаимодействии, можно подразделить на: Трение скольжения — сила, возникающая при поступательном перемещении одного из контактирующих/взаимодействующих тел относительно другого и действующая на это тело в направлении, противоположном направлению скольжения. Трение качения — момент сил, возникающий при качении одного из двух контактирующих/взаимодействующих тел относительно другого. Трение покоя — сила, возникающая между двумя контактирующими телами и препятствующая возникновению относительного движения. Эту силу необходимо преодолеть для того, чтобы привести два контактирующих тела в движение друг относительно друга. Возникает при микроперемещениях (например, при деформации) контактирующих тел. Она действует в направлении, противоположном направлению возможного относительного движения. сухое, когда взаимодействующие твёрдые тела не разделены никакими дополнительными слоями/смазками (в том числе и твердыми смазочными материалами) — очень редко встречающийся на практике случай. Характерная отличительная черта сухого трения — наличие значительной силы трения покоя; жидкостное (вязкое), при взаимодействии тел, разделённых слоем твёрдого тела (порошком графита), жидкости или газа (смазки) различной толщины — как правило, встречается при трении качения, когда твёрдые тела погружены в жидкость, величина вязкого трения характеризуется вязкостью среды; 11. Законы Кеплера. Закон всемирного тяготения Ньютона. Законы Кеплера — три эмпирических соотношения, интуитивно подобранных Иоганном Кеплером на основе анализа астрономических наблюдений Тихо Браге. Описывают идеализированную гелиоцентрическую орбиту планеты. В рамках классической механики выводятся из решения задачи двух тел предельным переходом / → 0, где , — массы планеты и Солнца соответственно. |
