ответы по физике. Ответы по физике. 1. Понятие материальной точки и абсолютно твёрдого тела. Материальная точка
 Скачать 1 Mb.
|
Осевой момент инерцииОсевые моменты инерции некоторых тел Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:  ,где: mi — масса i-й точки, ri — расстояние от i-й точки до оси. Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении. 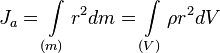 ,где: dm = ρ dV — масса малого элемента объёма тела dV, ρ — плотность, r — расстояние от элемента dV до оси a. Если тело однородно, то есть его плотность всюду одинакова, то 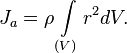 31. Вычисление момента инерции относительно данной оси. Теорема Штейнера. Теорема Гюйгенса — Штейнера (теорема Гюйгенса, теорема Штейнера): момент инерции тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:  где — известный момент инерции относительно оси, проходящей через центр масс тела, — искомый момент инерции относительно параллельной оси, — масса тела, — расстояние между указанными осями. Теорема названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса ВыводМомент инерции, по определению:  Радиус-вектор можно расписать как сумму двух векторов: , где — радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:  Вынося за сумму , получим:  Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:  Тогда:  Откуда и следует искомая формула: .32. Гироскоп, гироскопические силы, гироскопический компас, прецессия волчка. Гироскоп – массивное симметричное тело, вращающееся с большой скоростью вокруг своей оси. Если ось волчка (вращающегося) наклонена к вертикали, то волчок не падает, а совершает прецессию – его ось описывает конус вокруг вертикали с некоторой угловой скоростью ω, причем оказывается: чем больше угловая скорость вращения волчка, тем меньше угловая скорость прецессии. ГИРОСКОПИЧЕСКИЕ СИЛЫ - силы, зависящие от скоростей и обладающие тем свойством, что сумма их работ (или мощностей) при любом перемещении системы, на к-рую действуют эти силы, равна нулю. Если - Г. с., то для них  где - радиусы-векторы точек приложения сил, - скорости этих точек. Назв. "Г. с." появилось в связи с тем, что такие силы встречаются в теории гироскопа. Хотя Г. с., как зависящие от скоростей, не являются потенциальными, но на систему, на к-рую кроме потенциальных сил действуют ещё и Г. с., тоже распространяется закон сохранения механич. Энергии. Примерами Г. с. являются Кориолиса сила инерции  материально точки с массой m, движущейся со скоростью по отношению к подвижной (неинерциальной) системе отсчёта ( - угловая скорость этой системы отсчёта), и Лоренца сила  , действующая на заряж. частицу с зарядом е, движущуюся со скоростью v в магн. поле ( -магн. индукция, с - скорость света). Каждая из этих сил направлена перпендикулярно скорости, поэтому их работа или мощность при любом перемещении точки (частицы) равна нулю.33. Деформация растяжения-сжатия и сдвига. Коэффициент Пуассона. Модуль Юнга. Механические напряжения. Типовая диаграмма растяжения стержня. Сдвиг — в сопротивлении материалов — вид продольной деформации бруса, возникающий в том случае, если сила прикладывается касательно его поверхности (при этом нижняя часть бруска закреплена неподвижно). Относительная деформация сдвига определяется по формуле:  ,где Δx — абсолютный сдвиг параллельных слоёв тела относительно друг друга; l — расстояние между слоями (для малых углов ) Растяжение-сжатие — в сопротивлении материалов — вид продольной деформации стержня или бруса, возникающий в том случае, если проходит через его центр масс. |