ответы по физике. Ответы по физике. 1. Понятие материальной точки и абсолютно твёрдого тела. Материальная точка
 Скачать 1 Mb. Скачать 1 Mb.
|
Характеристики вращения телаКинематические характеристикиВращение характеризуется углом , измеряющимся в градусах или радианах, угловой скоростью (измеряется в рад/с) и угловым ускорением При равномерном вращении (T — период вращения), Частота вращения (угловая частота) — число оборотов в единицу времени. Периодвращения — время одного полного оборота. Период вращения и его частота связаны соотношением . Линейная скорость точки, находящейся на расстоянии R от оси вращения Угловая скорость вращения тела — векторная величина. Динамические характеристикиСвойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Эта характеристика входит в дифференциальные уравнения, полученные из уравнений Гамильтона или Лагранжа. Кинетическую энергию вращения можно записать в виде: В этой формуле момент инерции играет роль массы, а угловая скорость — роль скорости. Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы Момент инерциимеханической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси: где: mi — масса i-й точки, ri — расстояние от i-й точки до оси. Осевой момент инерции тела является Поворот — геометрическое преобразование. При вращении твёрдого тела относительно неподвижной оси, все точки тела движутся по плоским круговым траекториям. Выделим частицу mi тела, вращающегося вокруг оси z . Положение частицы зададим радиус-вектором относительно произвольного центра 0, лежащего на оси вращения. Ri — радиус окружности, по которой движется рассматриваемая точка. Vi = ωRi — её линейная скорость. Рассматривая твёрдое тело как неизменную систему материальных точек, для каждой из них можно записать уравнение моментов: . (9.1) В левой части этого уравнения — момент внешних сил относительно оси z, действующий на частицу mi. Справа — производная по времени проекции момента импульса частицы на ту же ось. Момент импульса частицы относительно центра 0 (по определению) равен: . Заметим, что для всех частиц , поэтому легко вычислить модуль этого вектора Li: Li = miriVi = miriωRi. 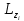 = mi = mi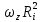 . (9.2) . (9.2)Учитывая этот результат, перепишем уравнение (9.1) ещё раз: Подобные уравнения могут быть составлены для всех точек твёрдого тела. Просуммировав все эти уравнения, получим закон вращательного движения твёрдого тела: или . (9.4) Здесь: Mz — суммарный момент всех внешних сил, вращающих твёрдое тело вокруг оси z; ωz — угловая скорость вращения; — новая характеристика твёрдого тела — его момент инерции относительно оси вращения; Lz = Izωz — момент импульса тела относительно оси z. Если момент инерции твёрдого тела Iz не меняется, уравнению (9.4) можно придать такой вид: . (9.5) Здесь ε = — угловое ускорение вращающегося тела. Уравнение (9.5) называется основным уравнением динамики для твёрдого тела, вращающегося вокруг неподвижной оси. Mz = Iz×ε (9.6)
Единица измерения в Международной системе единиц (СИ): кг·м². Обозначение: I или J. Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек. | ||||||||||
