ответы по физике. Ответы по физике. 1. Понятие материальной точки и абсолютно твёрдого тела. Материальная точка
 Скачать 1 Mb.
|
Теорема КориолисаПусть точка совершает сложное движение: движется относительно неинерциальной системы отсчёта со скоростью ; система при этом сама движется относительно инерциальной системы координат , причём линейная скорость движущегося вместе с ней полюса равна , а угловая скорость системы равна . Тогда абсолютная скорость рассматриваемой точки (то есть её линейная скорость в инерциальной системе координат) будет такой:  , причём  ,где — радиус-вектор точки относительно полюса . Первые два слагаемых в правой части равенства представляют собой переносную скорость точки, а последнее — её относительную скорость. Продифференцируем это равенство по времени:  Найдём значение каждого слагаемого в инерциальной системе координат: 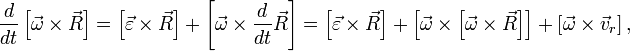   где  — линейное ускорение точки относительно системы — угловое ускорение системы .Таким образом, имеем:  Полученное равенство служит математическим выражением теоремы Кориолиса: Абсолютное ускорение точки в сложном движении равно геометрической сумме её переносного ускорения (сумма первых трёх слагаемых в правой части), относительного ускорения (четвёртое слагаемое) и добавочного кориолисова ускорения (последнее слагаемое), равного . Используя обозначения  и  , получим запись теоремы Кориолиса в более сжатом виде: Причиной возникновения кориолисова ускорения является взаимное влияние друг на друга переносного и относительного движений. 17. полный импульс механической системы, закон сохранения импульса. Определение импульса в механике НьютонаВ классической механике полным импульсом системы материальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости:  соответственно величина называется импульсом одной материальной точки. Это векторная величина, направленная в ту же сторону, что и скорость частицы. Единицей измерения импульса в Международной системе единиц (СИ) является килограмм-метр в секунду (кг·м/с). Если мы имеем дело с телом конечного размера, не состоящим из дискретных материальных точек, для определения его импульса необходимо разбить тело на малые части, которые можно считать материальными точками и просуммировать по ним, в результате получим:  Импульс системы, на которую не действуют никакие внешние силы (или они скомпенсированы), сохраняется во времени:  . (*)Сохранение импульса в этом случае следует из второго и третьего закона Ньютона: написав второй закон Ньютона для каждой из составляющих систему материальных точек и просуммировав по всем материальным точкам, составляющим систему, в силу третьего закона Ньютона получим равенство (*). 18. Понятие механической работы. Работа силы упругости. Работа силы трения. Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек), тела или системы[1] |