ответы по физике. Ответы по физике. 1. Понятие материальной точки и абсолютно твёрдого тела. Материальная точка
 Скачать 1 Mb. Скачать 1 Mb.
|
Физический смыслРассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона: — есть равнодействующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы . Учитывая, что , получим: 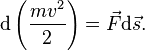 Если система замкнута, то есть внешние по отношению к системе силы отсутствуют, или равнодействующая всех сил равна нулю, то 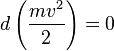 , а величина , а величинаостаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения. Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения: Физический смысл работыРабота всех сил, действующих на частицу при её перемещении, идёт на приращение кинетической энергии частицы: 21.Консервативные силы, центральные силы, потенциальная энергия. В физике консервативные силы (потенциальные силы) — это силы, работа которых не зависит от вида траектории, точки приложения этих сил и закона их движения , и определяется только начальным и конечным положением этой точки. Равносильным определением является и следующее: консервативные силы — это такие силы, работа которых по любой замкнутой траектории равна 0. В теоретической физике выделяют только четыре типа сил, каждая из которых является консервативной. В школьной программе по физике силы разделяют на консервативные и неконсервативные. Примерами консервативных сил являются: сила тяжести, сила упругости, сила кулоновского (электростатического) взаимодействия. Примером неконсервативной силы является сила трения. Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется.  Сила называется центральной, если она направлена к одной и той же точки (или от одной и той же точки) и зависит только от расстояния до этой точки, называемой центром сил или силовым центром. Пример: Сила гравитационного притяжения, с которой Солнце действует на планету. Если на систему действуют одни и те же консервативные гироскопические (зависят от скорости материальной точки и действуют всегда перпендикулярно к этой скорости) силы, то можно для неё ввести понятие потенциальной энергии. Потенциальная энергия – зависит от положения материальных точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении. Eп=mgh. 22. Полная механическая энергия механической системы, закон сохранения механической энергии. В физике механическая энергия описывает сумму потенциальной и кинетической энергий, имеющихся в компонентах механической системы. Механическая энергия — это энергия, связанная с движением объекта или его положением, имеющая способность совершать механическую работу. Сохранение механической энергииЗакон сохранения механической энергии утверждает, что если тело или система подвергается действию только консервативных сил, то полная механическая энергия этого тела или системы остаётся постоянной. В изолированной системе, где действуют только консервативные силы, полная механическая энергия сохраняется. Eполная=Eкин+Eп=const. 23. Потенциальная энергия гравитационного взаимодействия. Для двух тяготеющих точечных тел с массами M и m гравитационная энергия равна: где: — гравитационная постоянная; — расстояние между центрами масс тел. Этот результат получается из закона тяготения Ньютона, при условии, что для бесконечно удалённых тел гравитационная энергия равна 0. Выражение для гравитационной силы имеет вид где: — сила гравитационного взаимодействия С другой стороны согласно определению потенциальной энергии: Тогда: Константа в этом выражении может быть выбрана произвольно. Её обычно выбирают равной нулю, чтобы при r, стремящемуся к бесконечности, стремилось к нулю. Этот же результат верен для малого тела, находящегося вблизи поверхности большого. В этом случае R можно считать равным , где — радиус тела массой M, а h — расстояние от центра тяжести тела массой m до поверхности тела массой M. На поверхности тела M имеем: Если размеры тела много больше размеров тела , то формулу гравитационной энергии можно переписать в следующем виде: 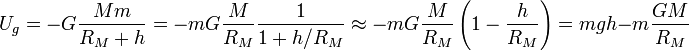 , ,где величину В частности, эта формула применяется для вычисления потенциальной энергии тел, находящихся вблизи поверхности Земли. 24(12). Изменение ускорения свободного падения с глубинной в приближении однородности земного шара. В соответствии с законом всемирного тяготения, значение гравитационного ускорения на поверхности Земли или другой планеты можно связать с массой планеты M следующим соотношением: где G — гравитационная постоянная (6,6742·10−11 м³с−2кг−1), а r — радиус планеты. Это соотношение справедливо в предположении, что планета является однородным шаром. Приведённое соотношение позволяет определить массу любой планеты, включая Землю, зная её радиус и гравитационное ускорение на её поверхности. Гравитационное ускорение на высоте h над поверхностью Земли (или другой планеты) можно вычислить по формуле: где M - масса планеты. 25. Космические скорости. Космическая скорость (первая v1, вторая v2, третья v3 и четвёртая v4) — это минимальная скорость, при которой какое-либо тело в свободном движении с поверхности небесного тела сможет: v1 (круговая скорость) — стать спутником небесного тела (то есть вращаться по круговой орбите вокруг НТ на нулевой или пренебрежимо малой высоте относительно поверхности); v2 (параболическая скорость, скорость убегания) — преодолеть гравитационное притяжение небесного тела и уйти на бесконечность; v3 — покинуть звёздную систему, преодолев притяжение звезды; v4 — покинуть галактику. Третья и четвёртая космические скорости используются редко. Вторая космическая скорость обычно определяется в предположении отсутствия каких-либо других небесных тел (например, для Луны скорость убегания равна 2,4 км/с, несмотря на то, что в действительности для удаления тела на бесконечность с поверхности Луны необходимо преодолеть притяжение Земли, Солнца и Галактики). Между первой и второй космическими скоростями существует простое соотношение: Квадрат круговой скорости (первой космической скорости) с точностью до знака равен ньютоновскому потенциалу Φ на поверхности небесного тела (при выборе нулевого потенциала на бесконечности): где M — масса планеты, R — радиус небесного тела, G — гравитационная постоянная. Квадрат скорости убегания (второй космической скорости) равен удвоенному ньютоновскому потенциалу, взятому с обратным знаком: 𝑣 2= 11,182 км/с 16,650 км/с Четвёртая космическая скорость не постоянна для всех точек галактики, а зависит от координаты. По оценкам, в районе нашего Солнца четвёртая космическая скорость составляет около 550 км/с. Значение сильно зависит не только (и не столько) от расстояния до центра Галактики, но и от распределения масс вещества по Галактике, о которых пока нет точных данных, ввиду того что видимая материя составляет лишь малую часть общей гравитирующей массы, а все остальное — скрытая масса. Вне диска Галактики распределение масс приблизительно сферически симметрично, как следует из измерений скоростей шаровых скоплений и других объектов сферической подсистемы. Четвертая космическая скорость численно равна квадратному корню из гравитационного потенциала в данной точке галактики (если выбрать гравитационный потенциал равным нулю на бесконечности): , где φ — гравитационный потенциал. 26. Понятие удара. Абсолютно упругое, абсолютно неупругое и не вполне упругое соударение с позиции законов сохранения. Уда́р — толчoк, кратковременное взаимодействие тел, при котором происходит перераспределение кинетической энергии. Часто носит разрушительный для взаимодействующих тел характер. В физике под ударом понимают такой тип взаимодействия движущихся тел, при котором временем взаимодействия можно пренебречь. Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется. В классической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно. Хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков. Для математического описания простейших абсолютно упругих ударов используется закон сохранения энергии и закон сохранения импульса. Здесь m1, m2 — массы первого и второго тел. u1, v1 — скорость первого тела до, и после взаимодействия. u2, v2 — скорость второго тела до, и после взаимодействия. Важно — импульсы складываются векторно, а энергии скалярно. Абсолю́тно неупру́гий удар — удар, в результате которого компоненты скоростей тел, нормальные площадке касания, становятся равными. Если удар был центральным (скорости были перпендикулярны касательной плоскости), то тела соединяются и продолжают дальнейшее своё движение как единое тело. Где v это общая скорость тел, полученная после удара, ma - масса первого тела, ua - скорость первого тела до соударения. mb - масса второго тела, ub -скорость второго тела до соударения. Важно - импульсы являются величинами векторными, поэтому складываются только векторно. Как и при любом ударе, при этом выполняются закон сохранения импульса и закон сохранения момента импульса, но не выполняется закон сохранения механической энергии. Часть кинетической энергии соударяемых тел в результате неупругих деформаций переходит в тепловую. Хорошая модель абсолютно неупругого удара — сталкивающиеся пластилиновые шарики. Не вполне упругий удар — лишь часть энергии упругой деформации переходит в кинетическую энергию движения . Ньютон предложил характеризовать не вполне упругий удар так называемым коэффициентом восстановления. Он равен отношению скоростей взаимодействующих тел после и до удара. Коэффициент восстановления можно измерить так: сбросить мяч на жесткую горизонтальную поверхность, измерить высоту падения мяча ( 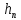 ) и высоту, на которую он отскакивает ( ) и высоту, на которую он отскакивает (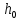 ). Коэффициент восстановления равен: ). Коэффициент восстановления равен:K= 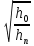 = =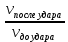 27. Момент импульса системы материальных тел. Результирующий момент сил. Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение. Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях). |
