ответы по физике. Ответы по физике. 1. Понятие материальной точки и абсолютно твёрдого тела. Материальная точка

• Название: 1. Понятие материальной точки и абсолютно твёрдого тела. Материальная точка
• Анкор: ответы по физике
• Дата: 26.01.2022
• Размер: 1 Mb.
• Имя файла: Ответы по физике.docx
• Тип: Документы; #343098
• страница: 14 из 14

Энергия волны

При распространении волны в пространстве от какого-либо источника происходит и распространение энергии; частицы среды, вовлекаемые в колебательное движение, получают энергию от волны. Проследим, как энергия от источника распространяется в пространстве.

Предположим, что наш источник - плоская металлическая мембрана, колеблющаяся с определённой частотой. Колебаться мембрану заставляет вынуждающая сила, в данном случае - переменное (синусоидальное) магнитное поле. Мембрана, в свою очередь, заставляет колебаться частицы воздуха, и в пространстве за мембраной распространяется плоская продольная упругая волна.

Энергия мембраны есть энергия её движения, то есть чисто кинетическая энергия. (Мы полагаем мембрану безинерционной и неупругой, её колебания в точности соответствуют колебаниям магнитного поля.) Среду, в которой распространяется волна (воздух) будем считать идеальной, не поглощающей волну (реально это справедливо для небольших участков пространства, в пределах которых диссипацией энергии можно пренебречь).

Поскольку мембрана колеблется по синусоидальному закону, её энергия (кинетическая) также будет периодически меняться со временем, но с удвоенной частотой (энергия пропорциональна квадрату скорости и не зависит от её знака). Следовательно, энергия источника будет поступать в среду циклически, с частотой, в два раза большей частоты колебаний источника.

Какие формы принимает энергия в среде за мембраной? Во-первых, это кинетическая энергия частиц воздуха, пришедших в движение; во-вторых, поскольку среда упругая, это потенциальная энергия деформации воздуха. Причём и кинетическая, и потенциальная энергия в любой точке пространства изменяются абсолютно синхронно во времени: когда кинетическая энергия достигает максимума, то и потенциальная энергия максимальна, и наоборот. В самом деле, проследим за слоем воздуха непосредственно за мембраной: когда скорость мембраны максимальна, максимальна и скорость частиц воздуха, но при этом мы имеем и максимальное сжатие воздуха за мембраной. Когда скорость мембраны равна нулю (два раза за период), энергия мембраны равна нулю, в волну в эти моменты энергия не поступает.

Пусть v* - скорость частиц среды в какой-то момент времени в какой-то точке пространства (или, точнее, в физически малом объёме dV). Объёмная плотность кинетической энергии Wk запишется (r - плотность среды):

Объёмная плотность потенциальной энергии упруго деформируемой среды равна:

 - фазовая скорость волны,  - относительная деформация среды.

Учитывая, что:

имеем:



Причём в каждой точке пространства объёмные плотности кинетической и потенциальной энергий равны. Этот вывод справедлив для любых волн в упругих средах: полная механическая энергия волны в каждой точке есть сумма двух равных слагаемых, потенциальной и кинетической энергий.

Из вышеприведённой формулы следует, что среднее за период значение объёмной плотности энергии равно:

Скорость переноса энергии волной есть скорость перемещения в пространстве фиксированной амплитуды волны; для простой синусоидальной волны эта скорость совпадает с фазовой скоростью.

42. Интерференция волн. Стоячие волны.

Интерференция волн — взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга. Сопровождается чередованием максимумов (пучностей) и минимумов (узлов) интенсивности в пространстве. Результат интерференции (интерференционная картина) зависит от разности фаз накладывающихся волн.

Интерферировать могут все волны, однако устойчивая интерференционная картина будет наблюдаться только в том случае, если волны имеют одинаковую частоту и колебания в них не ортогональны. Интерференция может быть стационарной и нестационарной. Стационарную интерференционную картину могут давать только полностью когерентные волны. Например, две сферические волны на поверхности воды, распространяющиеся от двух когерентных точечных источников, при интерференции дадут результирующую волну, фронтом которой будет сфера.

При интерференции энергия волн перераспределяется в пространстве. Это не противоречит закону сохранения энергии потому, что в среднем, для большой области пространства, энергия результирующей волны равна сумме энергий интерферирующих волн.

При наложении некогерентных волн средняя величина квадрата амплитуды (то есть интенсивность результирующей волны) равна сумме квадратов амплитуд (интенсивностей) накладывающихся волн. Энергия результирующих колебаний каждой точки среды равна сумме энергий её колебаний, обусловленных всеми некогерентными волнами в отдельности. Именно отличие результирующей интенсивности волнового процесса от суммы интенсивностей его составляющих и есть признак интерференции.

Расчет результата сложения двух сферических волн

Интерференция волн от двух точечных когерентных источников. Синий — максимумы, красный/жёлтый — минимумы

Если в некоторой однородной и изотропной среде два точечных источника возбуждают сферические волны, то в произвольной точке пространства M может происходить наложение волн в соответствии с принципом суперпозиции(наложения): каждая точка среды, куда приходят две или несколько волн, принимает участие в колебаниях, вызванных каждой волной в отдельности. Таким образом волны не взаимодействуют друг с другом и распространяются независимо друг от друга.

Две одновременно распространяющиеся синусоидальные сферические волны   и  , созданные точечными источниками B₁ и B₂, вызовут в точке M колебание, которое, по принципу суперпозиции, описывается формулой  . Согласно формуле сферической волны:

,

,

где

и   — фазы распространяющихся волн

и   — волновые числа ( )

и   — циклические частоты каждой волны

и   — начальные фазы,

и   — расстояния от точки М до точечных источников B₁ и B₂

В результирующей волне 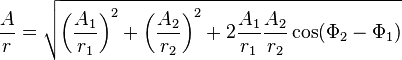 , 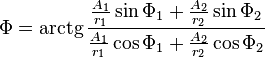амплитуда   и фаза   определяются формулами:

,




Волны и возбуждающие их источники когерентны, если разность фаз волн   не зависит от времени. Волны и разность фаз волн  изменяются с течением времени. Формула для разности фаз:

, где  , 

— скорость распространения волны в данной среде. В приведенном выше выражении от времени зависит только первый член. Две синусоидальные волны когерентны, если их частоты одинаковы ( ), и некогерентны, если условие не выполняется. Для когерентных волн ( ) при условии 

,

.

Амплитуда результирующих колебаний в любой точке среды не зависит от времени. Косинус равен единице, а амплитуда колебаний в результирующей волне максимальна   во всех точках среды, для которых  , где  (m-целое) или  , (так как  ).

Величина   называется геометрической разностью хода волн от их источников B₁ и B₂, до рассматриваемой точки среды.

Амплитуда колебаний в результирующей волне минимальна   во всех точках среды, для которых

, где   (m-натуральное),

или

.

При наложении когерентных волн квадрат амплитуды и энергия результирующей волны отличны от суммы квадратов амплитуд и суммы энергий накладываемых волн.



Стоячая волна — явление интерференции волн, распространяющихся в противоположных направлениях, при котором перенос энергии ослаблен или отсутствует.

Стоячая волна (электромагнитная) — периодическое изменение амплитуды напряженности электрического и магнитного полей вдоль направления распространения, вызванное интерференцией падающей и отраженной волн.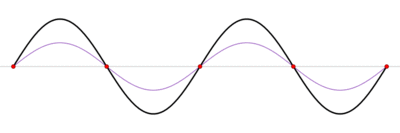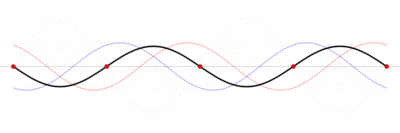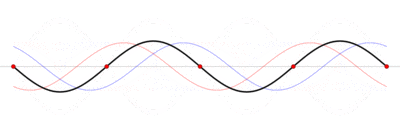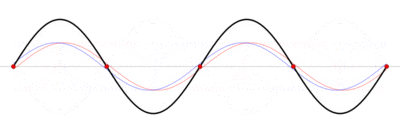



Стоячая волна — колебательный процесс в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов)амплитуды. Такой колебательный процесс возникает, например, при отражении волны от преград и неоднородностей в результате взаимодействия (интерференции) падающей и отражённой волн. На результат интерференции влияют частота колебаний, модуль и фаза коэффициента отражения, изменение или сохранение поляризации волн при отражении и коэффициент затухания волн в среде распространения.

Строго говоря, стоячая волна может существовать только при отсутствии потерь в среде распространения (или в активной среде) и полном отражении падающей волны. В реальной среде существует режим смешанных волн: кроме стоячей волны присутствует и Бегущая волна, переносящая энергию к местам поглощения и излучения.

Примерами стоячей волны могут служить колебания струны, колебания воздуха в органной трубе; в природе — волны Шумана. Для демонстрации стоячих волн в газе используют трубу Рубенса.


В случае гармонических колебаний в одномерной среде стоячая волна описывается формулой:

,

где u — возмущения в точке х в момент времени t,   — амплитуда стоячей волны,   — частота , k — волновой вектор,   — фаза.

Стоячие волны являются решениями волновых уравнений. Их можно представить себе как суперпозицию волн, распространяющихся в противоположных направлениях.

При существовании в среде стоячей волны, существуют точки, амплитуда колебаний в которых равна нулю. Эти точки называются узлами стоячей волны. Точки, в которых колебания имеют максимальную амплитуду, называются пучностями.