ответы по физике. Ответы по физике. 1. Понятие материальной точки и абсолютно твёрдого тела. Материальная точка

• Название: 1. Понятие материальной точки и абсолютно твёрдого тела. Материальная точка
• Анкор: ответы по физике
• Дата: 26.01.2022
• Размер: 1 Mb.
• Имя файла: Ответы по физике.docx
• Тип: Документы; #343098
• страница: 12 из 14

Затухающие колебания

Все реальные колебательные системы являются диссипативными. Энергия механических колебаний такой системы постепенно расходуется на работу против сил трения, поэтому свободные колебания всегда затухают - их амплитуда постепенно уменьшается. Во многих случаях, когда отсутствует сухое трение, в первом приближении можно считать, что при небольших скоростях движения силы, вызывающие затухание механических колебаниях, пропорциональны скорости. Эти силы, независимо от их происхождения, называют силами сопротивления.

(7.17)

где r - коэффициент сопротивления, v - скорость движения. Запишем второй закон Ньютона для затухающих колебаний тела вдоль оси ОХ 

или

(7.18)

Перепишем это уравнение в следующем виде:

и обозначим:

где   представляет ту частоту, с которой совершались бы свободные колебания системы при отсутствии сопротивления среды, т.е. при r = 0. Эту частоту называют собственной частотой колебания системы; β - коэффициент затухания. Тогда

(7.19)

Будем искать решение уравнения (7.19) в виде

где U - некоторая функция от t.

Продифференцируем два раза это выражение по времени t и, подставив значения первой и второй производных в уравнение (7.19), получим 

Решение этого, уравнения существенным образом зависит от знака коэффициента, стоящего при U. Рассмотрим случай, когда этот коэффициент положительный. Введем обозначение   тогда С вещественным ω решением этого уравнения, как мы знаем, является функция 

Таким образом, в случае малого сопротивления среды   , решением уравнения (7.19) будет функция

(7.20)

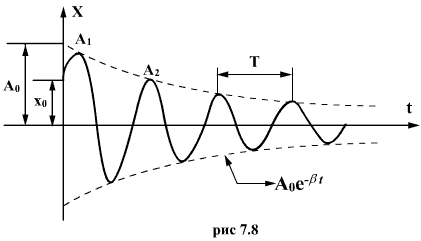График этой функции показан на рис. 7.8. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Величину   называют собственной циклической частотой колебаний диссипативной системы. Затухающие колебания представляют собой непериодические колебания, т.к, в них никогда не повторяются, например, максимальные значения смещения, скорости и ускорения. Величину   обычно называют периодом затухающих колебаний, правильнее - условным периодом затухающих колебаний,

38. Понятие декремента затухания и добротности колебательной системы для относительно слабых сил сопротивления.

Установившиеся вынужденные колебания всегда имеют такой же период, что и вызывающее их внешнее воздействие. Если это воздействие является синусоидальным, то и вынужденные колебания будут гармоническими, т е будут описываться формулой , в которой теперь ω будет равна частоте внешнего воздействия. Амплитуда А и сдвиг по фазе φ для установившихся вынужденных колебаний не зависят от начальных условий, а определяются амплитудой внешнего воздействия и соотношением между его частотой ω и частотой ω0 собственных колебаний, которые возможны в рассматриваемой системе. Зависимость А от ω носит немотонный характер. Резкое увеличение амплитуды вынужденных колебаний при приближении ω к ω0 носит название резонанса.

декремент затухания

ДЕКРЕМЕНТ ЗАТУХАНИЯ (от лат. decrementum - уменьшение, убыль) (логарифмический декремент затухания) - количественная характеристика быстроты затухания колебаний в линейной системе; представляет собой натуральный логарифм отношения двух последующих максимальных отклонений колеблющейся величины в одну и ту же сторону. T. к. в линейной системе колеблющаяся величина изменяется по закону   (где постоянная величина   - коэф. затухания) и два последующих наиб. отклонения в одну сторону X₁ и X₂ (условно наз. "амплитудами" колебаний) разделены промежутком времени  (условно наз. "периодом" колебаний), то   , а Д. з.  .

Так, напр., для механич. колебат. системы, состоящей из массы т, удерживаемой в положении равновесия пружиной с коэф.упругости k и испытывающей трение силой F_T, пропорциональной скорости v (F_Т =-bv, где b - коэф. пропорциональности), Д. з.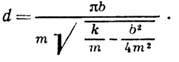



При малом затухании 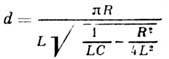  . Аналогично для электрич. контура, состоящего из индуктивности L, активного сопротивления R и ёмкости С, Д. з.

.

При малом затухании  .

Для нелинейных систем закон затухания колебаний отличен от закона   , т. е. отношение двух последующих "амплитуд" (и логарифм этого отношения) не остаётся постоянным; поэтому Д. з. не имеет такого определ. смысла, как для систем линейных.

Добротность — параметр колебательной системы, определяющий ширину резонанса и характеризующий, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.

Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.