ответы по физике. Ответы по физике. 1. Понятие материальной точки и абсолютно твёрдого тела. Материальная точка

• Название: 1. Понятие материальной точки и абсолютно твёрдого тела. Материальная точка
• Анкор: ответы по физике
• Дата: 26.01.2022
• Размер: 1 Mb.
• Имя файла: Ответы по физике.docx
• Тип: Документы; #343098
• страница: 13 из 14

Теория

Общая формула для добротности любой колебательной системы:

,

где:

• 
  — резонансная частота колебаний
  
• 
  — энергия, запасённая в колебательной системе
  
• 
  — рассеиваемая мощность.
  

Например, в электрической резонансной цепи энергия рассеивается из-за конечного сопротивления цепи, в кварцевом кристалле затухание колебаний обусловлено внутренним трением в кристалле, в объемных электромагнитных резонаторах теряется в стенках резонатора, в его материале и в элементах связи, в оптических резонаторах — на зеркалах.

Для последовательного колебательного контура в RLC цепях, в котором все три элемента включены последовательно: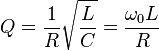

,

где  ,   и   — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно.   — частота резонанса. Выражение   часто называют характеристическим или волновым сопротивлением колебательного контура. Таким образом иное определение добротности - отношение волнового сопротивления к активному.

Для параллельного контура, в котором индуктивность, ёмкость и сопротивление включены параллельно: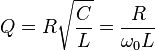

,
В данном случае   является входным сопротивлением параллельного контура. Однако, практически для электрической цепи гораздо проще измерить ток или напряжение, чем энергию или мощность. Поскольку мощность и энергия пропорциональны квадрату амплитуды колебаний, полоса частот на АЧХ будет   от пика (примерно −3 дБ, а 1/2 это −6 дБ). Поэтому чаще используется другое эквивалентное определение добротности, которое связывает ширину амплитудной резонансной кривой   по уровню   с круговой частотой резонанса  :

,

где:   — коэффициент затухания, равный полуширине резонансной кривой,   — число колебаний за время релаксации.

39. Установившиеся вынужденные колебания, резонанс.

Резонанс  — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при совпадении частоты внешнего воздействия с некоторыми значениями (резонансными частотами), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с некоторой другой частотой, определяемой из параметров колебательной системы, таких как внутренняя (собственная) частота, коэффициент вязкости и т.п. Обычно резонансная частота не сильно отличается от собственной нормальной, но далеко не во всех случаях можно говорить об их совпадении.

В результате резонанса, при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротность. При помощи резонанса можно выделить и/или усилить даже весьма слабые периодические колебания.

Механика

Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:

,

где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).

Резонансные явления могут вызвать необратимые разрушения в различных механических системах.

В основе работы механических резонаторов лежит преобразование потенциальной энергии в кинетическую. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.

Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.

Струна

Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины, массы и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, его частота зависит от скорости v, с которой волна распространяется по струне:

где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ: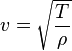



Таким образом, частота главного резонанса зависит от свойств струны и выражается следующим отношением:

,

где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.

Увеличение натяжения струны и уменьшение её массы (толщины) и длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f, и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты.

40. Волна как распространение колебаний в упругой среде. Длина волны. Скорость волны.

Волна́ — изменение некоторой совокупности физических величин (характеристик некоторого физического поля или материальной среды), которое способно перемещаться, удаляясь от места их возникновения, или колебаться внутри ограниченных областей пространства.

Волновой процесс может иметь самую разную физическую природу: механическую, химическую (реакция Белоусова — Жаботинского, протекающая в автоколебательном режиме каталитического окисления различных восстановителей бромисто-водородной кислотой HBrO₃ ), электромагнитную(электромагнитное излучение), гравитационную (гравитационные волны), спиновую (магнон), плотности вероятности (ток вероятности) и т. д. Как правило, распространение волны сопровождается переносом энергии, но не переносом массы.

Многообразие волновых процессов приводит к тому, что никаких абсолютных общих свойств волн выделить не удаётся. Одним из часто встречающихся признаков волн считается близкодействие, проявляющееся во взаимосвязи возмущений в соседних точках среды или поля, однако в общем случае может отсутствовать и оно.

Среди всего многообразия волн выделяют некоторые их простейшие типы, которые возникают во многих физических ситуациях из-за математического сходства описывающих их физических законов. Об этих законах говорят в таком случае как о волновых уравнениях. Для непрерывных систем это обычно дифференциальные уравнения в частных производных в фазовом пространстве системы, для сред часто сводимые к уравнениям, связывающим возмущения в соседних точках через пространственные и временные производные этих возмущений. Важным частным случаем волн являются линейные волны, для которых справедлив принцип суперпозиции.

По своему характеру волны подразделяются на:

• 
  По признаку распространения в пространстве: стоячие, бегущие.
  
• 
  По характеру волны: колебательные, уединённые (солитоны).
  
• 
  По типу волн: поперечные, продольные, смешанного типа.
  
• 
  По законам, описывающим волновой процесс: линейные, нелинейные.
  
• 
  По свойствам субстанции: волны в дискретных структурах, волны в непрерывных субстанциях.
  
• 
  По геометрии: сферические (пространственные), одномерные (плоские), спиральные.
  

Бегущие волны, как правило, способны удаляться на значительные расстояния от места своего возникновения (по этой причине волны иногда называют «колебанием, оторвавшимся от излучателя»).

В основном физические волны не переносят материю, но возможен вариант, где происходит волновой перенос именно материи, а не только энергии. Такие волны способны распространяться сквозь абсолютную пустоту. Примером таких волн может служить нестационарное излучение газа в вакуум, волны вероятности электрона и других частиц, волны горения, волны химической реакции, волны плотности реагентов / транспортных потоков.

Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками в пространстве, в которых колебания происходят в одинаковой фазе.

Длина́ волны́ (в линии передачи) — расстояние в линии передачи, на котором фаза электромагнитной волны вдоль направления распространения меняется на 2π^[3]

Длину волны можно также определить:

• 
  как расстояние, измеренное в направлении распространения волны, между двумя точками в пространстве, в которых фаза колебательного процесса отличается на 2π;
  
• 
  как путь, который проходит волна за интервал времени, равный периоду колебательного процесса;
  
• 
  как пространственный период волнового процесса.
  
• 
  Скорость и длина волны
  
• 
  
  Каждая волна распространяется с какой-то скоростью. Под скоростью волны понимают скорость распространения возмущения. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.
  
• 
  Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую ее скорость изменяется.
  
• 
  Помимо скорости, важной характеристикой волны является длина волны. Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.
  
• 
  Направление распространения воины
  
• 
  Поскольку скорость волны - величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на периодколебаний в ней: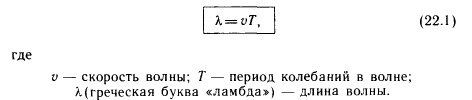
  
  Выбрав направление распространения волны за направление оси х и обозначив через у координату колеблющихся в волне частиц, можно построить график волны. График синусоидальной волны (при фиксированном времени t) изображен на рисунке 45.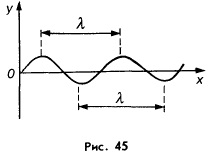
  
  Расстояние между соседними гребнями (или впадинами) на этом графике совпадает с длиной волны.
  
• 
  Формула (22.1) выражает связь длины волны с ее скоростью и периодом. Учитывая, что период колебаний в волне обратно пропорционален частоте, т.е. Т=1/v, можно получить формулу, выражающую связь длины волны с ее скоростью и частотой: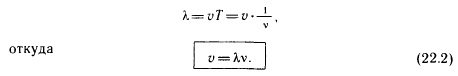
  
  Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
  
• 
  Частота колебаний в волне совпадает с частотой колебаний источника (так как колебания частиц среды являются вынужденными) и не зависит от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
  

41. Энергия волны в упругой среде.