ответы по физике. Ответы по физике. 1. Понятие материальной точки и абсолютно твёрдого тела. Материальная точка
 Скачать 1 Mb. Скачать 1 Mb.
|
Момент импульса в классической механике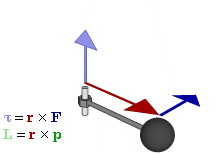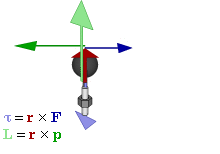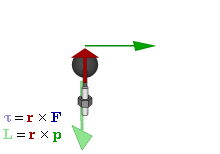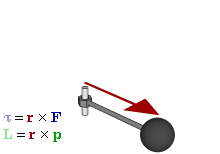 Связь между силой F, моментом силы τ, импульсом и моментом импульса ОпределениеМомент импульса материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса: где — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, — импульс частицы. Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов: где — радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется. (В пределе количество частиц может быть бесконечным, например, в случае твердого тела с непрерывно распределенной массой или вообще распределенной системы это может быть записано как В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с. Из определения момента импульса следует его аддитивность: как, для системы частиц в частности, так и для системы, состоящей из нескольких подсистем, выполняется: Замечание: в принципе момент импульса может быть вычислен относительно любого начала отсчета (получившиеся при этом разные значения связаны очевидным образом); однако чаще всего (для удобства и определенности) его вычисляют относительно центра масс или закрепленной точки вращения твердого тела и т.п.). Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению) на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов). В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ)единицей измерения момента силы является ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Более точно, момент силы частицы определяется как векторное произведение: где — сила, действующая на частицу, а — радиус-вектор частицы. 28.Проекции моментов на ось, тангенциальные силы. Основное уравнение движения в терминах моментов. (см. лекции(динамика твёрдого тела)). 29.Закон сохранения полного импульса механической системы. Закон сохранения импульса (Закон сохранения количества движения) утверждает, что векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему, равна нулю. В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил. Согласно второму закону Ньютона для системы из N частиц: где импульс системы 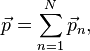 а — равнодействующая всех сил, действующих на частицы системы. Импульс системы может изменяться только под действием внешних сил, внутренние силы не могут изменить импульс системы => закон сохранения импульса системы: Импульс замкнутой системы частиц остаётся постоянным, т. е. не меняется со временем: 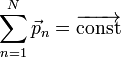 При этом импульсы отдельных частиц или частей замкнутой системы могут меняться со временем, однако эти изменения всегда происходят так, что приращение импульса одной части системы равно убыли импульса оставшейся части системы. Причина изменения импульса у незамкнутых систем – действие внешних сил. Но и незамкнутая система может сохранять импульс при условии, что результирующая всех внешних сил равна нулю. 30. Движение твёрдого тела вокруг неподвижной оси, уравнение вращательного движения в проекции на ось, момент инерции. Сферическое движение (движение твёрдого тела вокруг неподвижной точки) — движение абсолютно твёрдого тела, при котором оно имеет одну неподвижную точку. При движении вокруг неподвижной точки О каждая из точек твёрдого тела описывает в пространстве сферическую поверхность, центром которой является точка О. При описании законов сферического движения принято пользоваться координатами, получившими название углов Эйлера: — угол собственного вращения; — угол нутации. Примером сферического движения является движение прецессирующего волчка или любого тела закрученного вокруг оси, не совпадающей с осью наименьшего или наибольшего момента инерции. |
