ответы по физике. Ответы по физике. 1. Понятие материальной точки и абсолютно твёрдого тела. Материальная точка
 Скачать 1 Mb. Скачать 1 Mb.
|
ОпределениеВ механике можно ввести понятие работы, исходя из довольно простых представлений[2]. Работа силы (сил) над одной точкойРабота нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше будем говорить об одной силе. 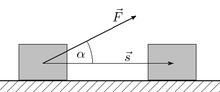 При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения[3]: Здесь точкой обозначено скалярное произведение[4], — вектор перемещения; подразумевается, что действующая сила постоянна в течение всего того времени, за которое вычисляется работа. В общем случае, когда сила не постоянна, а движение не прямолинейно, работа вычисляется как криволинейный интеграл второго рода по траектории точки[5]: (подразумевается суммирование по кривой, которая является пределом ломаной, составленной из последовательных перемещений если вначале считать их конечными, а потом устремить длину каждого к нулю). Если существует зависимость силы от координат[6], интеграл определяется[7] следующим образом: 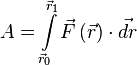 , ,где и — радиус-векторы начального и конечного положения тела соответственно. Следствие: если направление движения тела ортогонально силе, работа (этой силы) равна нулю. Работа силы упругости — работа, совершаемая силой упругости при изменении деформации пружины от некоторого начального значения x1 до конечного значения x2 Вывод формулы работы силы упругости ( через интеграл ) Коэффициент жесткости пружины k называется жесткостью тела, он зависит от материала, из которого тело изготовлено, а также от его геометрических размеров и формы. Жесткость выражается в ньютонах на метр (Н/м). Сила упругости зависит только от изменения расстояний между взаимодействующими частями данного упругого тела. Работа силы упругости не зависит от формы траектории и при перемещении по замкнутой траектории равна нулю. Поэтому силы упругости является потенциальными силами. Работа против сил трения. Е 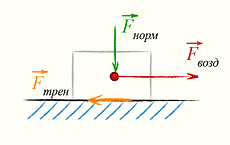 сли тело движется с постоянной скоростью (равномерно) против сил трения, то над ним совершается работа сли тело движется с постоянной скоростью (равномерно) против сил трения, то над ним совершается работа W = Fs. При этом сила F совпадает по направлению с перемещением s и равна по величине силе трения Fтр. Работа против сил трения превращается в тепловую энергию.
Здесь: W — работа против сил трения (Джоуль), Fтр — сила трения (Ньютон), μ — коэффициент трения, Fнорм — сила нормального давления (Ньютон), s — перемещение (метр), 19. Работа гравитационной силы. Пусть в точке О находится неподвижный силовой центр – материальная точка, Действующая на частицу М с силой F, которая может быть представлена в виде: F= 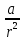 ( (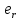 )=G )=G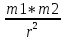 , где , где 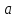 - соответствующая постоянная (G*m1*m2) - соответствующая постоянная (G*m1*m2)r  – расстояние от точки О до частицы М, – расстояние от точки О до частицы М, 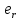 - орт радиуса-вектора r. - орт радиуса-вектора r.   dr M1 2   rr r2 1 r1 Элементарная работа этой силы на перемещение dr: ∆A=F*dr=( 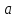 * *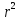 )dr* )dr*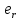 = (G = (G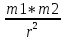 )* )*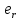 *dr *drСкалярное произведение 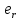 *dr=dr, т. е. приращению модуля вектора r, поэтому *dr=dr, т. е. приращению модуля вектора r, поэтому∆A= (G 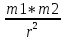 )*dr=-d*(G )*dr=-d*(G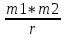 ) )Работа же этой силы на всём пути от т.1 до т.2: A=- 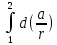 = =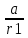 - -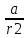 20. Понятие кинетической энергии механического тела. Кинетическая энергия — скалярная функция, являющаяся мерой движения материальной точки и зависящая только от массы и модуля скорости материальных точек, образующих рассматриваемую физическую систему, энергия механической системы, зависящая от скоростей движения её точек в выбранной системе отсчёта. Часто выделяют кинетическую энергию поступательного и вращательного движения. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением. Простым языком, кинетическая энергия - это энергия, которую тело имеет только при движении. Когда тело не движется, кинетическая энергия равна нулю. |
