|
|
ответы на комплекты. 3М и 3П ответы. Вращательное движение
3М
КОМПЛЕКТ I
1. Дайте определение вращательного движения. Назовите
кинематические параметры этого движения, их определения, единицы
измерения, связь с аналогичными параметрами поступательного
движения.
Вращательное движение – это движение, при котором все точки твердого тела движутся по концентрическим окружностям, центры которых лежат на одной прямой, называемой осью вращения.
Кинематической характеристикой направления и быстроты вращения материальной точки служит угловая скорость: 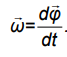
Угловая скорость ω определяется как первая производная от углового перемещения dφ по времени. Она всегда направлена так же, как и вектор углового перемещения. Единица измерения угловой скорости в СИ – с−1 . В том случае, если вектор ω меняется с течением времени, вводят понятие вектора углового ускорения ε , который характеризует быстроту изменения угловой скорости
2. Обруч массой m скатывается без проскальзывания с
наклонной плоскости с углом α = 30°. Определите ускорение его
центра масс.
См фото
3. Рассчитайте момент инерции сплошного однородного диска
массой m и радиусом r относительно оси, проходящей через середину
одного из радиусов перпендикулярно плоскости диска.
Согласно теореме Штейнера (теореме Гюйгенса-Штейнера) , момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями"
то есть момент инерции относительно центра масс. а если мы крутим тело вокруг другой оси, то момент инерции увеличивается на md^2, где m - масса тела, d - смещение от центра масс
для диска момент инерции равен 1/2*m*r^2, а в случае вращения вокруг оси на центре радиуса диска увеличивается на 1/4m*r^2, итого 3/4*m*r^2
КОМПЛЕКТ II
1. Назовите динамические характеристики вращательного движения, их определения, единицы измерения. Запишите основной закон динамики вращательного движения.
К динамическим характеристикам относятся:
· момент силы относительно точки и оси;
· момент инерции;
· момент импульса;
· импульс момента силы.
Основной закон динамики вращательного движения
(уравнение моментов) гласит: производная момента импульса тела по
времени равна векторной сумме моментов внешних сил:
dL/dt = M
Момент импульса твердого тела относительно оси равен
произведению момента инерции тела относительно той же оси на
угловую скорость:
L =J z z ⋅ω.
Для вращения тела вокруг неподвижной оси основной закон
динамики можно переписать в следующем виде:
J ⋅ ε= ∑ М.
2. По данным лабораторной работы определите момент импульса маятника Обербека чрез 3 с после начала вращения (считать, что цилиндры маятника находятся на минимальном расстоянии от оси вращения).
3. Определите момент инерции тонкого однородного стержня
длиной 50 см и массой 360 г относительно оси, перпендикулярной
стержню и проходящей через точку, отстоящую от конца стержня на
1/6 его длины.
КОМПЛЕКТ III
1. Дайте определение осевого момента инерции, приведите
примеры его значений для различных тел. Сформулируйте теорему
Штейнера.

Одно и то же тело относительно разных осей обладает различными моментами инерции. Согласно теореме Штейнера, момент инерции J тела относительно произвольной оси равен сумме его момента инерции Jc относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния d между осями
2. Шар скатывается без проскальзывания с наклонной
плоскости с углом α = 30°. Определите ускорение его центра масс.
3. Колесо вращается с постоянным угловым ускорением 3 с−2.
Определите радиус колеса, если через одну секунду после начала
движения полное линейное ускорение колеса равно 7,5 м/с2
.
КОМПЛЕКТ IV
1. Дайте определение момента силы относительно
неподвижной точки и относительно произвольной оси, проходящей
через эту точку, назовите единицы измерения момента силы.
Моментом силы M, действующим на материальную точку, относительно неподвижной точки О, называется векторное произведение радиус-вектора r на вектор силы F
Направление момента силы относительно точки О определяется по правилу правого винта Моментом импульса (моментом количества движения) материальной точки относительно неподвижной точки О называется векторное произведение радиус-вектора r на вектор импульса p этой материальной точки
Запишите основной закон динамики вращательного движения.

2. Сплошной цилиндр скатывается без проскальзывания с
наклонной плоскости с углом α = 45°. Определите ускорение его центра
масс.
3. Рассчитайте момент инерции стержня массой m, длиной L
относительно перпендикулярной ему оси, проходящей через точку О,
которая отстоит на расстоянии L/3 от конца стержня.
КОМПЛЕКТ V
1. Дайте определение вращательного движения. Назовите
кинематические параметры этого движения, их определения, единицы
измерения, связь с аналогичными параметрами поступательного
движения. См комплект 1
2. Полый тонкостенный цилиндр катится по горизонтальному
участку со скоростью 1,5 м/с2. Определить путь, который он пройдет в гору за счет своей кинетической энергии, если уклон горы равен 5 м на каждые 100 м пути.
3. Рассчитайте момент инерции шара массой m, радиусом r
относительно оси, проходящей через его край.
КОМПЛЕКТ VI
В чем заключается физическая смысл закона сохранения момента импульса? В каких системах он выполняется? Приведите примеры.
Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.
Используется гироскоп в различных навигационных устройствах кораблей, самолетов, ракет (гирокомпас, гирогоризонт). Один из примеров навигационного гироскопа Именно закон сохранения момента импульса используется танцорами на льду для изменения скорости вращения. Или еще известный пример – скамья Жуковского
2. По данным лабораторной работы определите кинетическую энергию маятника Обербека через 6 с после начала вращения (считать, что цилиндры маятника находятся на минимальном расстоянии от оси вращения).
3. Сформулируйте теорему Штейнера. Рассчитайте момент инерции диска массой m, радиусом r относительно оси, перпендикулярной плоскости диска и проходящей через его край.
Согласно теореме Штейнера (теореме Гюйгенса-Штейнера) , момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями"
то есть момент инерции относительно центра масс. а если мы крутим тело вокруг другой оси, то момент инерции увеличивается на md^2, где m - масса тела, d - смещение от центра масс
для диска момент инерции равен 1/2*m*r^2, а в случае вращения вокруг оси на краю диска увеличивается на m*r^2, итого 3/2*m*r^2
3П
I КОМПЛЕКТ
1. Электрический ток. Условия возникновения и существования
электрического тока. Сила тока. Направление. Единицы
измерения.
Электрический ток - это направленное движение электрических зарядов. В металлических проводниках, входящих в состав замкнутой электрической цепи, электрический ток создается движением электронов, направленным противоположно вектору напряженности электрического поля Е .
Сила тока ( I )- скалярная величина, равная отношению заряда q , прошедшего через поперечное сечение проводника, к промежутку времени t , в течение которого шел ток. Сила тока показывает, какой заряд проходит через поперечное сечение проводника за единицу времени.
За направление тока принимают направление движения положительно заряженных частиц; если ток создаётся отрицательно заряженными частицами (например, электронами), то направление тока считают противоположным направлению движения частиц.
Единица измерения
Сила тока в Международной системе единиц (СИ) измеряется в амперах. Ампер является одной из семи основных единиц СИ. Один ампер — это сила постоянного тока, при котором заряд, равный одному кулону проходит через поперечное сечение за одну секунду. Ампер можно также определить как силу такого тока, который при прохождении по двум параллельным прямым проводникам бесконечной длины и малого диаметра, расположенным на расстоянии 1 м друг от друга в вакууме, вызывает на участке проводника длиной 1 м силу взаимодействия, равную 0,2 мкH.
2. Сопротивление проводников. Удельное сопротивление.
Удельная проводимость. Единицы измерения.
Электрическим сопротивлением проводника, которое обозначается латинской буквой r, называется свойство тела или среды превращать электрическую энергию в тепловую при прохождении по нему электрического тока.
Сопротивление в омах проводника длиной 1 м, сечением 1 мм² называется удельным сопротивлением и обозначается греческой буквой ρ (ро)
Удельная проводимость (или удельная электролитическая проводимость) определяется, как способность вещества проводить электрический ток. Это величина, обратная удельному сопротивлению.
При химическом очищении воды очень важно измерить удельную проводимость воды, зависящую от растворенных в воде ионных соединений.
Удельная проводимость легко может быть измерена электронными приборами. Широкий спектр соответствующего оборудования позволяет сейчас измерять проводимость практически любой воды, от сверхчистой (очень низкая проводимость) до насыщенной химическими соединениями (высокая проводимость).
Основная единица измерения сопротивления - Ом. Удельная проводимость - величина обратная сопротивлению, она измеряется в Сименсах, ранее назывшихся mho. Применительно к сыпучим веществам удобнее говорить об особой проводимости, обычно называемой удельной проводимостью.
Удельная проводимость - это проводимость, измеренная между противоположными сторонами куба вещества со стороной 1 см. Единицей данного типа измерений является Сименс/см. При измерении проводимости воды чаще используются более точные мкС/см (микросименс) и мС/см (миллисименс).
3. Закон Джоуля - Ленца.
При прохождении электрического тока по проводнику он нагревается. Это происходит потому, что перемещающиеся под действием электрического поля свободные электроны в металлах и ионы в растворах электролитов сталкиваются с молекулами или атомами проводников и передают им свою энергию. Таким образом, при совершении током работы увеличивается внутренняя энергия проводника, в нём выделяется некоторое количество теплоты, равное работе тока, и проводник нагревается: Q = А или Q = IUt. Учитывая, что U = IR, в результате получаем формулу:
Q = I2Rt , где
Q — количество выделяемой теплоты (в Джоулях)
I — сила тока (в Амперах)
R — сопротивление проводника (в Омах)
t — время прохождения (в секундах)
♦ Закон Джоуля–Ленца: количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока
II КОМПЛЕКТ
1. Вектор плотности тока. Направление. Единицы измерения. Поток
вектора.
В отличие от силы тока, которая есть величина скалярная и направления не имеет, плотность тока – это вектор. Связь между этими двумя физическими величинами такова:
|

|
(7.2.1)
|
|
Модуль вектора плотности тока численно равен отношению силы тока  через элементарную площадку через элементарную площадку 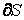 , перпендикулярную направлению движения носителей заряда, к ее площади: , перпендикулярную направлению движения носителей заряда, к ее площади:
|

|
(7.2.1)
|
|
Единица плотности тока А/м2. Плотность тока есть более подробная характеристика тока, чем сила тока I. Плотность тока характеризует ток локально, в каждой точке пространства, а I – это интегральная характеристика, привязанная не к точке, а к области пространства, в которой протекает ток.
Ясно, что плотность тока связана с плотностью свободных зарядов ρ и с дрейфовой скоростью их движения 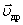 : :
|
 . .
|
(7.2.3)
|
|
За направление вектора  принимают направление вектора принимают направление вектора 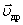 положительных носителей зарядов (раньше не знали о существовании отрицательных носителей зарядов и приняли так). Если носителями являются как положительные, так и отрицательные заряды, то плотность тока определяется формулой: положительных носителей зарядов (раньше не знали о существовании отрицательных носителей зарядов и приняли так). Если носителями являются как положительные, так и отрицательные заряды, то плотность тока определяется формулой:
|
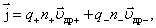
|
(7.2.4)
|
|
где  и и 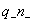 – объемные плотности соответствующих зарядов. – объемные плотности соответствующих зарядов.
Там где носители только электроны, плотность тока определяется выражением:
|

|
(7.2.5)
|
|
Поле вектора  можно изобразить графически с помощью линий тока, которые проводят так же, как и линии вектора напряженности можно изобразить графически с помощью линий тока, которые проводят так же, как и линии вектора напряженности 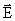 (рис. 7.1). (рис. 7.1).
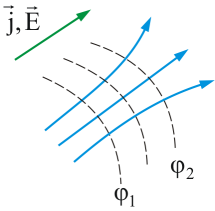
Рис. 7.1
Зная  в каждой точке интересующей нас поверхности S, можно найти силу тока через эту поверхность, как поток вектора в каждой точке интересующей нас поверхности S, можно найти силу тока через эту поверхность, как поток вектора  : :
Сила тока является скалярной величиной и алгебраической. А знак определяется, кроме всего прочего, выбором направления нормали к поверхности S.
2. Электрический заряд. Свойства электрического заряда. Закон
сохранения электрического заряда.
Электрический заряд q (далее – заряд) – скалярная характеристика тела, обладающая следующими фундаментальными свойствами:
Заряд существует в двух видах: положительный и отрицательный. Одноименные заряды отталкиваются, разноименные – притягиваются.
В природе отрицательных зарядов столько же, сколько положительных. Возникновение заряженных тел обусловлено не рождением зарядов, а их перераспределением (возникающим, например, при трении).
В СИ единица измерения заряда – Кулон: Кл[q]=Кл.
Минимальный положительный заряд равен Клe=1,6⋅10−19 Кл (элементарный заряд). Минимальный отрицательный заряд есть заряд электрона. Он равен элементарному заряду, взятому с противоположным знаком.
Величина заряда может принимать только дискретные значения, т. е. любой заряд q кратен элементарному заряду: q=N⋅e, где N – целое число.
В любой электрически изолированной системе тел алгебраическая сумма зарядов этих тел не изменяется во времени (закон сохранения заряда).
Заряд является релятивистским инвариантом – его величина не зависит от системы отсчета.
Часто в задачах мы будем работать с точечными зарядами.
Точечный заряд – заряженное тело, размерами которого можно пренебречь и считать, что весь его заряд сосредоточен в одной точке.
3. Связь между сопротивлением и проводимостью, удельным
сопротивлением и удельной проводимостью. Дать определение.
Единицы измерения.
Удельным сопротивлением называется сопротивление проводника длиной 1 м и площадью поперечного сечения 1 мм2. Удельное сопротивление обозначается буквой греческого алфавита р. Каждый материал, из которого изготовляется проводник, обладает своим удельным сопротивлением.
Например, удельное сопротивление меди равно 0,0175, т. е. медный проводник длиной 1 м и сечением 1 мм2 обладает сопротивлением 0,0175 ом.
Удельной проводимостью называется величина обратно удельному сопротивлению (гамма)
+(гамма)=1/P (Ом*м/м) , В системе СИ удельная электропроводность измеряется в сименсах.
III КОМПЛЕКТ
1. Сторонние силы. Природа сторонних сил. Электродвижущая
сила. Падение напряжения.
Для того, чтобы поддерживать ток в цепи, нужно от конца проводника с меньшим потенциалом непрерывно отводить приносимые током заряды, а к концу с большим потенциалом непрерывно их подводить. Т.е. необходимо осуществить круговорот зарядов, при котором они двигались бы по замкнутому пути. В замкнутой цепи наряду с участками, на которых положительные носители движутся в сторону убывания потенциала, должны иметься участки, на которых перенос положительного заряда происходит в направлении возрастания потенциала, т.е. против сил электростатического поля. Перемещение носителей на этих участках возможно лишь с помощью сил не электростатического происхождения, называемых сторонними силами.
Природа сторонних сил может быть различна. В генераторе на электростанции заряды разделяются действующими на них силами магнитного поля. В гальваническом элементе происходит разделение зарядов за счет энергии химической реакции и др. Величина, измеряемая работой сторонних сил Аст по перемещению единичного положительного заряда из точки 1 цепи в точку 2 для создания тока, называется электродвижущей силой (э.д.с.)  , действующей на участке 1-2 , действующей на участке 1-2  . Эта величина, в основном, используется для характеристики в источников тока (электрогенераторов, батареек, аккумуляторов), хотя в ряде явлений Э.Д.С. возникает независимо от источников. . Эта величина, в основном, используется для характеристики в источников тока (электрогенераторов, батареек, аккумуляторов), хотя в ряде явлений Э.Д.С. возникает независимо от источников.
+Сторонние силы  , действующие на заряд q0, можно записать как , действующие на заряд q0, можно записать как 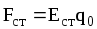 , где , где - напряженность поля сторонних сил. Учитывая, что - напряженность поля сторонних сил. Учитывая, что , получаем , получаем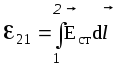 . То есть можно считать, что э.д.с., действующая в замкнутой цепи, есть циркуляция вектора напряженности поля сторонних сил . То есть можно считать, что э.д.с., действующая в замкнутой цепи, есть циркуляция вектора напряженности поля сторонних сил , гдеL - длина замкнутого контура, dl - элемент его длины. , гдеL - длина замкнутого контура, dl - элемент его длины.
Разветвление цепи. Правила Кирхгофа.
Расчет разветвленных цепей с помощью закона Ома довольно сложен. Эта задача решается более просто с помощью двух правил немецкого физика Г. Кирхгофа (1824 – 1887).
Первое правило Кирхгофа утверждает, что алгебраическая сумма токов, сходящихся в любом узле цепи равна нулю:
|

|
(7.9.1)
|
|
В случае установившегося постоянного тока в цепи ни в одной точке проводника, ни на одном из его участков не должны накапливаться электрические заряды (узел – любой участок цепи, где сходятся более двух проводников (рис. 7.8)).

Рис. 7.8
Токи, сходящиеся к узлу, считаются положительными:

Второе правило Кирхгофаявляется обобщением закона Ома для разветвленной цепи.
Для произвольного замкнутого контура с произвольным числом разветвлений (рис. 7.9) можно записать для каждого элемента контура:

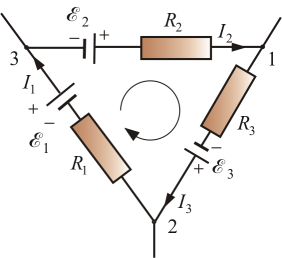
Рис. 7.9
Складывая эти уравнения получим второе правило Кирхгофа:
|

|
(7.9.2)
|
|
В любом замкнутом контуре электрической цепи алгебраическая сумма произведения тока на сопротивление равна алгебраической сумме ЭДС, действующих в этом же контуре.
Обход контуров осуществляется по часовой стрелке, если направление обхода совпадает с направлением тока, то ток берется со знаком «плюс».
Явление сверхпроводимости.
Сверхпроводимость – свойство некоторых материалов обладать абсолютно нулевым электрическим сопротивлением при достижении ими температуры ниже определённого значения (т.н. критической температуры).
Сверхпроводимостью обладают металлы и их сплавы, полупроводники, а также керамические материалы и иные вещества. Существуют даже сверхпроводящие сплавы и материалы, у которых один из элементов или все элементы, входящих в его состав, могут и не быть сверхпроводниками. Например, сероводород, славы ртути с золотом и оловом.
Сверхпроводящее состояние в материале возникает не постепенно, а скачкообразно – при достижении температуры ниже критической. Выше этой температуры металл, сплав или иной материал находится в нормальном состоянии, а ниже ее – в сверхпроводящем. Для некоторых веществ переход в сверхпроводящее состояние становится возможным при определенных внешних условиях, например, по достижении определенного значения давления.
Сверхпроводимость как явление сопровождается несколькими эффектами. Определяющее значение имеют два из них: исчезновение электрического сопротивления и выталкивание магнитного потока (поля) из его объема. Поэтому важнейшее значение приобретает не только критический ток, но и критическое магнитное поле – определенное значение напряженности магнитного поля, по достижении которого сверхпроводник теряет свойство сверхпроводимости.
Явление сверхпроводимости может быть продемонстрировано на практике. Если взять проводник, закольцевать его, сделав замкнутый электрический контур, охладить его до температуры ниже критической и подвести к нему электрический ток, а после чего убрать источник электрического тока, то электрический ток в таком проводнике будет существовать неограниченно долгое время.
IV КОМПЛЕКТ
1. Падение напряжения. Разность потенциалов. Закон Ома для
однородного участка цепи.
Первичное понятие здесь – потенциал. Электрический потенциал – это работа, которую необходимо совершить, чтобы увести заряд 1 Кл из данной точки в точку с нулевым потенциалом, то есть в точку, которая считается началом отсчёта. В электростатике за точку отсчёта обычно принимают бесконечно удалённую точку, в электронике – минусовой вывод источника питания, хотя в принципе точку отсчёта можно выбрать любую, исходя из соображений удобства. Разность потенциалов – это разность между величинами электрических потенциалов в двух точках независимо от природы того явления, которое создаёт эту разность. Она равна работе по перемещению заряда 1 Кл из одной точки в другую. ЭДС – это характеристика источника электрической энергии (гальванического элемента, батареи, генератора) . Она численно равна разности потенциалов между плюсовым и минусовым выводами источника питания на холостом ходу, то есть при отсутствии тока. Например, когда батарейка не включена в электрическую цепь. Напряжение – это разность потенциалов между выводами источника электрической энергии в рабочем режиме, т. е. когда течёт ток. Обычно оно меньше, чем ЭДС, хотя возможны исключения. Падение напряжения – это разность потенциалов, которая возникает на выводах сопротивления, когда через него течёт электрический ток. Резюме: ЭДС, напряжение, падение напряжения – это одно и то же явление, в общем случае называемое разностью потенциалов. Разница только в том, какой физический процесс порождает эту разность потенциалов.
Формула закона Ома для однородного участка цепи

Закон Ома для однородного участка цепи
I [А] – сила тока,
U [В] – напряжение,
R [Ом] – электрическое сопротивление.
Сопротивление – главная характеристика проводника. В зависимости от строения проводника, в них существует различное количество узлов кристаллической решетки и атомов примесей, взаимодействуя с которыми электроны замедляются.
2. Температурная зависимость электрического сопротивления. Как
классическая теория электропроводности металлов объясняет
зависимость сопротивления металлов от температуры.
Классическая электронная теория металлов развита Друде, Томсоном и Лоренцем. Согласно этой теории электронный газ в металле рассматривается как идеальный газ, и к нему применяют законы классической механики и статистики. В отсутствие внешнего электрического поля свободные электроны в металле совершают хаотическое тепловое движение, не создающее направленного переноса электрического заряда. При наложении электрического поля Е на каждый электрон действует сила
F = - eE,
направленная против поля и приводящая к возникновению электрического тока. Движение электрона в кристалле представляет собой сложное движение вследствие постоянного его столкновения с ионами в узлах кристаллической решетки. Между двумя актами столкновения электрон ускоряется. В конце длины свободного пробега λ под действием силы F электрон приобретает скорость направленного движения
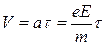 , ,
где m – масса электрона; а - его ускорение; τ – время движения электрона между двумя столкновениями. τ называется временем свободного пробега. В результате столкновения с ионом скорость электрона обращается в нуль. Поэтому средняя скорость упорядоченного движения равна:
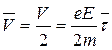 . .
Так как  , ,
то 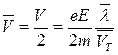 , ,
где 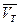 - средняя скорость теплового движения электронов. - средняя скорость теплового движения электронов.
Величина 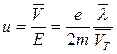 называется подвижностью. Подвижность равна скорости, приобретаемой электроном в электрическом поле, напряженность которого равна Е=1 В/м. называется подвижностью. Подвижность равна скорости, приобретаемой электроном в электрическом поле, напряженность которого равна Е=1 В/м.
В электрическом токе движение электрона является сложным движением, представляющим собой наложение хаотического теплового движения с упорядоченным движением со скоростью  в электрическом поле. Электрическое сопротивление металла обусловлено столкновением электронов с узлами кристаллической решетки и выходом их из общего потока. Чем чаще электрон сталкивается с узлами, тем выше электрическое сопротивление металла. в электрическом поле. Электрическое сопротивление металла обусловлено столкновением электронов с узлами кристаллической решетки и выходом их из общего потока. Чем чаще электрон сталкивается с узлами, тем выше электрическое сопротивление металла.
При средней скорости упорядоченного движения 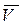 через площадку в 1 м2 , расположенную перпендикулярно к потоку, за 1 секунду пройдут все электроны, заключенные в параллелепипеде с ребром через площадку в 1 м2 , расположенную перпендикулярно к потоку, за 1 секунду пройдут все электроны, заключенные в параллелепипеде с ребром  . Объем этого параллелепипеда равен . Объем этого параллелепипеда равен  , число электронов в нем - , число электронов в нем -  , n – концентрация электронов в металле. Эти электроны перенесут заряд, равный , n – концентрация электронов в металле. Эти электроны перенесут заряд, равный 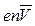 . Тогда плотность тока в проводнике будет равна . Тогда плотность тока в проводнике будет равна
 . .
Для удельной проводимости имеем
 . (1) . (1)
Подставляя в формулу (1) значение u для проводимости металла получим выражение:
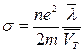 . (2) . (2)
Таким образом, согласно классической теории проводимость металла определяется средней длиной свободного пробега электрона в кристалле и средней скоростью теплового движения. Средняя длина свободного пробега 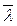 равна примерно межатомному расстоянию в решетке. Для выяснения справедливости такого предположения, оценим величину равна примерно межатомному расстоянию в решетке. Для выяснения справедливости такого предположения, оценим величину 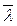 для серебра используя экспериментальные данные по проводимости. Среднюю скорость теплового движения электронов определим из соотношения: для серебра используя экспериментальные данные по проводимости. Среднюю скорость теплового движения электронов определим из соотношения:
 . .
Тогда для температуры Т300 K получим 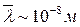 . Эта величина на два порядка больше, чем межатомное расстояние для серебра. Следовательно, экспериментальные значения проводимости металлов могут быть объяснены, если предположить, что длина свободного пробега электрона намного превышает среднее расстояние между атомами. При своем движении электрон не так часто сталкивается с ионами в узлах кристаллической решетки, как предполагает классическая теория. Прежде чем испытать столкновение электрон пролетает достаточно большое расстояние, равное, примерно 100 межатомным расстояниям в кристалле. Этот факт классическая теория не в состоянии объяснить. . Эта величина на два порядка больше, чем межатомное расстояние для серебра. Следовательно, экспериментальные значения проводимости металлов могут быть объяснены, если предположить, что длина свободного пробега электрона намного превышает среднее расстояние между атомами. При своем движении электрон не так часто сталкивается с ионами в узлах кристаллической решетки, как предполагает классическая теория. Прежде чем испытать столкновение электрон пролетает достаточно большое расстояние, равное, примерно 100 межатомным расстояниям в кристалле. Этот факт классическая теория не в состоянии объяснить.
3. Как определяется погрешность электроизмерительных приборов.
а) Нахождение абсолютной погрешности электроизмерительных приборов.
Абсолютная погрешностьэлектроизмерительных приборов определяется по классу точности приборов.
Класс точности «К» выражается в процентах и обозначается на шкале прибора соответствующей цифрой в кружке (или без него): 0,1; 0,2; 0,5;1,0; 1,5; 2,5 и 4.
Абсолютная погрешность электроизмерительных приборов определяется следующим образом:
 (2) (2)
Например, миллиамперметр 0,2 класса, шкала которого рассчитана на 75 мВ, имеет абсолютную погрешность

Если прибор многопредельный, то абсолютную погрешность требуется определить для каждого предела.
б) Нахождение относительной погрешности электроизмерительных приборов.
Относительную погрешностьопределяют по формуле:
 (2а) (2а)
Где DА- абсолютная погрешность прибора, А – значение измеряемой величины (тока или напряжения).
Так как абсолютная погрешность одинакова по всей шкале данного прибора, то относительная погрешность будет зависеть от значений измеряемой величины и тем больше, чем эта величина меньше.
Например, вольтметром, класс точности которого К=1,0 с пределом измерения 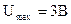 , измеряют два значения напряжения U1=0,5 В и U2=2,5 В. Относительная погрешность соответственно равна: , измеряют два значения напряжения U1=0,5 В и U2=2,5 В. Относительная погрешность соответственно равна:
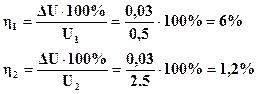
V КОМПЛЕКТ
Закон Ома для замкнутой цепи.
Закон Ома для замкнутой цепи показывает - значение тока в реальной цепи зависит не только от сопротивления нагрузки, но и от сопротивления источника.
Формулировка закона Ома для замкнутой цепи звучит следующим образом: величина тока в замкнутой цепи, состоящей из источника тока, обладающего внутренним и внешним нагрузочным сопротивлениями, равна отношению электродвижущей силы источника к сумме внутреннего и внешнего сопротивлений.
Впервые зависимость тока от сопротивлений была экспериментально установлена и описана Георгом Омом в 1826 году.
Формула закона Ома для замкнутой цепи записывается в следующем виде:
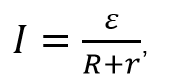
где:
I [А] – сила тока в цепи,
ε [В] – ЭДС источника напряжения,
R [Ом] – сопротивление всех внешних элементов цепи,
r [Ом] – внутреннее сопротивление источника напряжения
|
|
|
 Скачать 347.26 Kb.
Скачать 347.26 Kb.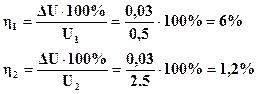
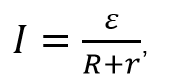

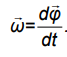







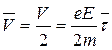 .
. ,
,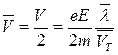 ,
,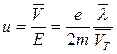 называется подвижностью. Подвижность равна скорости, приобретаемой электроном в электрическом поле, напряженность которого равна Е=1 В/м.
называется подвижностью. Подвижность равна скорости, приобретаемой электроном в электрическом поле, напряженность которого равна Е=1 В/м.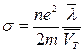 . (2)
. (2)