Коллоквиум Физика. Коллоквиум. 17. Природа носителей заряда. Классическая теория электропроводности металлов Формула Друде
 Скачать 3.24 Mb. Скачать 3.24 Mb.
|
Т . Этот и другие недостатки классической теории электропроводности металлов устранила квантовая теория электропроводности.17. Природа носителей заряда. Классическая теория электропроводности металлов 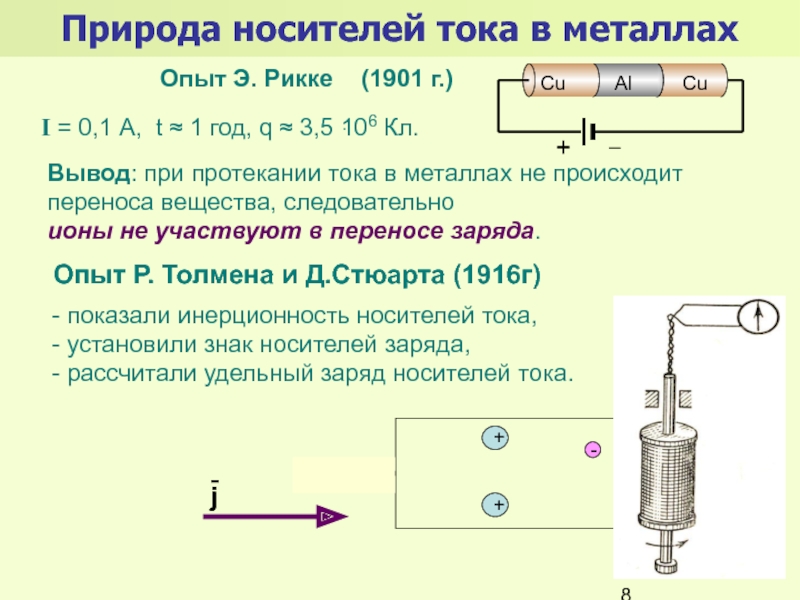 Формула Друде Формула Друде выводится из кинетического уравнения Больцмана и имеет вид: Здесь m* - эффективная масса электрона, τ - время релаксации, то есть время, за которое электрон "забывает" о том, в какую сторону двигался после соударения. Друде вывел закон Ома для токов в металле: Опыт Толмена и Стюарта В 1916 году опыт Толмена и Стюарта дал прямое доказательство тому, что носителями тока в металлах являются электроны. Суть опыта была в следующем. Опыт Толмена и Стюарта Проводящая катушка с проводом длиной L вращалась вокруг своей оси с большой скоростью, а ее концы были замкнуты на гальванометр. Когда катушку резко тормозили, свободные электроны в металле продолжали двигаться по инерции, и гальванометр регистрировал импульс тока. Считая, что свободные электроны подчиняются законам механики Ньютона, можно записать, что при остановке проводника электрон приобретает ускорение v' (в катушке направлено вдоль проводов). При этом на электрон действует сила, направленная противоположно ускорению. F=−mv' Под воздействием этой силы электрон ведет себя так, как если бы на него действовало поле считая, что ускорение одинаково в каждом витке, можно записать закон Ома для катушки, а затем вычислить заряд, проходящий в ней за время dt: 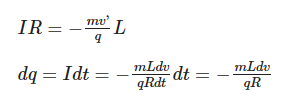 Заряд, прошедший от момента начала торможения до остановки: 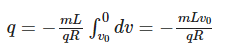 Опыт Толмена и Стюарта получил хорошее согласование с теорией, полученное экспериментально отношение q/m соответствовало отношению заряда электрона к его массе. Классическая теория электропроводности металлов Теория Друде была разработана в 1900 году, через три года после открытия электрона. Затем теория была доработана Лоренцом, и сейчас она является классической и актуальной теорией проводимости металлов. Электронная теория Друде-Лоренца Согласно теории, носителями тока в металлах являются свободные электроны Друде предположил, что электроны в металле подчиняются и могут быть описаны уравнениями молекулярно-кинетической теории. Другими словами, свободные электроны в металле подчиняются законам МКТ и образуют "электронный газ". Двигаясь в металле, электроны соударяются между собой и с кристаллической решеткой (это и есть проявление электрического сопротивления проводника). Между соударениями электроны, по аналогии с длиной свободного пробега молекул идеального газа, успевают преодолеть средний путь λ. Без действия электрического поля, ускоряющего электроны, кристаллическая решетка и электронный газ стремятся к состоянию теплового равновесия. Приведем основные положения теории Друде: Взаимодействие электрона с другими электронами и ионами не учитывается между столкновениями. Столкновения являются мгновенными событиями, внезапно меняющими скорость электрона. Вероятность для электрона испытать столкновение за единицу времени равна 1/τ. Состояние термодинамического равновесия достигается благодаря столкновениям Важно. Несмотря на множество допущений, теория Друде-Лорецна хорошо объясняет эффект Холла, явление удельной проводимости и теплопроводность металлов. Именно поэтому она актуальна по сей день, хотя ответы на многие вопросы (например, почему в металле существуют свободные ионы и электроны) смогла дать только квантовая теория твердого тела. В рамках теории Друде объясняется сопротивление металлов. Оно обусловлено соударениями электронов с узлами кристаллической решетки. Выделение тепла, согласно закону Джоуля-Ленца, также происходит по причине соударения электронов с ионами решетки. Теплопередача в металлах также осуществляется электронами, а не кристаллической решеткой. Терия Друде не объясняет многих явлений, как например сверхпроводимость, и не применима в сильных магнитных полях, в слабых магнитных полях может терять применимость из-за квантовых явлений.  Подробнее: https://zaochnik.com/spravochnik/fizika/elektrodinamika/teorija-elektroprovodnosti-metallov/ Подробнее: https://zaochnik.com/spravochnik/fizika/elektrodinamika/teorija-elektroprovodnosti-metallov/18. ЭДС источника. Разность потенциалов. Напряжение. Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних (н епотенциальных) сил висточниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура. ЭДС можно выразить через напряжённость электрического поля сторонних сил ( ). В замкнутом контуре ( ) тогда ЭДС будет равна: Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением где — поток магнитного поля через замкнутую поверхность , ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца). Электрическое напряжение между двумя точками электрической цепи или электрического поля, равно работе электрического поля по перемещению единичного положительного заряда из одной точки в другую. В потенциальном электрическом поле эта работа не зависит от пути, по которому перемещается заряд; в этом случае Э. н. между двумя точками совпадает с разностью потенциалов между ними. Если поле непотенциально, то напряжение зависит от того пути, по которому перемещается заряд между точками. Непотенциальные силы, называются сторонними, действуют внутри любого источника постоянного тока (генератора, аккумулятора, гальванического элемента и др.). Под напряжением на зажимах источника тока всегда понимают работу электрического поля по перемещению единичного положительного заряда вдоль пути, лежащего вне источника; в этом случае Э. н. равно разности потенциалов на зажимах источника и определяется законом Ома: U = IR—E, где I — сила тока, R — внутреннее сопротивление источника, а E — его электродвижущая сила (эдс). При разомкнутой цепи (I = 0) напряжение по модулю равно эдс источника. Поэтому эдс источника часто определяют как Э. н. на его зажимах при разомкнутой цепи. В случае переменного тока Э. н. обычно характеризуется действующим (эффективным) значением, которое представляет собой среднеквадратичное за период значение напряжения. Напряжение на зажимах источника переменного тока или катушки индуктивности измеряется работой электрического поля по перемещению единичного положительного заряда вдоль пути, лежащего вне источника или катушки. Вихревое (непотенциальное) электрическое поле на этом пути практически отсутствует, и напряжение равно разности потенциалов. Электродвижущая сила (ЭДС) — физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура. Наименование и обозначение производной единицы СИ: международное – volt, V русское – вольт, В Выражение через основные и производные единицы СИ: 1 V = 1 W / A 19. Закон Ома для однородного участка цепи в дифференциальной и интегральной форме. ТОК, ТЕКУЩИЙ ПО ОДНОРОДНОМУ МЕТАЛЛИЧЕСКОМУ ПРОВОДНИКУ, ПРОПОРЦИОНАЛЕН ПАДЕНИЮ НАПРЯЖЕНИЯ U НА ПРОВОДНИКЕ", т. е. I = 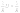 ( (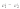 ) , (14) ) , (14) где R - сопротивление ( Ом); из (14) следует, что 1Ом =1 В/1 А. Сопротивление проводника R =ρl / S , (15) где р - удельное сопротивление, измеряется в Ом м. Оно зависит от температуры: ρ=ρ0(1+αt), где ρ0- удельное сопротивление при температуре t = 0╟С,  - температурный коэффициент сопротивления, близкий к 1/273 К - температурный коэффициент сопротивления, близкий к 1/273 К , T- термодинамическая температура ; так что с ростом температуры , T- термодинамическая температура ; так что с ростом температуры сопротивление металлических проводников увеличивается. Качественная температурная зависимость удельного сопротивления металлического проводника представлена на рис.3 Найдем связь между векторами  и и  . Для этого мысленно выделим в окрестности некоторой точки проводника элементарный цилиндрический объем с образующими, параллельными векторам . Для этого мысленно выделим в окрестности некоторой точки проводника элементарный цилиндрический объем с образующими, параллельными векторам  и и  , (см. рис. 4 ). , (см. рис. 4 ). Между концами проводника длиной dl напряжение U = Edl, под действием которого через его поперечное сечение площадью dS течет ток I = jdS. Сопротивление цилиндрического проводника, в нашем случае, равно R =  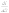 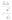 , откуда и получаем закон Ома в дифференциальной форме , откуда и получаем закон Ома в дифференциальной форме  = =   = = 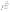 , (16) где γ= 1/ρ удельная электропроводность; [γ] = 1 / (Ом м) = 1 См / м, где 1 См = 1 / Ом - это единица измерения электропроводности в СИ, называемая сименс (См). Для металлов согласно классической теории электропроводности γ= , (16) где γ= 1/ρ удельная электропроводность; [γ] = 1 / (Ом м) = 1 См / м, где 1 См = 1 / Ом - это единица измерения электропроводности в СИ, называемая сименс (См). Для металлов согласно классической теории электропроводности γ= 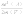 где n - концентрация свободных электронов, она может достигать 10 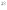  10 10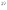 электрон / м электрон / м ; e-заряд электрона, m - его масса; < ; e-заряд электрона, m - его масса; <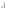 > - средняя длина свободного пробега электрона; < v > = > - средняя длина свободного пробега электрона; < v > =  (18) (18)< v > - средняя скорость теплового движения электрона, k = 1,38 10  Дж/К - постоянная Больцмана. Дж/К - постоянная Больцмана.С учетом (18) из (17) следует, что  Закон Ома для однородного участка цепи. Сила тока в однородном участке цепи прямо пропорциональна напряжению при постоянном сопротивлении участка и обратно пропорциональна сопротивлению участка при постоянном напряжении. где U- напряжение на участке, R - сопротивление участка. Закон Ома для однородного участка цепи, все точки которого имеют одинаковую температуру, выражается формулой (в современных обозначениях): В таком виде формула закона Ома справедлива только для проводников конечной длины, так как входящие в это выражение величины I и U измеряются приборами, включенными на этом участке. где Закон Ома в интегральной форме для однородного и неоднородного участков и замкнутой цепи. Закон Ома в дифференциальной форме . 2.3 Законы Ома в интегральной форме Закон Ома в интегральной форме подразумевает, что рассматривается полный ток, протекающий в цепи и величина тока со временем не меняется. Тогда закон Ома для участка цепи, содержащей э.д.с., будет иметь вид: 3) Если замкнутый участок цепи, содержит э.д.с., тогда φ1 = φ2, и получаем: В целом участок цепи, содержащей множество э.д.с. и разных деталей представлен законом Ома в виде: 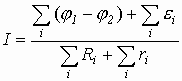 . .Из закона Ома следует: 2.3.1 Закон Ома в дифференциальной форме Сечение проводника или элементов цепи, как правило, неоднородно, и сопротивляемость в разных участках цепи протеканию тока также различная. Тогда разбивают участки цепи на элементы (дифференцируют) и определяют закон Ома в каждом отдельном участке. Учитывая, что для участка цепи и Это закон Ома в дифференциальной форме. Зная, что удельная электропроводность σ и удельное сопротивление ρ связаны, как: 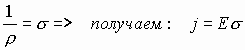 , ,где σ - удельная электропроводность, ρ - удельная сопротивление, 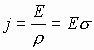 - закон Ома в дифференциальной форме. - закон Ома в дифференциальной форме.21. Последовательное и параллельное соединение проводников. Последовательное соединение проводников При последовательном соединении конец первого проводника соединяют с началом второго, конец второго — с началом третьего и т. д. 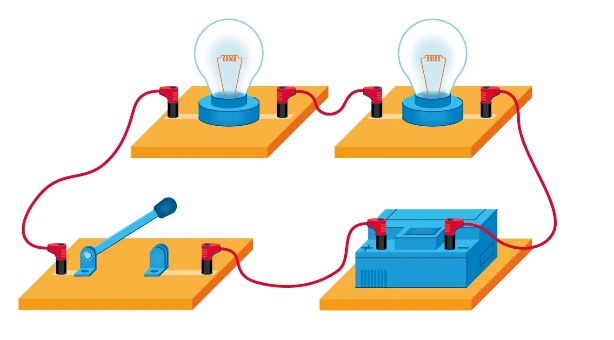 Последовательное подключение обычно используется в тех случаях, когда необходимо целенаправленно включать или выключать определенный электроприбор. Например, для работы школьного электрического звонка требуется соединить его последовательно с источником тока и ключом. Вот некоторые примеры использования схемы последовательного соединения: освещение в вагонах поезда или трамвая; простейшие елочные гирлянды; карманный фонарик; амперметр для измерения силы тока в цепи. Законы последовательного соединения проводников 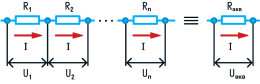 При последовательном соединении сила тока в любых частях цепи одна и та же: I = I1 = I2 = … = In. Если в цепи с последовательным способом соединения одна из ламп выйдет из строя и через нее не будет протекать электрический ток, то и через оставшиеся лампы ток проходить не будет. Вспомним Анфису и ее гирлянду: когда одна из зеленых лампочек перегорела, то ток, проходящий через нее, стал равен нулю. Следовательно, и другие зеленые лампочки, включенные последовательно, не загорелись. Чтобы починить гирлянду, нужно определить перегоревшую лампочку и заменить ее. При последовательном соединении общее сопротивление цепи равно сумме сопротивлений отдельных проводников: Rэкв = R1 + R2 + … + Rn. При последовательном соединении общее напряжение цепи равно сумме напряжений на отдельных участках: Uэкв = U1 + U2 + … + Un. Параллельное соединение проводников При параллельном соединении начала всех проводников соединяются в одной общей точке электрической цепи, а их концы — в другой. 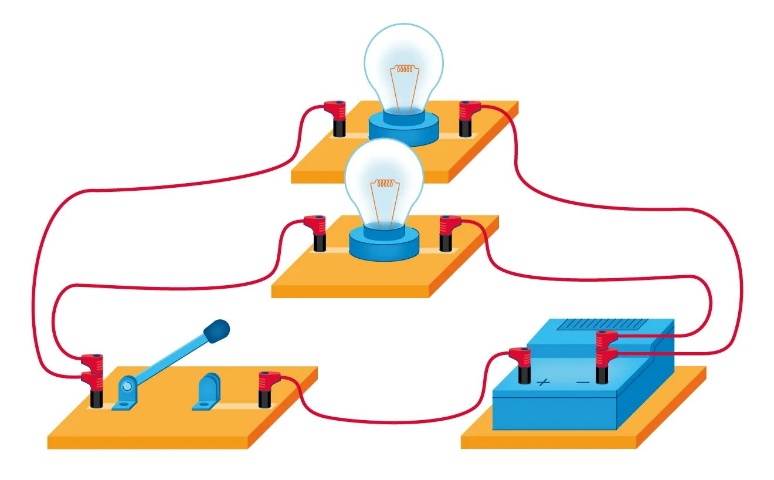 Параллельное соединение используют в тех случаях, когда необходимо подключать электроприборы независимо друг от друга. Например, если отключить чайник, то холодильник будет продолжать работать. А когда в люстре перегорает одна лампочка, остальные все так же освещают комнату. Приведем еще несколько примеров применения параллельного способа соединения: освещение в больших торговых залах; бытовые электроприборы в квартире; компьютеры в кабинете информатики; вольтметр для измерения напряжения на участке цепи. Параллельное соединение проводников: формулы 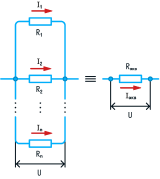 Напряжение при параллельном соединении в любых частях цепи одинаково: U = U1 = U2 = … = Un. Как вы помните, все бытовые электроприборы рассчитаны на одинаковое номинальное напряжение 220 В. Да и согласитесь, куда проще делать все розетки одинаковыми, а не рассчитывать напряжение для каждого прибора при их последовательном соединении. Сила тока при параллельном соединении (в неразветвленной части цепи) равна сумме сил тока в отдельных параллельно соединенных проводниках: Iэкв = I1 + I2 + … + In. Электрический ток растекается по ветвям обратно пропорционально их сопротивлениям. Если сопротивления в ветвях равны, то и ток при параллельном соединении делится между ними поровну. Общее сопротивление цепи определяется по формуле: 1 / Rэкв = 1 / R1 + 1 / R2 + … + 1 / Rn Для двух параллельно соединенных проводников формулу можно записать иначе: Rэкв = (R1 · R2) / (R1 + R2). Если n одинаковых проводников, каждый из которых имеет сопротивление R1, соединены параллельно, то общее сопротивление участка цепи можно найти, разделив сопротивление одного из проводников на их количество: Rэкв = R1 / n. 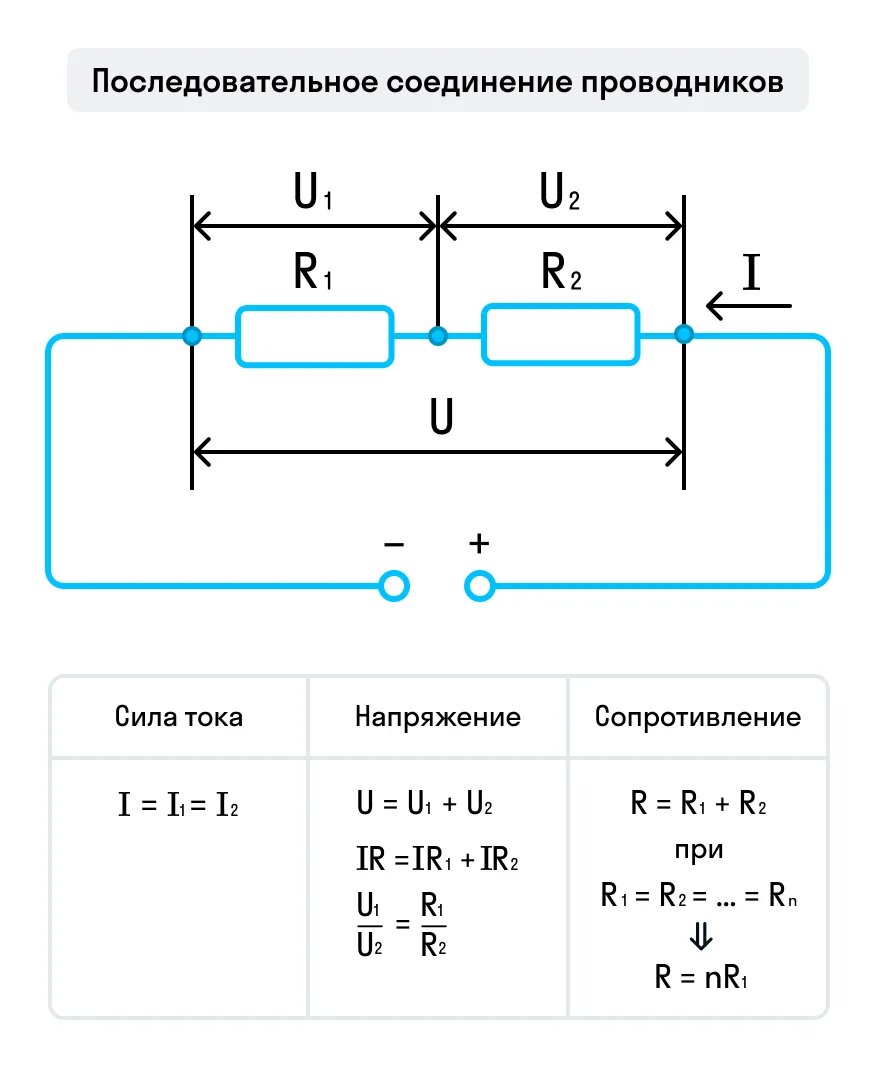  22. Разветвленные цепи. Правила Кирхгофа Расчет разветвленных цепей, например нахождение токов в отдельных ее ветвях, значительно упрощается, если пользоваться двумя правилами Кирхгофа. Чтобы расчеты сложных электрических цепей с неоднородными участками не вызывали трудности, существует упрощение с помощью применения правил Кирхгофа, которые рассматривают как обобщение закона Ома на случай разветвленных цепей. В таких цепях выделяют узловые точки, называемые узлами, где сходятся не менее трех проводников, как изображено на рисунке. Токи, поступающие в узел, считают положительными, а вытекающие – отрицательными. 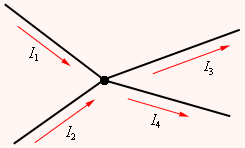 Узел электрической цепи. I1, I2>0; I3, I4<0 Узел электрической цепи. I1, I2>0; I3, I4<0Правила Кирхгофа. Примеры Определение 1 В узлах цепи с постоянным током не происходит накопление зарядов. Получаем первое правило (закон) Кирхгофа: Алгебраическая сумма сил токов для каждого узла разветвленной цепи равняется нулю: I1+I2+I3+...+In=0 Данное правило принято считать следствием закона сохранения электрического заряда. Определение 2 Наличие разветвленной цепи позволяет выделить несколько замкнутых путей, которые состоят из однородных и неоднородных участков. Их принято называть контурами. На участках с выделенным контуром могут протекать различные токи. Рисунок наглядно показывает пример такой цепи, соответствующей 1 закону Кирхгофа. Она состоит из двух узлов a и d, в которых сходятся одинаковые токи. Только один из заданных узлов будет независимым. 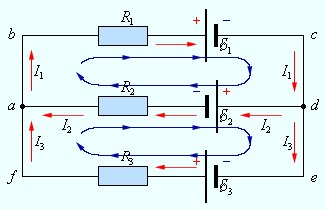 Пример разветвленной электрической цепи. Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef). Рис.1.10.2 Пример разветвленной электрической цепи. Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef). Рис.1.10.2В предложенной цепи выделяют три контура вида abcd, adef и abcde f. Независимыми считаются только два: abcd и adef. Последний из вышеперечисленных не имеет никаких новых участков. Второе правило Кирхгофа – это следствие обобщенного закона Ома. Для записи обобщенного закона Ома участков, составляющих один из контуров цепи, используется пример, изображенный на рисунке выше для abcd. Каждому участку задаются положительные направления тока и обхода контура. Для записи следует учитывать «правила знаков», приведенные на рисунке. 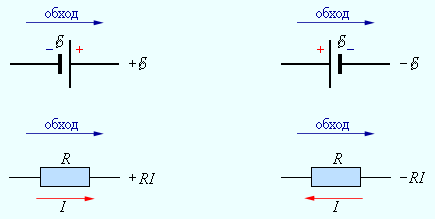 «Правила знаков».рис 1.10.3 «Правила знаков».рис 1.10.3Запись обобщенного закона Ома для участков контура abcd принимает вид  Определение 3 Формулировка 2 правила или закона Кирхгофа: алгебраическая сумма сопротивления каждого из участков любого замкнутого контура разветвленной цепи постоянного тока на силу тока этого участка равняется сумме ЭДС вдоль этого контура. Модель постоянного тока Оба правила Кирхгофа для всех узлов и контуров разветвленной цепи дают необходимое и достаточное число алгебраических уравнений для расчета значений напряжений и сил токов электрической цепи. Цепь, изображенная на рисунке 1.10.2, рассматривается как система уравнений для определения трех неизвестных 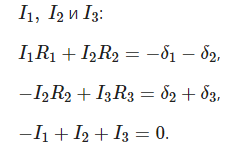 То есть применение этих правил помогает свести расчет электрической цепи постоянного тока к решению системы. Процесс не вызывает трудностей, но зачастую приходится работать с громоздкими выражениями простых цепей. При получении отрицательного значения силы тока на участке цепи говорят о противоположном направлении тока, относительно выбранного.   Модель цепи постоянного тока. Модель конденсаторов в цепях постоянного тока. 26. Явление Зеебека и Пельтье. Известно, что работа выхода электронов из металла зависит от температуры. Следовательно, контактная разность потенциалов также зависит от температуры. Если температура контактов замкнутой цепи, состоящей из нескольких металлов, неодинакова, то полная э. д. с. контура не будет равна нулю, и в цепи возникает электрических ток. Явление возникновения термоэлектрического тока (эффект Зеебека) и связанные с ним эффекты Пельтье и Томсона относятся к термоэлектрическим явлениям. |

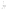 , а
, а 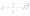 , тогда как опыт показывает, что
, тогда как опыт показывает, что