Коллоквиум Физика. Коллоквиум. 17. Природа носителей заряда. Классическая теория электропроводности металлов Формула Друде

• Название: 17. Природа носителей заряда. Классическая теория электропроводности металлов Формула Друде
• Анкор: Коллоквиум Физика
• Дата: 01.12.2022
• Размер: 3.24 Mb.
• Имя файла: Коллоквиум.docx
• Тип: Закон; #822924
• страница: 9 из 14

 Вывод основного закона электромагнитной индукции из закона сохранения и превращения энергии

Основной закон электромагнитной индукции (закон Фарадея) можно вывести из закона сохранения и превращения энергии, что и было сделано Гельмгольцем (1847 г.).

Пусть имеется замкнутая цепь (контур с током), содержащая источник ЭДС, величина которой , и пусть полное сопротивление этой цепи равно R. Обозначим силу тока в цепи через I. Количество энергии, затрачиваемое источником ЭДС за время dt, как известно, равно

.

Если внешнее магнитное поле отсутствует или контур неподвижен, то вся эта энергия превращается в тепло, количество которого определяется законом Джоуля-Ленца:

.

Имеем

.

Откуда после сокращения на dt получим закон Ома для замкнутой (полной) цепи в интегральной форме:

и  . (4.11)

При перемещении такого контура с источником ЭДС (с током) в магнитном поле часть энергии источника тока будет расходоваться против перемещения контура в магнитном поле, а часть выделяться в контуре в виде тепла. Расходование энергии источника тока против перемещения контура с током в магнитном поле связано с тем, что для получения индукционных токов методом перемещения проводника в магнитном поле необходимо совершить работу, так как сила, действующая на индукционный ток, препятствует перемещению проводника.

Известно, что работа по перемещению проводника с током в магнитном поле dA = IdФ, где dФ – величина изменения магнитного потока, сцепленного с данным контуром.

Так как при таком перемещении магнитное поле остается неизменным, то эта работа может совершаться лишь за счет энергии источника тока.

На основании закона сохранения и превращения энергии будем иметь



или

.

Откуда

. (4.12)

Решая уравнение (4.12) относительно силы тока, найдем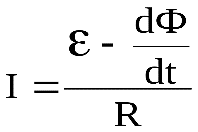

. (4.13)

Принимая равенство (4.13) за математическое выражение закона Ома и сравнивая его с полученным ранее для этого же контура в отсутствие магнитного поля, можно установить, что благодаря изменению потока магнитной индукции к имевшейся в цепи ЭДС источника прибавилась ЭДС:

. (4.14)

Как видно, величина ЭДС электромагнитной индукции не зависит от величины  источника тока и, значит, сохранит свое значение и при  = 0, т.е. будет возникать вне зависимости от всяких других ЭДС, действующих в той же цепи.

Знак «минус» служит математическим выражением правила (закона) Ленца.

Таким образом, формула (4.14) является математическим выражением основного закона электромагнитной индукции (в формулировке Максвелла).

Аналогично можно получить вывод этого закона и для отрезка проводника (в формулировке Фарадея).

43. Закон Фарадея. Вывод из закона сохранения энергии. Правило Ленца.

Закон Фарадея и его вывод из закона сохранения энергии

Обобщая результаты своих многочислен­ных опытов, Фарадей пришел к количе­ственному закону электромагнитной ин­дукции. Он показал, что всякий раз, когда происходит изменение сцепленного с кон­туром потока магнитной индукции, в кон-

194

туре возникает индукционный ток; возник­новение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой элек­тромагнитной индукции. Значение индук­ционного тока, а следовательно, и э. д. с, электромагнитной индукции ξ_iопределя­ются только скоростью изменения магнит­ного потока, т. е.



Теперь необходимо выяснить знак ξ_i. В § 120 было показано, что знак магнитно­го потока зависит от выбора положитель­ной нормали к контуру. В свою очередь, положительное направление нормали свя­зано с током правилом правого винта (см. § 109). Следовательно, выбирая опре­деленное положительное направление нор­мали, мы определяем как знак потока маг­нитной индукции, так и направление тока и э.д.с. в контуре. Пользуясь этими пред­ставлениями и выводами, можно соответ­ственно прийти к формулировке закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватыва­емого замкнутым проводящим контуром, возникающая в контуре э.д.с.



Знак минус показывает, что увеличе­ние потока (dФ/dt>0) вызывает э.д.с.

ξξ_i<0, т. е. поле индукционного тока на­правлено навстречу потоку; уменьшение

потока (dФ/dt<0 ) вызывает ξ_i>0,

т. е. направления потока и поля индукци­онного тока совпадают. Знак минус в фор­муле (123.2) является математическим выражением правила Ленца — общего правила для нахождения направления ин­дукционного тока, выведенного в 1833 г.

Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного по­тока, вызвавшего этот индукционный ток.

Закон Фарадея (см. (123.2)) может быть непосредственно получен из закона сохранения энергии, как это впервые сде­лал Г. Гельмгольц. Рассмотрим проводник с током I, который помещен в однородное магнитное поле, перпендикулярное плоско­сти контура, и может свободно переме­щаться (см. рис. 177). Под действием си­лы Ампера F, направление которой пока­зано на рисунке, проводник перемещается на отрезок dx. Таким образом, сила Ампе­ра производит работу (см.(121.1)) dA=IdФ, где dФ — пересеченный проводни­ком магнитный поток.

Если полное сопротивление контура равно R, то, согласно закону сохранения энергии, работа источника тока за вре­мя dt (ξIdt) будет складываться из рабо­ты на джоулеву теплоту (I²Rdt) и работы по перемещению проводника в магнитном поле (IdФ):



откуда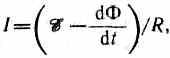



где-dФ/dt=ξ_iесть не что иное, как закон Фарадея (см. (123.2)).

Закон Фарадея можно сформулиро­вать еще таким образом: э.д.с. ξ_i элек­тромагнитной индукции в контуре числен­но равна и противоположна по знаку ско­рости изменения магнитного потока сквозь поверхность, ограниченную этим конту­ром. Этот закон является универсальным: э.д.с. ξ_iне зависит от способа изменения магнитного потока.

Э.д.с. электромагнитной индукции выражается в вольтах. Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим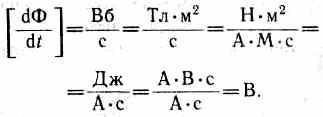



Какова природа э.д.с. электромагнит­ной индукции? Если проводник (подвиж­ная перемычка контура на рис. 177) дви-

195

жется в постоянном магнитном поле, то сила Лоренца, действующая на заряды внутри проводника, движущиеся вместе с проводником, будет направлена противо­положно току, т. е. она будет создавать в проводнике индукционный ток противо­положного направления (за направление электрического тока принимается движе­ние положительных зарядов). Таким обра­зом, возбуждение э.д.с. индукции при движении контура в постоянном магнит­ном поле объясняется действием силы Ло­ренца, возникающей при движении про­водника.

Согласно закону Фарадея, возникнове­ние э.д.с. электромагнитной индукции возможно и в случае неподвижного кон­тура, находящегося в переменном магнит­ном поле. Однако сила Лоренца на непод­вижные заряды не действует, поэтому в данном случае ею нельзя объяснить воз­никновение э.д.с. индукции. Максвелл для объяснения э.д.с. индукции в непод­вижных проводниках предположил, что всякое переменное магнитное поле воз­буждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в проводнике. Циркуляция векто­ра Е_Вэтого поля по любому неподвижному контуру L проводника представляет собой э.д.с. электромагнитной индукции: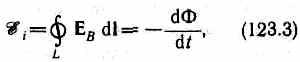



44. Природа э.д.с. электромагнитной индукции: в движущемся проводнике и в случае движения магнитного поля относительно неподвижного проводника.