Коллоквиум Физика. Коллоквиум. 17. Природа носителей заряда. Классическая теория электропроводности металлов Формула Друде

• Название: 17. Природа носителей заряда. Классическая теория электропроводности металлов Формула Друде
• Анкор: Коллоквиум Физика
• Дата: 01.12.2022
• Размер: 3.24 Mb.
• Имя файла: Коллоквиум.docx
• Тип: Закон; #822924
• страница: 12 из 14

Намагниченность. Магнитное поле в веществе

Подобно тому, как для количественного описания поляризации диэлектриков вводи­лась

поляризованность (см. § 88), для количественного описания намагничения магнетиков

вводят векторную величину — намагниченность, определяемую магнитным моментом

единицы объема магнетика:  где — магнитный момент

магнетика, представляющий собой векторную сумму магнитных моментов отдельных

молекул

• 
  вектор магнитной индукции В, характеризующий результирующее магнитное поле, создава­емое всеми макро- и микротоками, ивектор напряженности Н, характеризующий магнитное поле макротоков. Следовательно, магнитное поле в веществе складывается из двух полей: внешнего поля, создаваемого током, и поля, создаваемого намагничен­ным веществом. Тогда можем записать, что вектор магнитной индукции результирующего магнитного ноля в магнетике равен векторной сумме магнитных индукций внешнего поляВ₀(поля, создаваемого намагничивающим током в вакууме) и поля микротоковВ' (поля, создаваемого молекулярными токами): (133.1) гдеВ₀=₀Н
  
• 
  Как показывает опыт, в несильных полях намагниченность прямо пропорциональ­на напряженности поля, вызывающего намагничение, т. е. (133.6)
  

где — безразмерная величина, называемая магнитной восприимчивостью вещества. Для диамагнстиховотрицательна (поле молекулярных токов противоположно вне­шнему), для парамагнетиков — положительна (поле молекулярных токов совпадает с внешним).

Используя формулу (133.6), выражение (133.4) можно записать в виде (133.7) откуда Безразмерная величина (133.8)

представляет собой магнитную проницаемость вещества. Подставив (133.8) в (133.7), придем к соотношению (109.3) В=₀Н, которое ранее постулировалось.

Так как абсолютное значение магнитной восприимчивости для диа- и парамагнетиковочень мало (порядка 10^–4—10^–6), то для нихнезначительно отличается от единицы. Это просто понять, так как магнитное поле молекулярных токов значительно слабее намагничивающего поля. Таким образом, для диамагнетиков<0 и<1, для парамагнетиков>0 и>1.

• 
  Величина, характеризующая способность вещества намагничиваться, называется магнитная проницаемость (µ).Она показывает, во сколько раз магнитная индукция в данном веществе больше или меньше магнитной индукции в вакууме.
  

Магнитная индукция в какой-либо точке поля в данной среде определяется по формуле 

где B – магнитная индукция в теслах;

I – величина тока в амперах;

L – расстояние от оси провода до исследуемой точки поля в метрах;

µ — магнитная проницаемость среды.

За единицу измерения магнитной проницаемости в Международной системе единиц принят 1 генри на метр.

Магнитная проницаемость среды равна 1 гн/м, если в точке, удаленной от оси проводника с током на 1 метр, при силе тока, равной 2π ампера, магнитная индукция равна 1 тесле.

Величина магнитной проницаемости среды может быть выражена в виде произведения двух сомножителей

где µ — магнитная проницаемость среды;

µ0 – магнитная проницаемость вакуума;

µr – относительная магнитная проницаем ость, представляющая собой отвлеченное число, показывающее отношение величины магнитной проницаемости данного вещества к магнитной проницаемости вакуума.

Магнитная проницаемость вакуума µ0 в Международной системе единиц равна

• 
  Вектор намагничивания— магнитный момент элементарного объёма, используемый для описания магнитного состояния вещества. По отношению к направлению вектора магнитного поля различают продольную намагниченность и поперечную намагниченность. Поперечная намагниченность достигает значительных величин в анизотропных магнетиках, и близка к нулю в изотропных магнетиках. Поэтому, в последних возможно выразить вектор намагничивания через напряжённость магнитного поля и коэффициент названный магнитной восприимчивостью: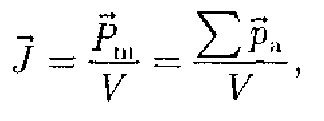
  

• 
  Закон полного тока для магнитного поля в веществе (теорема о циркуляции вектора В) является обобщением закона (118.1):
  

где IиI'— соответственно алгебраические суммы макротоков (токов проводимости) и микротоков (молекулярных токов), охватываемых произвольным замкнутым кон­туромL.Таким образом, циркуляция вектора магнитной индукцииВпо произволь­ному замкнутому контуру равна алгебраической сумме токов проводимости и молеку­лярных токов, охватываемых этим контуром, умноженной на магнитную постоянную. ВекторВ, таким образом, характеризует результирующее поле, созданное как мак­роскопическими токами в проводниках (токами проводимости), так и микроскопичес­кими токами в магнетиках, поэтому линии вектора магнитной индукцииВне имеют источников и являются замкнутыми.

Из теории известно, что циркуляция намагниченности Jпо произвольному замкну­тому контуруLравна алгебраической суммемолекулярных токов,охватываемых этим контуром:

Тогда закон полного тока для магнитного поля в веществе можно записать также в виде (133.9)

где I,подчеркнем этоещераз, есть алгебраическая сумма токов проводимости.

Выражение, стоящее в скобках в (133.9), согласно (133.5), есть не что иное, как введенный ранее вектор Hнапряженности магнитного поля. Итак, циркуляция вектораНпо произвольному замкнутому контуруLравна алгебраической сумме токов проводимости, охватываемых этим контуром: (133.10)

Выражение (133.10) представляет собой теорему о циркуляции вектора Н.

Циркуляция вектора напряженности магнитного поля в веществе: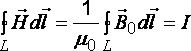

• 
  Напряженность магнитного поля[H] – это отношение магнитной индукции к магнитной проницаемости среды
  

Напряженность магнитного поля в СИ - ампер на метр (А/м).

Векторы индукции (В) и напряженности магнитного поля (Н) совпадают по направлению. Если знать Напряженность магнитного поля в данной точке, то можно определить индукцию поля в этой точке.

Напряженность магнитного поля зависит только от силы тока, протекающего по проводнику, и его геометрии.