Коллоквиум Физика. Коллоквиум. 17. Природа носителей заряда. Классическая теория электропроводности металлов Формула Друде

• Название: 17. Природа носителей заряда. Классическая теория электропроводности металлов Формула Друде
• Анкор: Коллоквиум Физика
• Дата: 01.12.2022
• Размер: 3.24 Mb.
• Имя файла: Коллоквиум.docx
• Тип: Закон; #822924
• страница: 11 из 14

47. Взаимная индукция.

Если проводящие контура или проводники расположены достаточно близко, то при изменении силы тока в одном из них через поверхность, ограниченную вторым изменяется магнитный поток, и, соответственно, в нем возникает индукционный ток. Такие контура называются «сцепленными» или индуктивно связанными (рис.115).

Магнитное поле первого тока создает поток через поверхность второго контура   и наоборот   .

L₂₁ и L₁₂ - называются коэффициентами взаимной индукции, зависят от геометрической формы, размеров, взаимного расположения контуров и магнитных характеристик среды.

Расчеты и эксперименты показывают, что при неизменной величине перечисленных параметров коэффициенты взаимной индукции равны L₂₁=L₁₂.

Это свойство коэффициентов взаимной индукции позволяет значительно упростить расчет самих коэффициентов, а также магнитных потоков, и, поэтому это равенство принято называть теоремой взаимности.

На практике взаимная индукция проявляется при прохождении тока по коаксиальному кабелю (рис.116), по двухпроводной линии (рис.117) и т.п.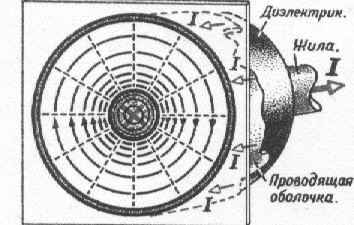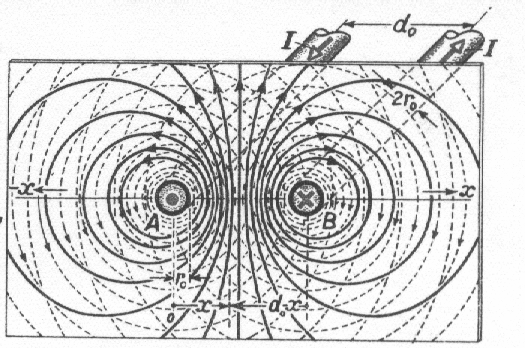

 

РИС.118 РИС.119

Явление взаимной индукции двух катушек (рис.120), намотанных на общий сердечник, лежит в основе трансформаторов, широко используемых устройств для повышения или понижения напряжения переменного тока. На рис. 121 приведен внешний вид демонстрационного трансформатора, принципиальное устройство и принятое обозначение трансформатора в электрической схеме.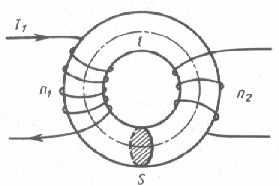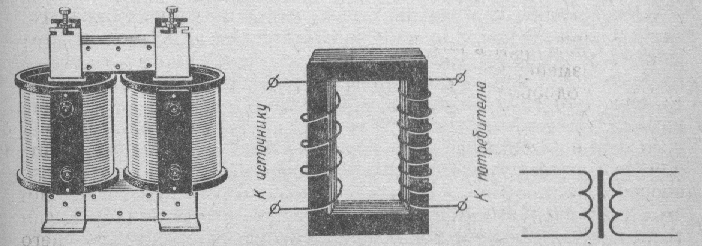

 

Рис.120 РИС.121

48. Энергия магнитного поля. Энергия магнитного поля соленоида.

Проводник, c протекающим по нему электрическим ток, всегда окружен магнитным полем, причем магнитное поле исчезает и появляется вместе с исчезновением и появлением тока. Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля.

Рассмотрим контур индуктивностью L, по которому протекает ток I. С этим контуром сцеплен магнитный поток Ф=LI, поскольку индуктивность контура неизменна, то при изменении тока на dI магнитный поток изменяется на dФ=LdI. Но для изменения магнитного потока на величину dФ следует совершить работу dА=IdФ=LIdI. Тогда работа по созданию магнитного потока Ф равна



Значит, энергия магнитного поля, которое связано с контуром,

 (1)

Энергию магнитного поля можно рассматривать как функцию величин, которые характеризуют это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (1) формулу индуктивности соленоида, найдем



Так как I=Bl/(μ0μN) и В=μ0μH , то

 (2)

где Sl = V — объем соленоида.

Магнитное поле внутри соленоида однородно и сосредоточено внутри него, поэтому энергия (2) заключена в объеме соленоида и имеет с нем однородное распределение с постоянной объемной плотностью

 (3)

Формула (3) для объемной плотности энергии магнитного поля имеет вид, аналогичный выражению для объемной плотности энергии электростатического поля, с тем отличием, что электрические величины заменены в нем магнитными. Формула (3) выводилась для однородного поля, но она верна и для неоднородных полей. Формула (3) справедлива только для сред, для которых линейная зависимость В от Н , т.е. оно относится только к пара- и диамагнетикам.

Плотность энергии магнитного поля в соленоиде с сердечником будет складываться из энергии поля в вакууме и в магнетике сердечника: 

, отсюда 

Т.к. в вакууме   , имеем 

49. Токи при размыкании и замыкании цепи.

При всяком изменении силы тока в проводящем контуре возникает э.д.с. самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Экстратоки самоиндукции, согласно правилу Ленца, всегда направлены так, чтобы препятствовать изменениям тока в цепи, т.е. направлены противоположно току, создаваемому источником. При выключении источника тока экстратоки имеют такое же направление, что и ослабевающий ток. Следовательно, наличие индуктивности в цепи приводит к замедлению исчезновения или установления тока в цепи.

Рассмотрим процесс выключения тока в цепи, содержащей источник тока с э.д.с. E_i, сопротивление R и индуктивность L. Под действием внешней э.д.с. в цепи течет постоянный ток I_o =E/R (внутренним сопротивлением источника тока пренебрегаем).

В момент времени t = 0 отключим источник тока. Ток через катушку индуктивности начнет уменьшаться, что приведет к возникновению эдс самоиндукции E_s= –L(dI/dt), препятствующей, согласно правилу Ленца, уменьшению тока. В каждый момент времени ток в цепи определяется законом Ома I =E_s/R, или

IR =–L(dI/dt). (18.1)

Разделив переменные, получим dI/I = – Rdt/L. Интегрируя это уравнение по I (от I_o до I) и t (от 0 до t), находим ln(I/I_o) = – Rt/L, или

I(t) =I_o exp (– t/τ), (18.2)

где τ =L/R – постоянная, называемая временем релаксации, равная времени, в течение которого сила тока уменьшается в е раз.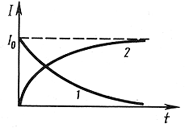

 Таким образом, в процессе отключения источника э.д.с. сила тока убывает по экспоненциальному закону (18.2) и определяется кривой 1 на рис. (19). Чем больше индуктивность цепи и меньше сопротивление, тем больше τ и, следовательно, тем медленнее уменьшается ток в цепи при ее размыкании.

При замыкании цепи помимо внешней э.д.с E возникает э.д.с самоиндукции E_s= –L(dI/dt), препятствующая, согласно правилу Ленца, возрастанию тока. По закону Ома IR = E + E_s или

IR = E –L(dI/dt). Введя новую переменную u = IR – E, преобразу- Рис.19. ем это уравнение к виду du/u = – dt/τ , где τ – время релаксации.

В момент замыкания (t = 0) сила тока I =0 и u = –E. Следовательно, интегрируя по u (от –E до IR–E) и t (от 0 до t), находим ln[(IR–E)/(–E)] = –t/τ, или

I(t)=I_o[1-exp(–t/τ)], (18.3)

где I_o= E/R – установившийся ток (при t → ¥).

Таким образом, в процессе включения источника э.д.с нарастание силы тока в цепи задается функцией (18.3) и определяется кривой 2 на рис.19. Сила тока возрастает от начального значения I=0 и асимптотически стремится к установившемуся значению I_o= E/R. Скорость нарастания тока определяется тем же временем релаксации τ =L/R, что и убывание тока. Установление тока происходит тем быстрее, чем меньше индуктивность цепи и больше ее сопротивление.

Контур, содержащий индуктивность, нельзя резко размыкать, так как возникновение при этом значительных э.д.с. самоиндукции может привести к пробою изоляции и выводу из строя электрических приборов.

Трансформаторы.

Принцип действия трансформаторов, применяемых для повышения или понижения напряжения переменного тока, основан на явлении взаимной индукции. Первые трансформаторы были сконструированы и введены в практику русским электротехником П.Н.Яблочковым (1847 – 1894) и русским физиком И.Ф.Усагиным (1855 – 1919). Принципиальная схема трансформатора показана на рис. 20.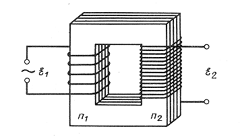

 Первичная и вторичная катушки (обмотки), имеющие соответственно n₁ и n₂ витков, укреплены на замкнутом железном сердечнике. Так как концы первичной обмотки присоединены к источнику переменного напряжения с э.д.с. E₁, то в ней возникает переменный ток создающий в сердечнике трансформатора переменный магнитный поток Ф, который практически полностью локализован в

железном сердечнике и, следовательно, почти целиком

Рис.20.

пронизывает витки вторичной обмотки. Изменение этого потока вызывает во вторичной обмотке появление э.д.с. электромагнитной индукции, а в первичной – э.д.с. самоиндукции.

По закону Ома, ток I₁, первичной обмотки определяется алгебраической суммой внешней э.д.с. и э.д.с. самоиндукции: I₁R₁=[E_i–d(n₁Ф)/dt], где R₁ – сопротивление первичной обмотки. Падение напряжения I₁R₁ на сопротивлении R₁, при быстропеременных полях мало по сравнению с каждой из двух э.д.с., поэтому E₁»n₁dФ/dt.

Э.д.с. электромагнитной индукции, возникающая во вторичной обмотке,

E₂= –[(dn₂Ф)/dt] = – n₂(dФ/dt). (19.1)

Сравнивая выражения для E₁ и E₂, получим, что э.д.с., возникающая во вторичной обмотке,

E₂= –(n₂/n₁) E₁, (19.2)

где знак минус показывает, что э.д.с. в первичной и вторичной обмотках противоположны по фазе. Отношение числа витков n₁/n₂ показывающее, во сколько раз э.д.с. во вторичной обмотке трансформатора больше (или меньше), чем в первичной, называется коэффициентом трансформации.

Пренебрегая потерями энергии, которые в современных трансформаторах не превышают 2% и связаны в основном с выделением в обмотках джоулевой теплоты и появлением вихревых токов, и применяя закон сохранения энергии, можем записать, что мощности тока в обеих обмотках трансформатора практически одинаковы:

E₂ I₂ ≈ E₁I₁, (19.3)

откуда, учитывая соотношение (19.2), найдем E₂ /E₁ = I₁/I₂ = n₂/n₁, т.е. токи в обмотках трансформатора обратно пропорциональны числу витков в этих обмотках.

Если n₂/n₁>1, то имеем дело с повышающим трансформатором, увеличивающим переменную э.д.с. и понижающим ток (применяется, например, для передачи электроэнергии на большие расстояния, так как в данном случае потери на джоулеву теплоту, пропорциональные квадрату силы тока, снижаются). Если n₂/n₁<1, то имеем дело с понижающим трансформатором, уменьшающим э.д.с. и повышающим ток (применяется, например, при электросварке, так как для нее требуется большой ток при низком напряжении).

Трансформаторы, используемые в радиотехнике, имеют 4–5 обмоток, обладающих разными рабочими напряжениями. Трансформатор, состоящий из одной обмотки, называется автотрансформатором. В случае повышающего автотрансформатора э.д.с. подводится к части обмотки, а вторичная э.д.с. снимается со всей обмотки. В понижающем автотрансформаторе напряжение сети подается на всю обмотку, а вторичная э.д.с. снимается с части обмотки.

52. Природа парамагнетизма. Закон Кюри-Вейсса.

В отличие от диамагнетиков, в парамагнетиках намагниченность направлена по полю, т. е.  >0. Парамагнитная восприимчивостьзависит от температуры:



Эта зависимость впервые была установлена П. Кюри и носит на­звание закона Кюри. Величина С - постояннаяй Кюри.

Парамагнетизмом обладают:

- атомы и молекулы, имеющие нечетное число электронов (например, свободные атомы щелочных элементов, молекула оки­си азота NO, некоторые свободные органические радикалы). У этих атомов и молекул имеется нескомпенсированный спиновый маг­нитный момент;

- свободные атомы и ионы, имеющие недостроенные внутрен­ние оболочки (например, переходные элементы Fe, Co, Ni и т. д., а также редкоземельные элементы). В этом случае с каждым атомом или ионом связан магнитный момент, обусловленный нескомпенсированностью спинов одного или нескольких электронов не­достроенной d- или f-оболочки. В ряде случаев парамагнетизм обнаруживается и в твердых телах, состоящих из указанных атомов;

- некоторые молекулы с четным числом электронов (напри­мер,  иS₂). В них тоже имеется магнитный момент, связанный с нескомпенсированностью спинов двух электронов;

- дефекты кристаллической решетки с нечетным числом электронов.

- металлы.

Вп 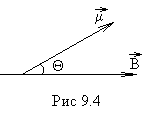ервые теория парамагнитной восприимчивости была создана П. Ланжевеном. Следуя Ланжевену, рассмотрим среду, со­держащую N атомов в единичном объеме. Пусть каждый атом име­ет постоянный магнитный момент  и взаимодействие между маг­нитными моментами атомов отсутствует . В отсутствие магнитного поля эти моменты ориентированы случайным образом, так что ре­зультирующая намагниченность равна нулю. При наложении маг­нитного поля эти моменты ориентируются в направлении поля. В результате этого появляется направленная по полю намагничен­ность. Ориентирующему действию поля препятствует тепловое движение.

. Энергия «магнитного диполя»   в магнит­ном поле с индукцией 



где  —угол между векторами и   (рис.9. 4). Она минималь­на при  .

Магнитный момент вещества складывается из проекций магнит­ных моментов отдельных атомов на направление поля. Среднее значение проекции магнитного момента: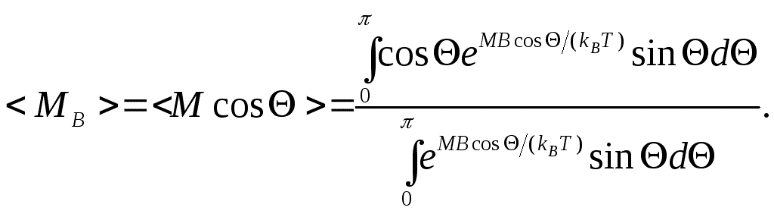



Вычисление среднего приводит к известному результату:

,

где L( ) — функция Ланжевена,  .Результирующая намагниченность

J=N=NML( ).

При  < . Таким образом, и парамагнитная восприимчивость



Видим, что k_mобратно пропорциональна температуре, что полно­стью согласуется с опытом (закон Кюри). Постоянная Кюри С=

Проекции магнитного момента атома на направление магнитного поля 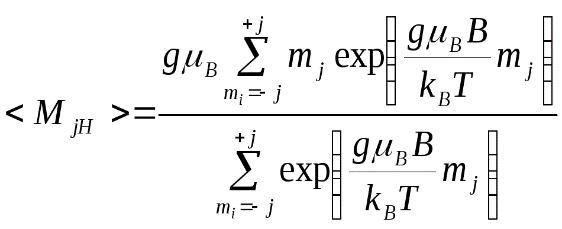 .Здесь маг­нитное квантовое число  может иметь 2j+1 значение: j, j-1, . . ., -j. С учетом этого среднее значение проекции магнитного мо­мента на направление поля запишем в виде

.

Вычислив сумму, получим следующее выражение:

,

где обозначено  , Функция - обобщенная функция Ланжевена, называемая также функцией Бриллюэна. Тогда намагниченность

.

При  это выражение переходит в классическую формулу Ланжевена .

Если магнитный момент атома обусловлен только спином электрона (орбитального момента нет), то число возможных ориентации момента в магнитном поле уменьшается до двух (L=0; j = S = ±1/2). При этом намагниченность принимает более простой вид



В случае слабых полей и не очень низких температур ( <
.

Это закон Кюри, постоянная Кюри  и только заменено на  .

В сильных полях и при очень низких температурах намагниченность достигает насыщения:



Парамагнетизм обнаруживают атомы, имеющие неспаренные спины или нескомпенсированный момент импульса, т. е. атомы с нечетным числом электронов или с частично заполненной внутрен­ней оболочкой. Характер заполнения электронных оболочек опре­деляется правилами Хунда. Согласно этим правилам, спины элек­тронов в оболочке всегда складываются друг с другом так, что­бы дать максимально возможные значении момента импульса и магнитного момента.

Закон Кюри — Вейса — описывает магнитную восприимчивость ферромагнетика в области температур выше точки Кюри.




При T = Tc магнитная восприимчивость стремится к бесконечности. При снижении температуры до точки Кюри и ниже возникает спонтанная намагниченность вещества.

Закон Кюри — Вейса выполняется также для антиферромагнетиков при температурах выше точки Нееля. В этом случае константа Tc в формуле отрицательна, её абсолютное значение по порядку величины близко к температуре Нееля.

Тут мы использовали :

 — Магнитная восприимчивость

 — Постоянная Кюри, зависящая от данного вещества

 — Абсолютная температура в кельвинах

 — Температура Кюри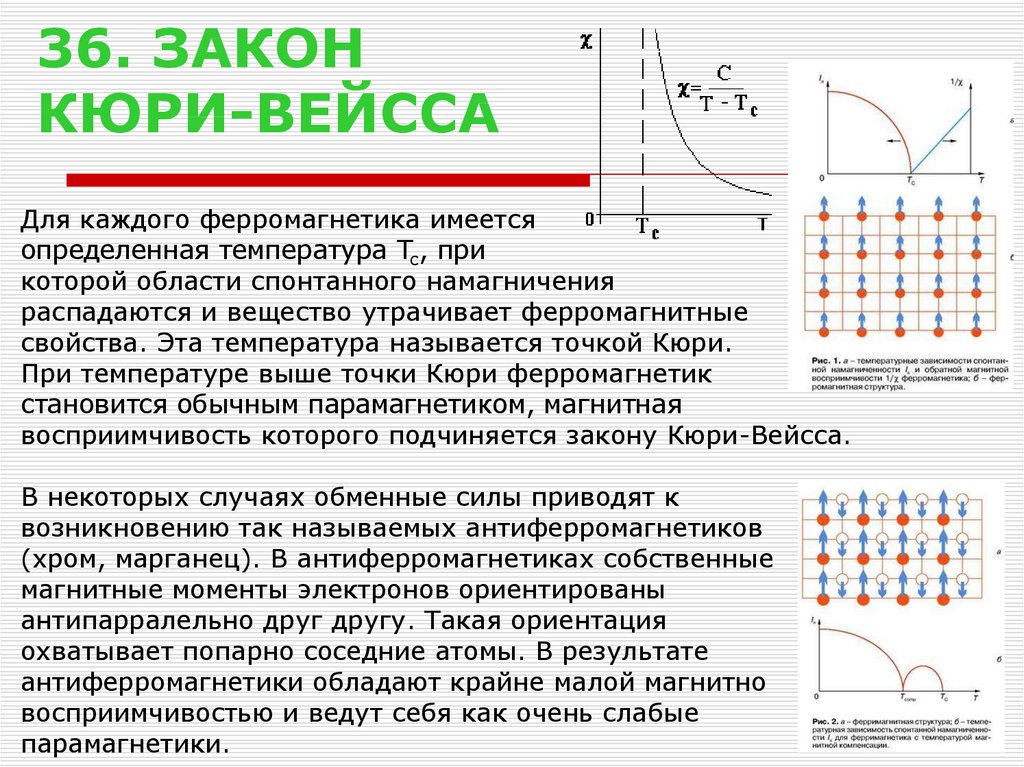



52. Намагниченность. Магнитное поле в веществе. Магнитная проницаемость и восприимчивость