Коллоквиум Физика. Коллоквиум. 17. Природа носителей заряда. Классическая теория электропроводности металлов Формула Друде

• Название: 17. Природа носителей заряда. Классическая теория электропроводности металлов Формула Друде
• Анкор: Коллоквиум Физика
• Дата: 01.12.2022
• Размер: 3.24 Mb.
• Имя файла: Коллоквиум.docx
• Тип: Закон; #822924
• страница: 8 из 14

Физика ускорителей

Как са­мо­сто­ят. дис­ци­п­ли­на воз­ник­ла в пер­вые де­ся­ти­ле­тия 20 в., вы­де­лив­шись из бо­лее ши­ро­ко­го кру­га дис­ци­п­лин (фи­зи­ка плаз­мы и пуч­ков за­ря­жен­ных час­тиц, тех­ни­ка элек­тро­ва­ку­ум­ных при­бо­ров и др.), свя­зан­ных с ис­сле­до­ва­ни­ем про­те­ка­ния элек­трич. то­ка в раз­ре­жен­ных га­зах. В этом раз­де­ле при­клад­ной фи­зи­ки изу­ча­ют­ся: ди­на­ми­ка час­тиц в У. з. ч., а так­же мно­го­числ. тех­нич. за­да­чи, свя­зан­ные с со­ору­же­ни­ем и экс­плуа­та­ци­ей ус­ко­ри­те­лей. Фи­зи­ка ус­ко­ри­те­лей вклю­ча­ет в се­бя во­про­сы, свя­зан­ные с по­луче­ни­ем, ус­ко­ре­ни­ем и на­ко­п­ле­ни­ем час­тиц в са­мых раз­но­об­раз­ных ти­пах ус­ко­ри­те­лей. Ис­сле­ду­ет­ся ди­на­ми­ка дви­же­ния за­ря­жен­ных час­тиц во внеш­них элек­тро­маг­нит­ных по­лях (ди­на­ми­ка про­доль­но­го дви­же­ния, опи­сы­ваю­щая ус­ко­ре­ние час­тиц, и ди­на­ми­ка по­пе­реч­но­го дви­же­ния, опи­сы­ваю­щая фо­ку­си­ров­ку пуч­ков); изу­ча­ют­ся во­про­сы соз­да­ния эле­мен­тов маг­нит­ных и ус­ко­ряю­щих струк­тур (вклю­чаю­щие эле­мен­ты фи­зики сверх­про­во­ди­мо­сти) и эф­фек­ты про­стран­ст­вен­но­го за­ря­да (вклю­чаю­щие взаи­мо­дей­ст­вие час­тиц с эле­мен­та­ми ус­ко­ри­те­ля и друг с дру­гом, в т. ч. со встреч­ным пуч­ком). К фи­зи­ке ус­ко­ри­те­лей от­но­сят­ся так­же изу­че­ние син­хро­трон­но­го из­лу­че­ния, по­лу­че­ние и ус­ко­ре­ние по­ля­ри­зо­ван­ных пуч­ков, фи­зи­ка и тех­ни­ка ох­ла­ж­де­ния пуч­ков, тех­ни­ка по­лу­че­ния вы­со­ко­го ва­куу­ма и взаи­мо­дей­ст­вие пуч­ков с ос­та­точ­ным га­зом в ка­ме­ре ус­ко­ри­те­ля, во­про­сы ра­ди­ац. безо­пас­но­сти и др.

Во­про­сы фи­зи­ки и тех­ни­ки ус­ко­ри­те­лей об­су­ж­да­ют­ся в хо­де ря­да ре­гу­ляр­но про­во­ди­мых кон­фе­рен­ций. Пер­вая ме­ж­ду­нар. кон­фе­рен­ция по У. з. ч. со­стоя­лась в 1956 в ЦЕРНе. На­чи­ная с 1997 ма­те­риа­лы 18 разл. кон­фе­рен­ций пуб­ли­ку­ют­ся в элек­трон­ном ви­де на сай­те http://jacow.org. Круп­ней­шая из них – IPAC (International Particle Accelerator Conference, Ме­ж­ду­нар. кон­фе­рен­ция по ус­ко­ре­нию час­тиц) про­во­дит­ся еже­год­но и со­би­ра­ет ок. 2000 уча­ст­ни­ков. В Рос­сии ре­гу­ляр­но ор­га­ни­зу­ют­ся две ме­ж­ду­нар. кон­фе­рен­ции, по­свя­щён­ные фи­зи­ке и тех­ни­ке ус­ко­ри­те­лей, – Рос. кон­фе­рен­ция по ус­ко­ри­те­лям час­тиц и Ме­ж­ду­нар. се­ми­нар по про­бле­мам ус­ко­ри­те­лей за­ря­жен­ных час­тиц па­мя­ти В. П. Са­ран­це­ва.

41. Эффект Холла.

Эффект Холла относится к группе гальваномагнитных явлений и заключается в том, что под действием магнитного поля, перпендикулярного к электрическому току, электроны в материале отклоняются перпендикулярно как направлению электрического тока, так и магнитного поля. С помощью эффекта Холла стало возможным понять суть процессов проводимости в полупроводниках и провести грань между полупроводниками и другими типами плохо проводящих материалов. Это обусловлено тем, что измерение ЭДС (разности потенциалов) Холла, возникающей в материале перпендикулярно направлению электрического тока и внешнего магнитного поля, дает возможность непосредственно определить концентрацию и знак носителей заряда. Последнее позволяет определить принадлежность материала к тому или иному типу полупроводников (p или n–типа). Измерения эффекта Холла дают возможность отделить случай ионной проводимости от случая электронной проводимости. Наличие эффекта Холла в проводниках и полупроводниках свидетельствует об электронном характере проводимости. С помощью эффекта Холла возможно получить данные и о подвижности носителей заряда (так называемая «холловская» подвижность). Таким образом, можно считать, что эффект Холла – один из наиболее эффективных методов исследования электрических свойств полупроводниковых материалов.

Этот эффект был открыт Е.Холлом в 1879 г.. Сущность явления заключается в следующем. Если металлическую или полупроводниковую пластину, по которой проходит ток, поместить в магнитное поле, направленное перпендикулярно линиям тока (рис.5), то в ней возникает разность потенциалов в направлении перпендикулярном току и магнитному полю.

В основе эффекта лежит взаимодействие между электрическими зарядами и магнитными полями. Любая заряженная частица, движущаяся в магнитном поле, испытывает действие силы Лоренца, направление которой перпендикулярно направлению движения частицы и направлению магнитного поля. Величина этой силы прямо пропорциональна величине заряда q, скорости частицыv и индукции магнитного поля:

(0.1)

Для металлов и для полупроводников n-типа q = -|e|, где |e|— модуль заряда электрона.

Модуль векторного произведения:

(0.2)

У

Рис. 5. Схема возникновения эффекта Холла в полупроводнике n-типа.

с 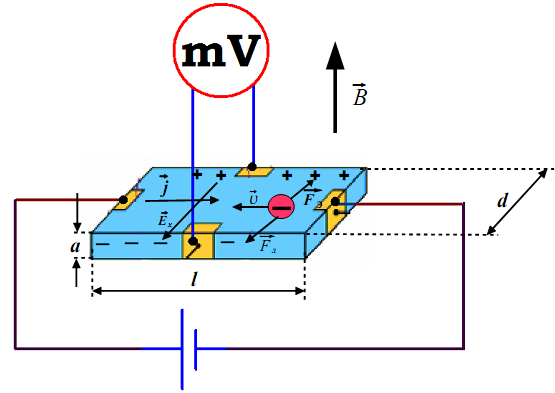ловимся, что магнитное поле направлено строго перпендикулярно вектору скорости частиц . Т. е. угол α между векторами   и   равен 90⁰, а sin(90⁰)=1 Тогда:

 (1)

Под действием силы Лоренца электроны отклоняются к ближней боковой грани пластины рис. 5 и заряжают ее отрицательно. На противоположной грани остается нескомпенсированный положительный заряд ионов кристаллической решетки. В результате этого в пластине возникает поперечное электрическое поле  , направленное от дальней боковой грани к ближней. Обозначим напряженность образовавшегося электрического поля через  . Сила   , действующая со стороны электрического поля на заряд, направлена в сторону, противоположную направлению силы Лоренца   (рис. 5). Возникшая вследствие этого поперечная разность потенциалов U_x называется ЭДС Холла.

Разделение зарядов в образце продолжается до тех пор, пока силы магнитного  и электрического  полей не уравновесят друг друга, т. е.:

 (2)

Откуда находим:

 (3)

Считаем поле   , образовавшееся в пластинке однородным. Тогда находим:

 →   (4)

где d – толщина пластинки в направлении поля E_x (рис. 5).

С учетом выражения (3) получаем, что:

(5)

Сила тока, протекающего через единицу поверхности образца, т. е. плотность тока, равна:

 (5.1)

А модуль выражения (5.1) найдем как:

 (5.2)

где n – число носителей тока в единице объема образца (концентрация носителей тока).

С другой стороны, модуль вектора плотности тока  определяется как , где S – площадь поперечного сечения пластины, перпендикулярная направлению . Тогда:

(5.3)

где а— ширина пластины в направлении вектора рис. 5.

Сопоставляя формулы (5.2) и (5.3), находим:

(5.4)

Выражая из (5.4) скорость электронов v, находим:

(6)

Подставив (6) в (5), получим:

(7)

Обозначим  гдеR_х - постоянная или коэффициент Холла. (Условно считают, что знак постоянной Холла совпадает со знаком заряда носителей тока. У электронных полупроводников постояннаяRотрицательна, у дырочных - положительна, гдеp– концентрация дырок).

Тогда выражение (7) записывается в виде:

(8)

Таким образом, ЭДС Холла зависит от величины проходящего тока, индукции магнитного поля, ширины пластины и концентрации носителей заряда. Зависимость от концентрации говорит о том, что в металлах ЭДС Холла по сравнению с полупроводниками намного меньше, и поэтому использование эффекта Холла началось только с применением полупроводников.

При выводе формулы для U мы полагали, что все носители заряда имеют одинаковую скорость. Если учитывать распределение носителей заряда по скоростям, то необходимо ввести числовой множительA,отличный от единицы:



где А– постоянная, зависящая от механизма рассеяния носителей заряда:А=1,93 … 0,99. Практически для большинства металлов можно считать A≈1.

При рассеянии электронов на тепловых колебаниях решетки:



Откуда получаем:

, (8.1)

Наглядная иллюстрация эффекта Холла в полупроводниках c n-типом и p-типом проводимости приведена на рис. 6 a), б). По сравнению с рисунком 5 здесь пластина повернута на угол  к наблюдателю вокруг оси .

Рис. 6. Эффект Холла в полупроводниках с n-проводимостью а) и p-проводимостью б)

42. Электромагнитная индукция. Опыты Фарадея. Закон Ленца. Вывод закона электромагнитной индукции из закона сохранения энергии.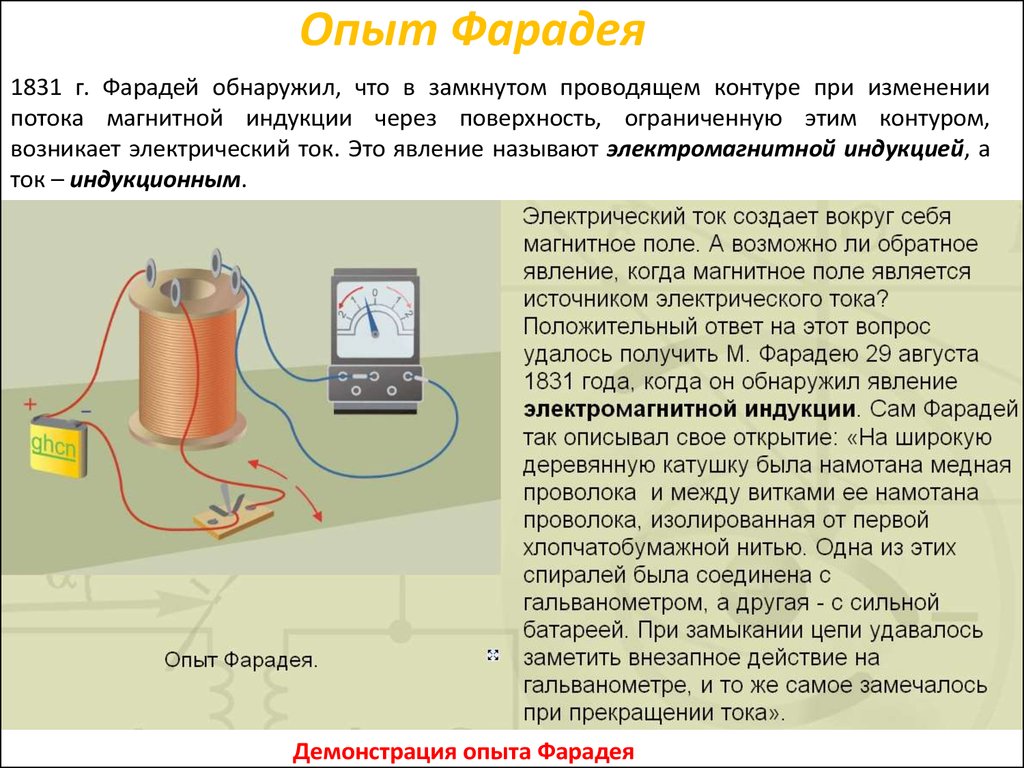



Явление электромагнитной индукции

Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

Опыты Фарадея

• 
  На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
  
• 
  Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
  
• 
  Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.
  

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.

Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Объяснения возникновения индукционного тока

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.

Свойства вихревого электрического поля:

• 
  источник – переменное магнитное поле;
  
• 
  обнаруживается по действию на заряд;
  
• 
  не является потенциальным;
  
• 
  линии поля замкнутые.
  

Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.

Магнитный поток

Магнитным потоком через площадь ​S​ контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ​B​, площади поверхности ​S​, пронизываемой данным потоком, и косинуса угла ​α​ между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):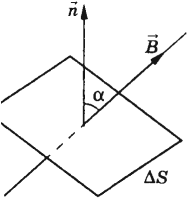





Обозначение – ​Φ​, единица измерения в СИ – вебер (Вб).

Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м², расположенную перпендикулярно вектору магнитной индукции:



Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ​α​ магнитный поток может быть положительным (α < 90°) или отрицательным (α > 90°). Если α = 90°, то магнитный поток равен 0.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Закон электромагнитной индукции Фарадея

Закон электромагнитной индукции (закон Фарадея):

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:



Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ​N​ витков, то ЭДС индукции:



Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ​R​:



При движении проводника длиной ​l​ со скоростью ​v​ в постоянном однородном магнитном поле с индукцией ​B⃗ ​ ЭДС электромагнитной индукции равна:



где ​α​ – угол между векторами ​B⃗ ​ и v⃗ .

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

• 
  магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
  
• 
  вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
  

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

• 
  в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
  
• 
  в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
  

Правило Ленца

Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Алгоритм решения задач с использованием правила Ленца:

• 
  определить направление линий магнитной индукции внешнего магнитного поля;
  
• 
  выяснить, как изменяется магнитный поток;
  
• 
  определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
  
• 
  по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
  

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Энергия магнитного поля

При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.

Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле: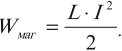



Основные формулы раздела «Электромагнитная индукция»



Алгоритм решения задач по теме «Электромагнитная индукция»:

1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.

2. Записать формулу:

• 
  закона электромагнитной индукции;
  
• 
  ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
  

3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.

4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).

5. Решить полученную систему уравнений относительно искомой величины.

6. Решение проверить.